Published on February 14, 2025 2:29 PM GMT
I recently messed about with Celtic knot patterns, for which there are some fun generators online, eg. https://dmackinnon1.github.io/celtic/ or https://w-shadow.com/celtic-knots/. Just as addictive to doodle as the 'cool s' (https://en.wikipedia.org/wiki/Cool_S) but with more cool.
However, everyone knows that its cooler to tile a plane with hexagons than squares. So I cooked up some tiles to make the Hex-grid equivalent of a Celtic Knot.

These tiles fit to make nice patterns. I think they look vaguely Arabic, and remind me strongly of the game Tsuro. (By the way, I would much prefer that game if the theme was some Italian fairies skate-boarding along the strands of spaghetti, it would fit the chaotic, sabotage heavy gameplay better than the wise Chinese dragon.)

The edges are weird. I want to tile the edges with something like this (below), but that leaves "corners" that are not dealt with as above.
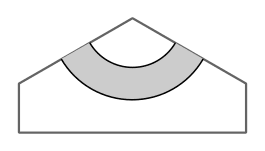
One option is to tile 3 edges with the tile above, and the other three edges (alternating) with the one below
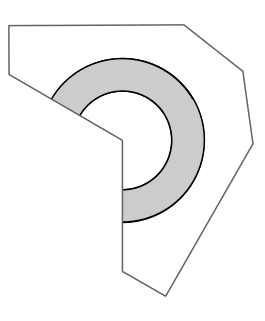
which gives something like this (adding minor embellishments to the "curls" that were crying out for a rod).
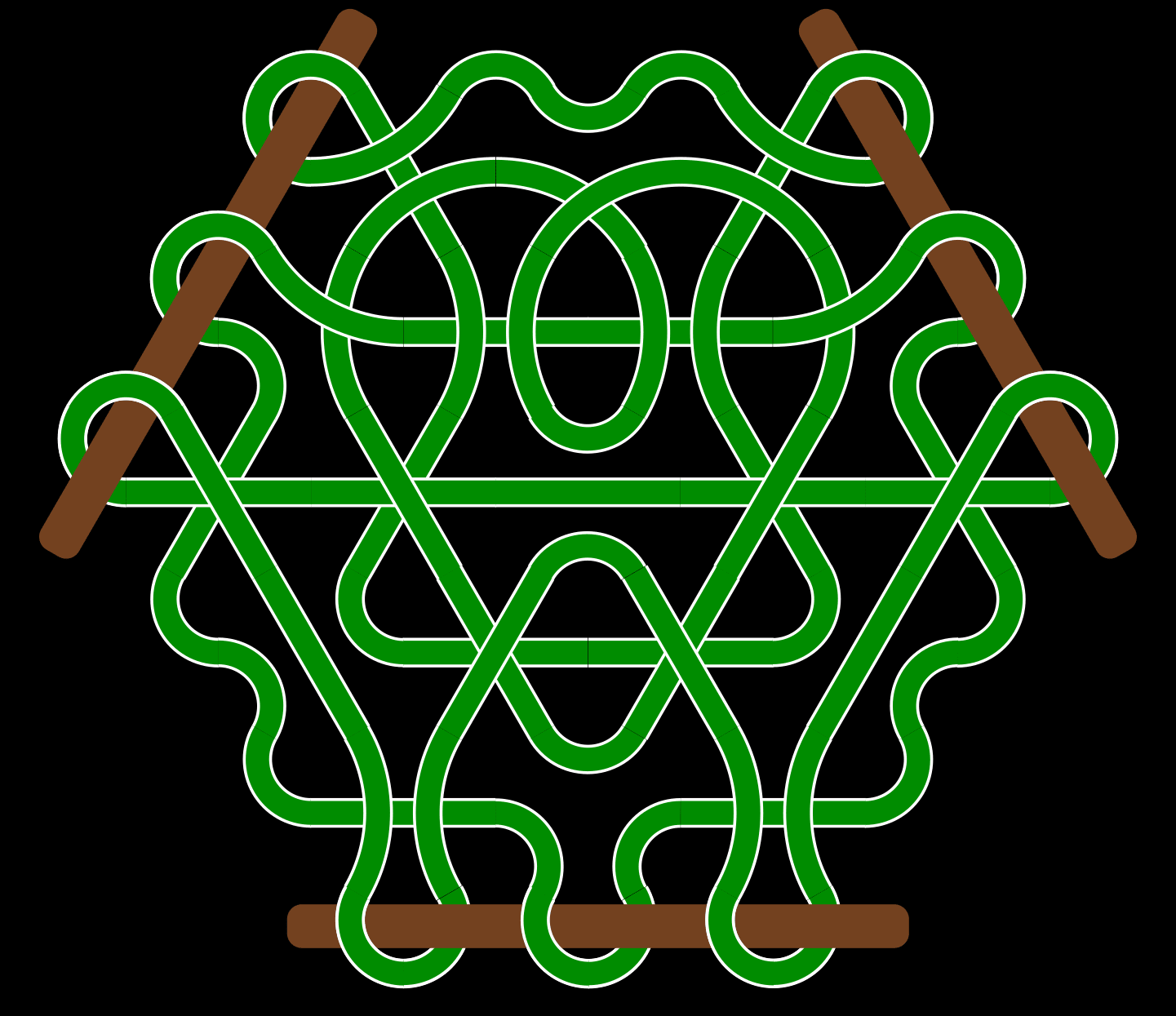
I am still not happy with the edges. I would rather have all three dealt with using the first (simpler looking) unit, then do something at the corners. Mathematics doesn't want to let me do that while pairing up the cords (a "corner hexagon" has 3 unmatched edges, unlike corner squares which have only 2. 2 loose ends can be paired up, but 3 obviously can't.)
What if I wasn't using strings (the ends of which match pairwise) but some hypothetical, Escher-like thing that had "ends" which annihilated in triples? Even if such a shape exists outside bizarre dreams and drug trips, then it would deal with the corners, but break the edges.
Why do the edges annoy me so much? Because I like symmetry. With hexes we can do snowflake symmetry:

Well, almost. Sometimes one line has to go over another. We have unmatched ends at the corners, but using the other edge condition (with loops on alternating sides) would break the symmetry horribly.
Colouring in the one above,

its almost pretty. Maybe not awful for a carpet.
A thicker path usually looks a bit better (this seems to also apply for normal Celtic knots). Each hex tile has some combination of straights (connecting opposite sides of the hex), corners (connecting adjacent sides) and arcs (connecting sides neither opposite nor adjacent). I think patterns making heavy use of arcs look best.

Leaving the edges alone entirely (as above) looks unfinished, which I think is possibly nicer than the normal situation where the edges look like they have been finished badly.
We can't tile a ball with hexagons, so we can't get out of our boundary problem by working on those. (Ball-tiling requires some pentagons, which is an issue, because 5 sided shapes means loose ends). We could roll up our "graphene like" sheets into carbon nanotubes, basically just periodic boundaries on one side, not very interesting, and still breaking our 6 fold symmetry. A torus would also break the symmetry but is possibly cool enough to get away with it.
If anyone wants to mess with this my odds and ends (eg the tiles) are in this folder as inkscape .svg images : https://drive.google.com/drive/folders/1BS42moNocDLIwFGeEAESK0ttX4CANo-5?usp=sharing
Discuss

