


论文题目:Gauge Invariance of Equilibrium Statistical Mechanics
论文地址:https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.133.217101
期刊名称:Physical Review Letters
近日,德国拜罗伊特大学的研究团队发表了一项重要成果,揭示了平衡统计力学中一个全新的对称性——规范不变性。研究表明,这种对称性深刻地影响了统计力学的理论基础,并有望为计算方法的优化和新理论工具的开发提供启示。这项突破性研究不仅加深了我们对统计力学的理解,也为实验和模拟技术的结合开辟了新的途径。
研究的核心是通过对经典相空间的“移位操作”进行研究,发现这一操作实际上是一种局域规范变换。规范变换的特性在于,它不会改变任何物理可观测量。这种对称性在理论上表现为一个非交换的李代数结构,并且可以通过热平均导出一系列精确的统计力学求和规则。研究团队通过数值模拟证明,这种变换对平衡态物理量不会产生任何影响,从而证实了这一理论的规范不变性。
传统的统计力学主要通过哈密顿量和配分函数来描述体系的性质,而新研究引入的规范变换则提供了一种新的视角。通过引入局域移位操作,研究者能够从微观动力学出发,系统性地构建统计力学中的精确关系式。这一框架不仅统一了已有的一些理论结果,还揭示了新规则之间的内在联系。例如,研究表明,通过这种操作可以生成与空间相关的高阶关联函数,从而更加深入地刻画粒子间的相互作用。
研究团队采用蒙特卡洛模拟对其理论进行了验证,特别是在一维硬棒模型和软势系统(如Lennard-Jones势)的场景下。在这些模拟中,粒子的位移和动量被重新分布,但最终的平衡态分布与初始系统保持完全一致。这种数值验证不仅巩固了理论框架的可靠性,也展示了其在实际计算中的可行性。
这一研究的潜在应用非常广泛。例如,粒子系统中的力采样算法可以通过这一框架进一步优化。此外,最近基于显微镜技术的局域力测量方法,也有望与这一理论结合,从实验层面验证其准确性和适用性。同时作者也提出了许多未解的问题。例如,规范变换是否可以推广到更一般的动力学系统?其与非平衡态统计力学的关系如何?这些问题的解答将进一步推动这一领域的发展。
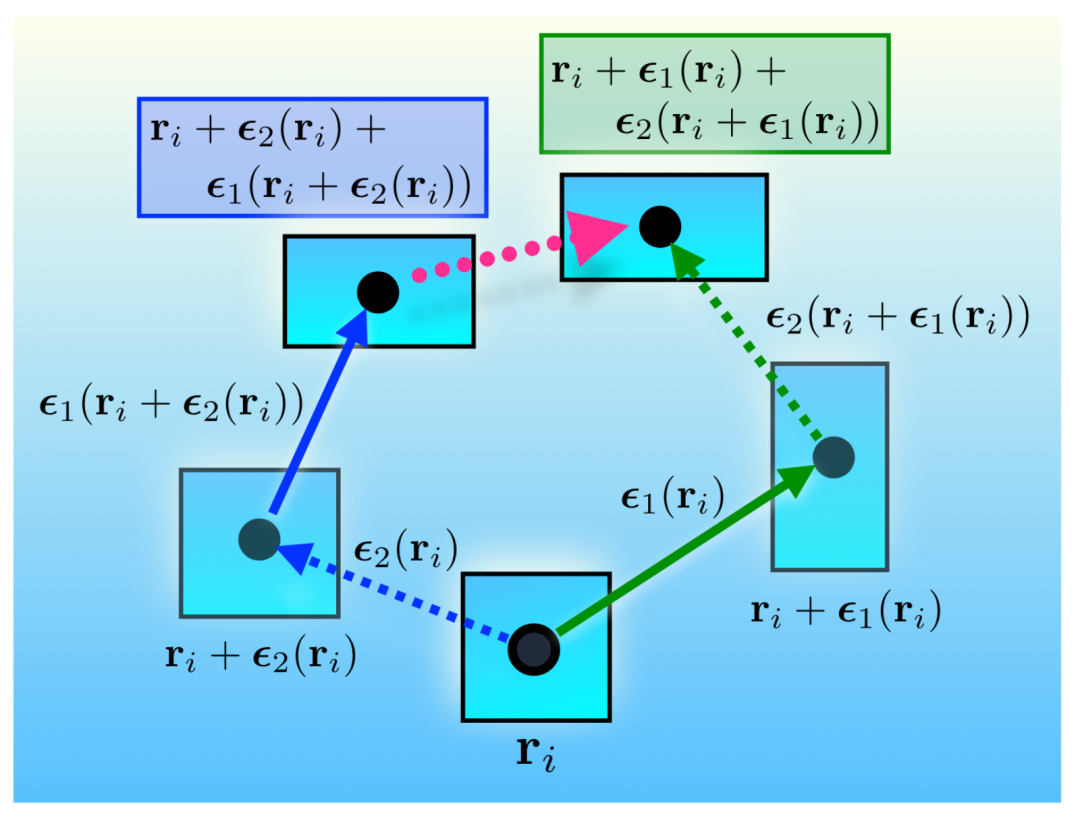
图1. 相空间位移的非交换性
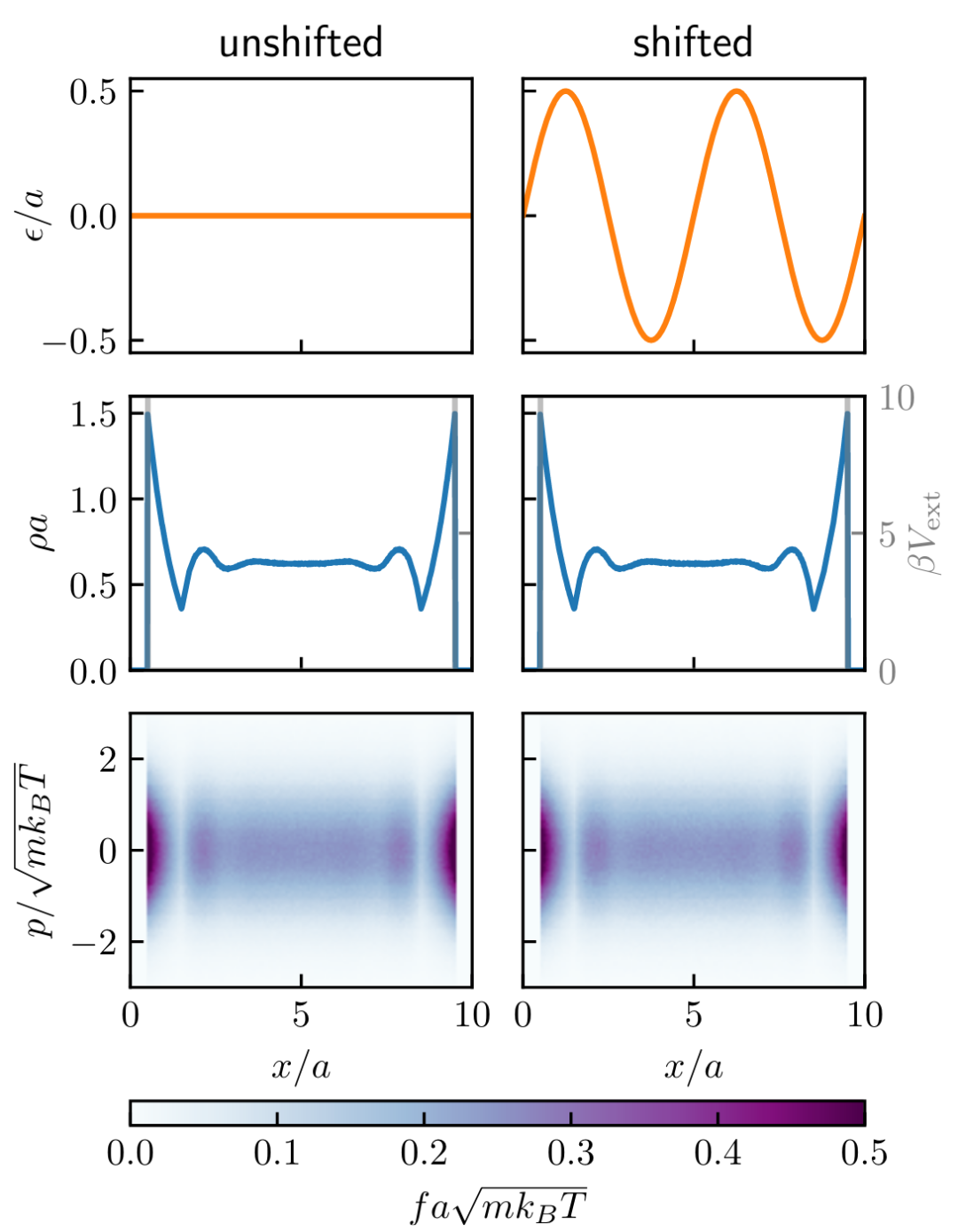
图2. 限制在间隔距离 L = 10a 的两个硬壁之间的一维硬杆的蒙特卡罗结果
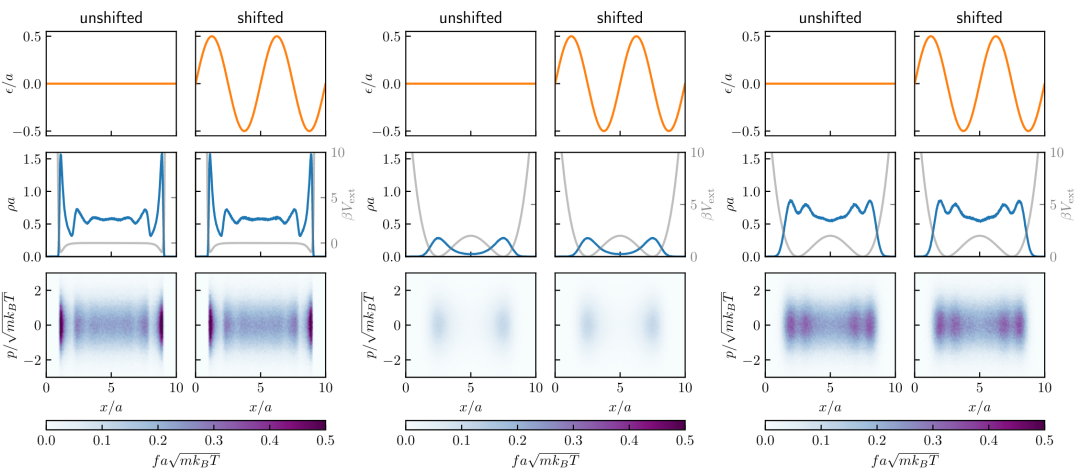
图3. Lennard-Jones 粒子规范不变性的计算机模拟结果
龚铭康 | 编译
非平衡统计物理读书会启动!

详情请见:从热力学、生命到人工智能的统计物理之路:非平衡统计物理读书会启动!
6. 加入集智,一起复杂!

