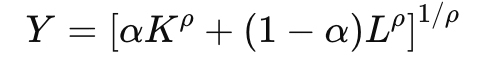Published on April 4, 2025 5:41 PM GMT
Epistemic status – thrown together quickly. This is my best-guess, but could easily imagine changing my mind.
Intro
I recently copublished a report arguing that there might be a software intelligence explosion (SIE) – once AI R&D is automated (i.e. automating OAI), the feedback loop of AI improving AI algorithms could accelerate more and more without needing more hardware.
If there is an SIE, the consequences would obviously be massive. You could shoot from human-level to superintelligent AI in a few months or years; by default society wouldn’t have time to prepare for the many severe challenges that could emerge (AI takeover, AI-enabled human coups, societal disruption, dangerous new technologies, etc).
The best objection to an SIE is that progress might be bottlenecked by compute. We discuss this in the report, but I want to go into much more depth because it’s a powerful objection and has been recently raised by some smart critics (e.g. this post from Epoch).
In this post I:
- Explain an intuitive version of the compute bottleneck objection, and a more precise ‘economist version’ of the objectionGive a long list of reasons why I don’t find this ‘economist version’ of the objection convincing. I argue that the substitutability between cognitive labor and compute is likely higher in AI R&D than in economic estimates of the substitutability between inputs in other fieldsConclude that there’s a good chance that compute bottlenecks don’t slow an SIE until its late stages
The compute bottleneck objection
Intuitive version
The intuitive version of this objection is simple. The SIE-sceptic says:
Look, ML is empirical. You need to actually run the experiments to know what works. You can’t do it a priori. And experiments take compute. Sure, you can probably optimise the use of that compute a bit, but past a certain point, it doesn’t matter how many AGIs you have coding up experiments. Your progress will be strongly constrained by your compute.
An SIE-advocate might reply: sure, we’ll eventually fully optimise experiments, and past that point won’t advance faster. But we can maintain a very fast pace of progress, right?
The SIE-sceptic replies:
Nope, because ideas get harder to find. You’ll need more experiments and more compute to find new ideas over time, as you pluck the low-hanging fruit. So once you’ve fullu optimised your experiments your progress will slow down over time. (Assuming you hold compute constant!)
Economist version
That’s the intuitive version of the compute bottlenecks objection. Before assessing it, I want to make what I call the “economist version” of the objection. This version is more precise, and it was made in the Epoch post.
This version draws on the CES model of economic production. The CES model is a mathematical formula for predicting economic output (GDP) given inputs of labour L and physical capital K. You don’t need to understand the math formula, but here it is:
The formula has a substitutability parameter ρ which controls the extent to which K and L are complements vs substitutes. If ρ<0, they are complements and there’s a hard bottleneck – if L goes to infinity but K remains fixed, output cannot rise above a ceiling. (There’s also a parameter α but it’s less important for our purposes. α can be thought of as the fraction of tasks performed by L vs K. I’ll assume α=0.5 throughout.)
Here are the predictions of the CES formula when K=1 and ρ = -0.2.
This graph shows the implications of a CES production function. It shows how output (Y) changes when K=1 and L varies, with ρ = -0.2. The blue line shows output growing with more labor but approaching the red ceiling line, demonstrating the maximum possible output when K=1.
We can apply the CES formula to AI R&D during a software intelligence explosion (SIE). In this context, L represents the amount of AI cognitive labour applied to R&D, K represents the amount of compute, and Y represents the pace of AI software progress. The model can predict how much faster AI software would improve if we add more AGI researchers but keep compute fixed.
In this context, the ‘ceiling’ gives the max speed of AI software progress as cognitive labour tends to infinity but compute is held fixed. A max speed of 100 means progress could become 100 times faster than today, but no faster, no matter how many AGI researchers we add, and no matter how smart they are or how quickly they think.
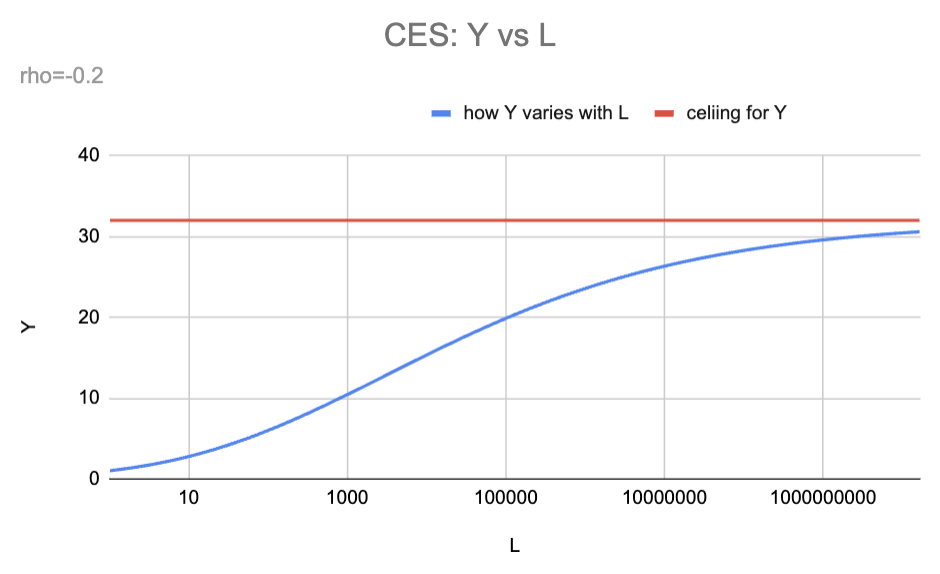
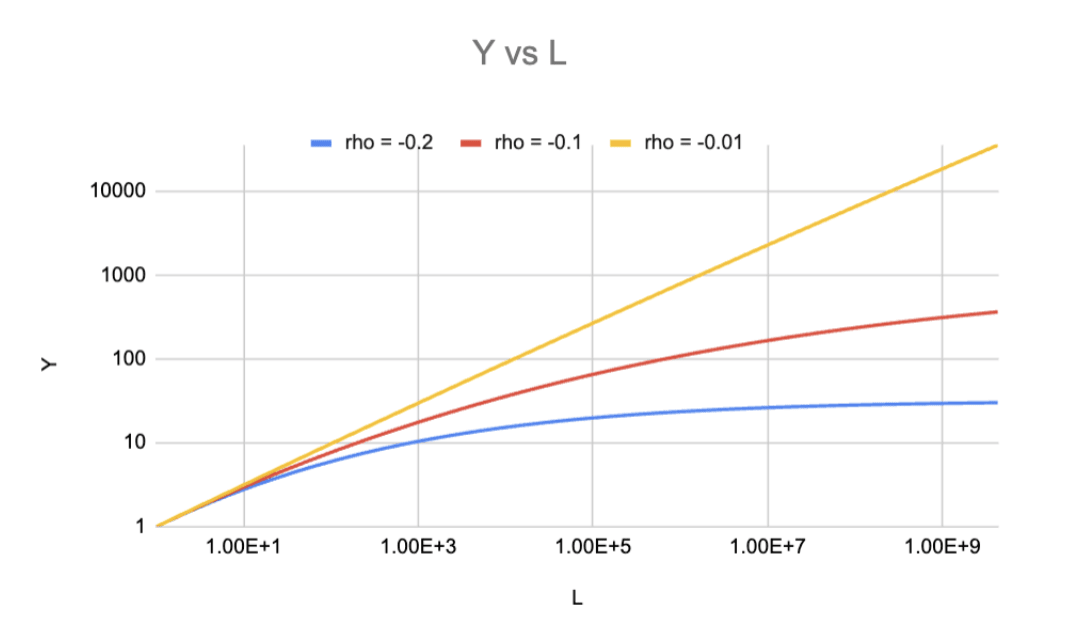
Here is the same diagram as above, but re-labelled for the context of AI R&D:
This graph applies the CES model to AI research. The blue line shows how the pace of progress would change if compute is held fixed but cognitive labour increase. With ρ = -0.2, progress accelerates with more automated researchers but approaches a maximum of ~30× current pace.
As the graph shows, the CES formula with ρ = -0.2 implies that if today you poured an unlimited supply of superintelligent God-like AIs into AI R&D, the pace of AI software progress would increase by a factor of ~30.
Once this CES formula has been accepted, we can make the economist version of the argument that compute bottlenecks will prevent a software intelligence explosion. In a recent blog post, Epoch say:
If the two inputs are indeed complementary [ρ<0], any software-driven acceleration could only last until we become bottlenecked on compute…
How many orders of magnitude a software-only singularity can last before bottlenecks kick in to stop it depends crucially on the strength of the complementarity between experiments and insight in AI R&D, and unfortunately there’s no good estimate of this key parameter that we know about. However, in other parts of the economy it’s common to have nontrivial complementarities, and this should inform our assessment of what is likely to be true in the case of AI R&D.
Just as one example, Oberfield and Raval (2014) estimate that the elasticity of substitution between labor and capital in the US manufacturing sector is 0.7 [which corresponds to ρ=-0.4], and this is already strong enough for any “software-only singularity” to fizzle out after less than an order of magnitude of improvement in efficiency.
If the CES model describes AI R&D, and ρ=-0.4, then the max speed of AI software progress is 6X faster than today (continuing to assume α=0.5). So an SIE could never become that fast to begin with. And once we do approach the max speed, diminishing returns will cause progress to slow down. (I’m not sure where they get their “less than an order of magnitude” claim from, but this is my attempt to reconstruct the argument.)
Epoch used ρ = -0.4. What about other estimates of ρ ? I’m told that economic estimates of ρ range from -1.2 to -0.15. The corresponding range for max speed is 2 - 100:
Max speed of AI software progress (holding compute fixed, with as cognitive labour tends to infinity) | |
| -1 | 2 |
| -0.5 | 4 |
| -0.2 | 32 |
| -0.15 | 102 |
| -0.1 | 1024 |
| 0 (Cobb Douglas) | inf |
Let’s recap the economist version of the argument that compute bottlenecks will block an SIE. The SIE-skeptic invokes a CES model of production (“inputs are complementary”), draws on economic estimates of ρ from the broader economy, applies those same ρ estimates to AI R&D, notices that the max speed for AI software progress is not very high even before diminishing returns are applied, and conclude that an SIE is off the cards.
That’s the economist version of the compute bottlenecks objection. Compared to the intuitive version, it has the advantage of being more precise, (if true) more clearly devastating to an SIE, and the objection recently made by Epoch. So i’ll focus the rest of the discussion on the economist version of the objection.
Counterarguments to the compute bottleneck objection
I think there are lots of reasons to treat the economist calculation here as only giving a weak prior on what will happen in AI R&D, and lots of reasons to think ρ will be higher for AI R&D (i.e. compute will be less of a bottleneck than the economic estimates suggest).
Let’s go through these reasons. (Flag: I’m giving these reasons in something like reverse order of importance.)
- Standard empirical difficulties. Empirical estimates of ρ are generally messy and hard to get right. There are identification problems, confounders, data measurement issues, etc.
- Takeaway: put less weight on economic estimates of ρ.
- Indeed, Cobb Douglas is a good model for long-run growth, and in Cobb Douglas ρ=0. Jones (2003) ventures an interesting hypothesis to explain this. Jones’ hypothesis is that in the short run we can’t effectively use an influx of labour without getting bottlenecked by limited physical capital, so is low. But in the longer run we invent new production processes that use our new balance of inputs more effectively, and so ρ is higher. In his model, ρ=0 in the long-run case. Think of it like this: if you suddenly had twice as many workers but the same amount of factory equipment, initially they'd get in each other's way. But over time, you'd reorganize the factory to make better use of all those workers, reducing the bottleneck effect. We can apply Jones’ hypothesis to the context of AI R&D. In this context, it means that if we had a an influx millions of AGIs, then initially the pace of AI progress wouldn’t speed up that much (and the compute bottleneck objection would hold); but that once we’d found a way to reconfigure AI R&D to make good use of that abundant cognitive labour, there wouldn’t be a hard bottleneck (ρ=0) and we’d get an SIE. Importantly, that reconfiguration could be very quick with fast-thinking AGIs! Rather than taking years or decades, it could happen in days or weeks. In which case, we might simply observe that ρ is close to 0.As a very toy example (i think credit to Ryan Greenblatt), in the limit of infinite AGIs you could use AGIs to do the math for NNs in their heads and thereby fully simulate computational experiments using cognitive labour in place of compute. Obviously this won’t be feasible in practice, but it does mean that the ρ<0 is flawed in the absolute limit. Cognitive labour can in principle fully substitute for compute! Takeaway: take values of ρ right next to 0 comparably seriously as ones in the estimated range.
- Takeaway: be very wary of using these estimates in the context of an SIE!
The SIE involves inputs of cognitive labour rising by multiple orders of magnitude. But empirical measurements of ρ span a much smaller range, making extrapolation very dicey.
Points 1-3 are background, meant to warm readers up to the idea that we shouldn’t be putting much weight on economic ρ estimates in the context of AI R&D, and suggesting that values very close to 0 are similarly plausible to the values found by economic studies. Now I’ll argue more directly that ρ should be closer to 0 for AI R&D.
- Economic estimates don’t include labourers becoming smarter or thinking faster. The empirical estimates look at empirical variation in the ratio of labour to capital, L/K – they account for “more workers” but not “smarter workers”. This is a very big drawback when applying them to the case of an SIE. R&D is very cognitively loaded – smarts help a lot. And the core dynamic of the SIE is that AI is becoming smarter over time (though I expect getting more parallel copies to also play an important role). Economic estimates of ρ don’t speak to that dynamic at all.
- An upcoming post from Eli Lifland and Dan Kokotajlo surveys 8 AI researchers, who guess that moving from “all researchers as good as median employee” to “all researchers as good as the top employee” would increase pace of AI progress by a factor of 6 (median estimate), suggesting that “smarter researchers” is a very big effect within the range of top human experts.Similarly the economic estimates don’t speak to the effects of AI thinking speed increasing during an SIE.Takeaway: raise our estimate of ρ. I’d expect the gains from “more, smarter, faster workers” to be less bottlenecked than the benefits from just “more workers”.
- A smart SIE-sceptic might reply: Ah, but that only shows you can run more experiments at a fixed capability level. What really matters is the number of ‘near-frontier’ experiments: experiments close in size to the largest training runs, e.g. experiments that use 1% of the lab’s compute. And the number of near-frontier experiments is fixed. But this reply isn’t convincing. Firstly, you might not need near-frontier experiments. You might instead be able to extrapolate from experiments that use increasingly small fractions of the lab’s compute. Secondly, the argument proves too much. Over the past ten years, the number of near-frontier experiments that the world has been able to run has significantly decreased! Training run size has grown much faster than the world’s total supply of AI compute. If these near-frontier experiments were truly a bottleneck on progress, AI algorithmic progress would have slowed down over the past 10 years.Takeaway: raise our estimate of ρ. (Or keep ρ the same, but replace ‘compute’ with ‘# experiments’, which will weaken the case against SIE.)
- Wait, where are my claims about max speed coming from? Reasoning about the max speed could be its own post. But my views here are informed by thinking through, and talking to AI researchers about, the specific things you could do with abundant cognitive labour, like: running smaller scale experiments, optimising every part of the stack, generating way better ideas for new algorithms/paradigms, designing way better experiments, stopping experiments early wherever possible, etc.
- See here for more detail, and also see the upcoming takeoff speeds post from Eli Lifland and Dan Kokotajlo.And notice that these things mostly don’t really have clear analogues in the case of manufacturing (where the economics estimates are from). If you’re running a washing machine factory, “optimising every part of the stack” will just have much smaller gains than in AI, and there’s no clear analogue to ‘running smaller scale experiments’. So again, we shouldn’t be surprised if estimates from manufacturing overestimate bottlenecks.
- (I do think there’s a viable route here for an SIE-sceptic to simply bite the bullet and argue that the max speed is not that high – seems worth exploring.)
- This brings us back to Chad Jones’ explanation for why long-term ρ is very close to 0 – we adjust our method of production to whichever option makes the best use of super abundant cognitive labour.
Taking stock
Ok, so let’s take stock. I’ve given a long list of reasons why I find the economist version of the compute bottleneck objection unconvincing in the context of a software intelligence explosion (SIE), and why I expect ρ to be higher than economics estimates.
So I feel confident that our SIE forecasts should be more aggressive than if we naively followed the methodology of using economic data to estimate ρ. But how much more aggressive?
Our recent report on SIE assumed ρ = 0, which I think is likely a bit too high. In particular, I suggested above that the most likely range for ρ is between -0.2 and 0. As shown by the following graph, the difference between -0.2 and 0 doesn’t make a big difference in the early stages of an SIE (when total cognitive labour is 1-3 OOMs bigger than the human contribution), but makes a big difference later on (once total cognitive labour is >=5 OOMs bigger than the human contribution).
Sensitivity analysis on values of ρ. Within the range -0.2 < ρ < 0, the predictions of CES don’t differ significantly until labour inputs have grown by ~5 OOMs. If this is the range of ρ for AI R&D, compute bottlenecks won’t bite in the early stages of the SIE.
This suggests that compute bottlenecks are unlikely to block an SIE in its early stages, but could well do so after a few OOMs of progress. Of course, that’s just my best guess – it’s totally possible that compute bottlenecks kick in much sooner than that, or much later.
In light of all this, my current overall take on the SIE is something like:
- Absent a hard compute bottleneck – i.e. assuming ρ = 0 – it looks like returns to AI software R&D are comfortably good enough for an SIE. And indeed, it’s plausible that there’s no such hard bottleneck. So an SIE is plausible. But it’s also plausible that there is a hard compute bottleneck – ρ < 0. If so, it might only have a big effect once we’re many OOMs into the SIE (if -0.2 < ρ < 0), or it might kick in sooner (if ρ < -0.2, as in most economic estimates). Digging into all this more is one of the most important things for better understanding the prospects for an SIE (with the other contender being researching how far an SIE could go before reaching effective physical limits). Again, this is all very complicated and tricky stuff! I could imagine changing my mind on this on the basis of further research.
It’s hard to know if I actually disagree with Epoch on the bottom line here. Let me try and put (very tentative) numbers on it! I’ll define an “SIE” as “we can get >=5 OOMs of increase in effective training compute in <1 years without needing more hardware”. I’d say there’s a 10-40% chance that an SIE happens despite compute bottlenecks. This is significantly higher than what a naive application of economic estimates would suggest.
Discuss