关键词：降维 设施选址 近似算法

导  读

本文是对 STOC 2025 会议接收论文 Near-Optimal Dimension Reduction for Facility Location 的解读。论文作者按照姓氏首字母排序，为南京大学副教授黄棱潇，北京大学助理教授姜少峰，魏茨曼科学研究所教授 Robert Krauthgamer 和北京大学本科生岳镝。

这项工作研究如何针对设施选址问题进行降维，以保持降维前后最优值的变化不超过  。论文证明了一个接近最优的目标维数上界，这一降维结果在针对设施选址问题的数据流算法和近似算法中都有直接应用。

← 扫码跳转论文

论文地址：https://arxiv.org/abs/2411.05432

01

问题介绍

降维与内蕴维数

在机器学习、计算几何等领域的研究中，数据通常被表示成欧氏空间  中的向量。多数情况下，计算问题的复杂度指数地依赖于表示的维数  ，这种现象被称为维数灾难（Curse of Dimensionality）。降维（dimension reduction）是一种克服维数灾难的重要技术，即寻求高维点集的低维表示。具体而言，对于高维欧氏空间中的点集  ，人们希望找到一个映射  ，将  映射到低维空间  中，同时保持  和  的性质足够接近。这样一来，只需在低维表示  上解决相应的计算问题，就可得到原问题解的一个估计。著名的 Johnson-Lindenstrauss 引理告诉我们，若要近似保持  中点的两两距离，只需要降到  维即可。

定理 1.1（Johnson-Lindenstrauss 引理 [JL84]）给定  ，  ，存在  和随机映射  ，使得对任意  元点集  ，以概率 0.9 满足 定理 1.1 中，目标维数只依赖于表示精度和点集大小，而与原始空间维数无关。更有趣的是，降维映射  其实是一个简单的高斯矩阵，与输入数据无关（data oblivious）。很不幸，目标维数  对于很多计算问题来说仍然难以承受。这是因为，一方面，定理中  的上界被证明是紧的 [LN17]；另一方面，许多问题的计算复杂性对于维数有双重指数的依赖关系。

为了克服目标维数中  的制约，通常存在两种解决思路。一种思路是寻找目标维数与输入点集内蕴维数（intrinsic dimension）的关系。不难看出，定理 1.1 中目标维数对  的依赖本质上是对输入点集的某种“维数”的依赖，因为基本的线性代数告诉我们，  个向量张成的子空间维数不超过  。事实上，目标维数中的  正好刻画了输入点集的 doubling dimension。

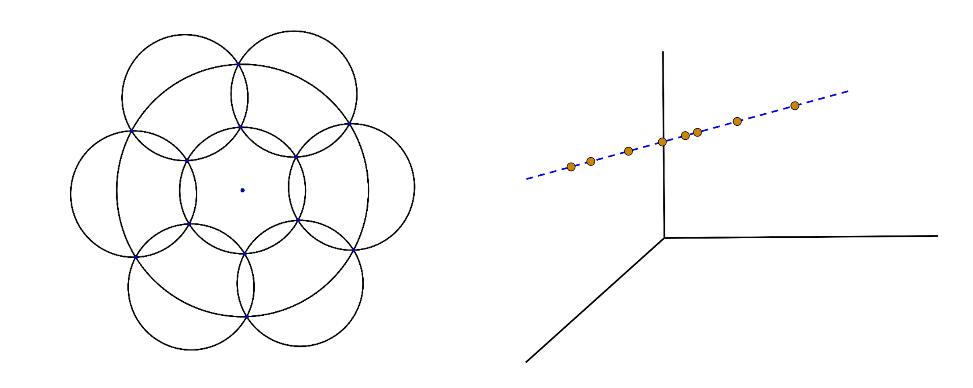
定义 1.2（Doubling dimension [GKL03]）度量空间  的 doubling dimension  是满足如下条件的正实数  的下确界：  ，  中任意一个半径为  的球均能被  个半径为  的球覆盖。

左图：平面上的一个圆能被 7 个半径一半的小圆覆盖；右图：三维空间中的点集排列成一条（一维）直线。

容易验证，  元点集的 doubling dimension 至多是  ；而欧氏空间  的 doubling dimension 是  。在实际应用中，尽管输入点集  有  维的向量表示，但  通常只有常数量级。因此，一个自然的想法是改进定理 1.1 的目标维数，使其只依赖于  。

问题 1.3  给定  ，  ，是否存在  和随机映射  ，使得满足  的任意点集  ，均以概率 0.9 满足 (1)？

这是度量空间研究中的一个著名的开放性问题，至今鲜有进展。

另一种克服目标维数  的思路是针对特定计算问题研究降维。对欧氏空间中的组合优化问题，人们只关心其最优值或最优解在降维后能否被近似地保持。相比保距离，这通常是一个更弱的要求，因此容易得到更低的目标维数。在这项工作中，我们研究针对设施选址问题的降维。

设施选址问题

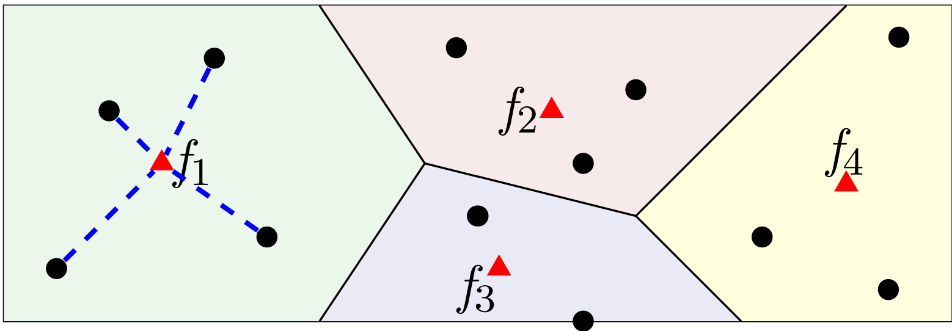
均匀设施选址（Uniform Facility Location）是一个基本的聚类问题。输入（高维）欧氏空间内的点集  和设施单价  ，我们的目标是找到一个设施集合  ，最小化总开销 其中  。(2) 中第一项描述了所有设施的开销（opening cost）；第二项描述了所有数据点到其最近设施的距离总和，通常称为连接开销（connection cost）。记设施选址问题的最优值  。我们关心如下问题：

问题 1.4  给定  ，  ，是否存在  和随机映射  ，使得满足  的任意点集  ，均以概率 0.9 满足 

02

主要结果

针对问题 1.4，我们给出肯定的回答。

定理 2.1  问题 1.4 中，目标维数  ，  为高斯随机矩阵。

此前，对设施选址问题的降维只能做到  -近似最优值，并使用  的目标维数 [NSIZ21]。  -近似和  -近似存在本质区别。在  -近似中，可以不妨假设设施集合  是输入数据集  的子集，容易验证这至多导致总开销增加 2 倍；而  -近似则需要允许  取自整个高维的环境（ambient space），必须引入全新的证明框架和技术。定理 2.1 表明，目标维数  并不依赖于原空间的环境维数  ，而几乎线性依赖于数据本身的内蕴维数  。

结合数据流算法研究中的已知结果，我们得到如下推论：

推论 2.2  存在一个数据流算法，对于输入  ，  ，以及动态增删的数据流  （满足  ），输出对  的  -估计，使用空间 最后，运用类似的技术，我们给出了一个求设施选址问题近似解的随机算法。当  时，其运行时间几乎线性依赖于问题规模。

定理 2.3  存在一个随机算法，输入  和  元点集  ，以常数概率输出关于  的设施选址问题的  -近似解  ，时间复杂度  。其中 在定理 2.3 的设定中，输入数据集  位于高维欧氏空间  中，但  本身有较小的 doubling dimension。另一方面，近似解  却被允许从整个（高维）环境中选取。这种情形介于高维与低维之间，与此前关于设施选址问题的近似算法研究都有所不同。我们相信，这种问题设置能为以后高维计算几何的研究提供新的思路。

参考文献

[GKL03] Anupam Gupta, Robert Krauthgamer, and James R. Lee. Bounded geometries, fractals, and low-distortion embeddings. In FOCS, pages 534–543. IEEE Computer Society, 2003.

[JL84] William Johnson and Joram Lindenstrauss. Extensions of Lipschitz maps into a Hilbert space. Contemporary Mathematics, 26:189–206, 01 1984. doi:10.1090/conm/026/737400.

[LN17] Kasper Green Larsen and Jelani Nelson. Optimality of the johnson-lindenstrauss lemma. In FOCS, pages 633–638. IEEE Computer Society, 2017.

[NSIZ21] Shyam Narayanan, Sandeep Silwal, Piotr Indyk, and Or Zamir. Randomized dimensionality reduction for facility location and single-linkage clustering. In ICML, volume 139 of Proceedings of Machine Learning Research, pages 7948–7957. PMLR, 2021.

图文 | 岳镝

PKU 姜少峰Lab

姜少峰博士，现任北京大学前沿计算研究中心助理教授、北京大学博雅青年学者，于2021年正式加入中心。他于2017年在香港大学获得博士学位，曾在以色列魏茨曼科学研究学院进行博士后研究，并曾在芬兰阿尔托大学任助理教授。他的研究方向为理论计算机科学，近期侧重于大数据算法及其在机器学习中的应用，并已在包括 STOC，FOCS，SICOMP，SODA，ICML，NeurIPS 等主流国际期刊和会议上发表论文多篇。

姜少峰Lab相关科研动态

—   版权声明  —

本微信公众号所有内容，由北京大学前沿计算研究中心微信自身创作、收集的文字、图片和音视频资料，版权属北京大学前沿计算研究中心微信所有；从公开渠道收集、整理及授权转载的文字、图片和音视频资料，版权属原作者。本公众号内容原作者如不愿意在本号刊登内容，请及时通知本号，予以删除。

点“阅读原文”转论文链接

内容中包含的图片若涉及版权问题，请及时与我们联系删除