index_new5.html
../../../zaker_core/zaker_tpl_static/wap/tpl_guoji1.html
![]()
细胞中的蛋白质时空组织对许多重要功能至关重要,而反应-扩散系统描述了细胞膜上的蛋白质动力学与胞质内的扩散过程的相互作用。然而,体-边界耦合现象使得这类系统的计算复杂度极高,尤其是在动态几何结构下。近日发表在Physical Review E的一篇文章提出了一种新的方法,通过将体内的蛋白质浓度梯度投影到细胞膜上,降低计算维度。该方法利用物理信息,用少数主浓度分布特征近似胞质动力学,显著提高了计算速度,尤其在大型系统中表现出色。这种降维框架不仅能捕捉蛋白质在动态几何形态下的自组织行为,还适用于复杂几何耦合的反应扩散系统,为生物物理学研究提供了重要工具。
🤔 **反应-扩散系统描述了细胞膜蛋白质动力学与胞质内扩散过程的相互作用,但体-边界耦合导致计算复杂度高。** 细胞内蛋白质的时空组织对于形态发生、细胞极性建立等重要功能至关重要,而反应-扩散系统正是描述这种蛋白质动力学与胞质内扩散过程相互作用的模型。然而,由于涉及膜与体积两个不同维度的相互作用,体-边界耦合现象使得这类系统的计算变得非常复杂,尤其是在面对动态变化的几何结构时,现有的数值计算工具效率往往较低。
💡 **新方法利用物理信息,将体内的蛋白质浓度梯度投影到细胞膜上,降低计算维度。** 为了解决传统方法忽略胞质内关键浓度梯度的问题,该研究提出了一种新的降维处理方法。该方法通过将体内的蛋白质浓度梯度投影到细胞膜上,有效地降低了计算维度。这种方法类似于有限元法,但更加高效,并且能够在生物学相关系统中保持较高的准确性。
🚀 **该方法显著加快了计算速度,尤其在大型系统中表现出色,并能捕捉蛋白质在动态几何形态下的自组织行为。** 研究表明,这种降维处理框架不仅能很好地捕捉蛋白质在动态几何形态下的自组织行为,还在数值分析中展现出五倍以上的速度提升,特别适用于带有复杂几何耦合的反应扩散系统。这对于研究细胞极性建立、组织形态发生等复杂生物系统具有重要意义。
🧬 **未来该方法可进一步应用于细胞极性建立、组织形态发生等复杂生物系统的建模和分析。** 该方法为生物物理学领域的研究提供了重要的工具,未来可以进一步应用于细胞极性建立、组织形态发生等更复杂的生物系统的建模和分析,推动相关领域的研究发展。
关键词:反应-扩散系统,体-边界耦合,蛋白质动力学,动态几何
论文题目:Dimensionality reduction in bulk-boundary reaction-diffusion systems
论文地址:https://journals.aps.org/pre/abstract/10.1103/PhysRevE.110.034412
期刊名称:Physical Review E
在细胞中,蛋白质的时空组织是许多重要功能的基础,例如形态发生、细胞极性建立等。这些过程主要由细胞膜上的蛋白质动力学与胞质内的扩散过程共同作用来完成,这通常被称为反应-扩散系统。然而,这类系统中的体-边界耦合现象由于涉及两个不同维度的区域(膜与体积)的相互作用,导致其计算复杂度极高,特别是在面对动态变化的几何结构时,现有的数值计算工具效率较低。为了准确预测这些系统中的自组织行为,必须解决膜蛋白和胞质蛋白之间的复杂耦合问题以及其对几何形态的敏感性。然而,传统方法在应对这一问题时,往往忽略了胞质内的关键浓度梯度,导致模型不够精确。
近日发表于 Physical Review E 的一篇文章提出了一种处理体-边界反应扩散系统的新方法。该方法可以将体内的蛋白质浓度梯度投影到细胞膜上,从而降低计算维度。他们利用物理信息,通过少数几个主浓度分布特征对胞质内的动力学进行近似。这一方法类似有限元法,但更加高效,并且能在生物学相关系统中保持较高的准确性。
实验表明,该方法可以显著加快计算速度,尤其是在大体积的系统中表现出色。这种降维处理框架不仅能很好地捕捉蛋白质在动态几何形态下的自组织行为,还在数值分析中展现出五倍以上的速度提升,特别适用于带有复杂几何耦合的反应扩散系统。未来,这一方法可进一步应用于细胞极性建立、组织形态发生等复杂生物系统的建模和分析,为生物物理学领域的研究提供了重要的工具。
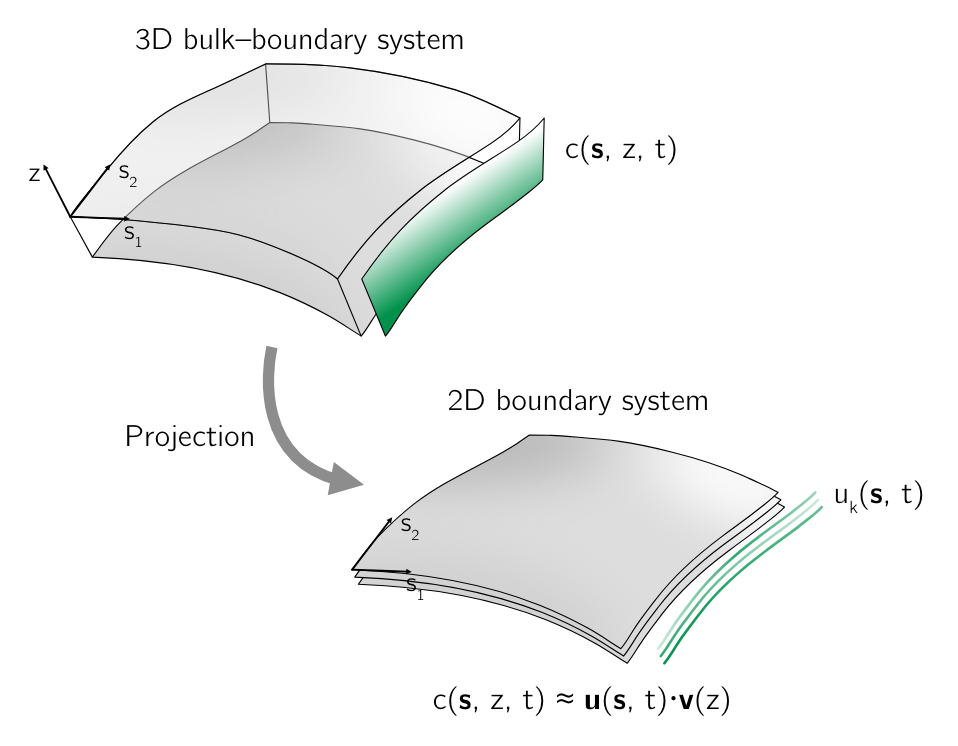
图1. 三维体边界系统中随时间变化的体场 c(s, z, t)(由绿色(灰色)切片表示)通过近似值投影到域的二维边界上的示意图。
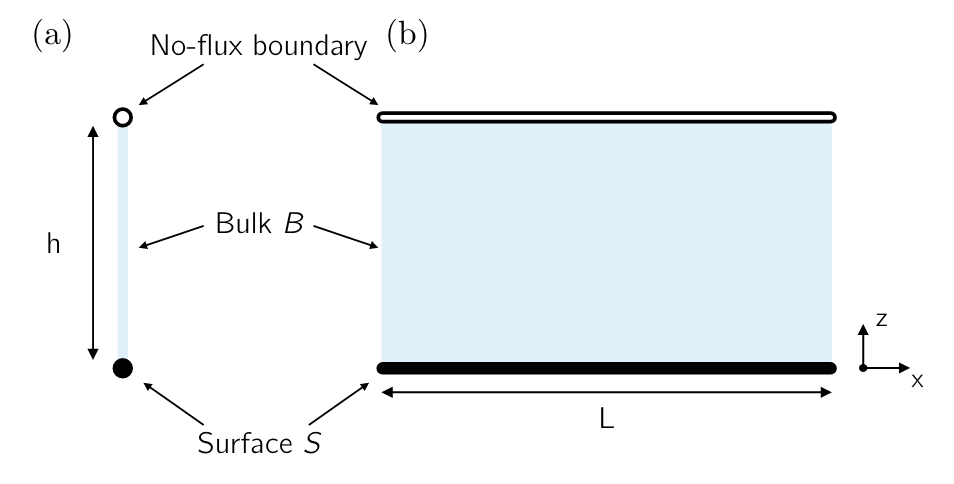
图2. 平面几何图形的可视化示意图。(a) 大小为 h 的一维块域 B(胞质溶胶,蓝色/灰色)一侧由反应表面 S(膜,实心圆)界定,另一侧由无通量边界(空心圆)界定)。(b) 对于高度为 h 和宽度为 L 的二维体域,表面 S 是一维线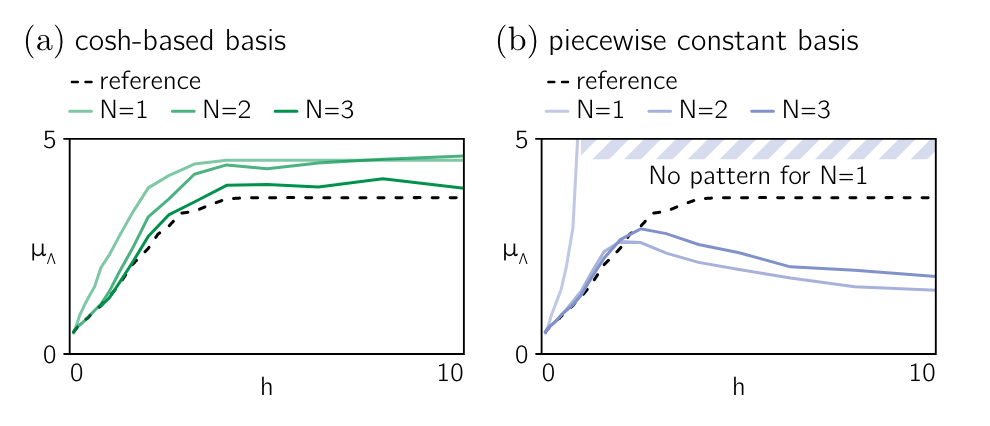
图3. 使用不同基选择的投影方法进行粗化后的平均峰值距离 μΛ 的比较。龚铭康 | 编译
6. 加入集智,一起复杂!