本文深入探讨了线性表示中一维和多维特征的区别。文章指出，一维特征是指特征结构上的属性，而非激活向量的维度。通过颜色表示的例子，阐明了一维特征是标量值，而多维特征则是在连续流形上的点，这些点定义了射线。文章进一步解释了SAE中神经元的激活，即使单个神经元提供一维信号，一组神经元也可以被视为采样连续流形。最后，文章强调了即使存在多维特征，线性探测技术仍然有效，因为探测可以锁定流形内的对应一维射线，线性行为仍然保持。

💡 一维特征：特征的属性而非激活向量的宽度，如颜色表示中的红、绿、蓝方向的标量值，特征组合是线性的。

🌈 多维特征：颜色在连续流形上的点，定义了射线。通过缩放该点，可以改变强度，且特征组合和强度缩放在线性行为中保持。

🧠 SAEs应用：SAE中的神经元通常产生稀疏独立的一维特征，但多个神经元可以协同激活形成多维特征，这些激活向量在空间中形成连续形状。

🔍 探测与解释：即使存在多维特征，线性探测技术仍有效，因为探测可以锁定多维流形中对应的一维射线，线性行为依然有效。

Published on February 1, 2025 9:10 AM GMT

Chris Olah's “What is a Linear Representation? What is a Multidimensional Feature?” (July Circuits Update) prompted a moment of pause for me regarding the term "one-dimensional feature." I initially conflated that phrase with the number of dimensions in the activation space (for example, the 768 dimensions in GPT‑2 Small). However, Olah uses "one-dimensional" to describe a property of the feature's structure - not the width of the activation vector. In this post, I clarify this distinction and explain the difference between one‑dimensional and multidimensional features in the context of SAEs and linear representations.

 

Here I explain the distinction between one‐dimensional and multidimensional features as they relate to SAEs and linear representations. It uses the example of colour representation and then relates the intuition back to neuron activations in SAEs.

One‐Dimensional Features

Consider a simple scenario: representing colour using separate dimensions. One could imagine a network that has three independent directions in its activation space - a "redness" direction, a "greenness" direction, and a "blueness" direction.

In this model, each feature is a scalar value. The presence of a particular property (e.g. redness) is indicated by a number that scales the corresponding direction. Increasing the intensity of redness corresponds to moving further along the red direction. Feature composition is linear: 

$$\text{Activation}=x_{\text{red}}{W}_{\text{red}}+x_{\text{green}}{W}_{\text{green}}+x_{\text{blue}}{W}_{\text{blue}}$$

Here, each $W$ represents a fixed direction and each $x$ is a single scalar value. This is the one‐dimensional case.

Multidimensional Features

An alternative view is to represent colour as a point on a continuous "colour manifold." In this view, a colour is not defined solely by independent red, green, and blue scalars. Instead, it occupies a position in a multidimensional space where similar colours are nearby. For example, a circular disk could represent hues, with each point corresponding to a particular shade.

Any chosen point on this manifold defines a one‐dimensional "ray." Scaling the chosen point (multiplying by a scalar) produces a change in intensity without leaving the ray. In effect, the multidimensional feature supports the same operations as a one‐dimensional feature along any fixed direction through the manifold. The network may represent an infinite collection of one‐dimensional features corresponding to different positions on the manifold.

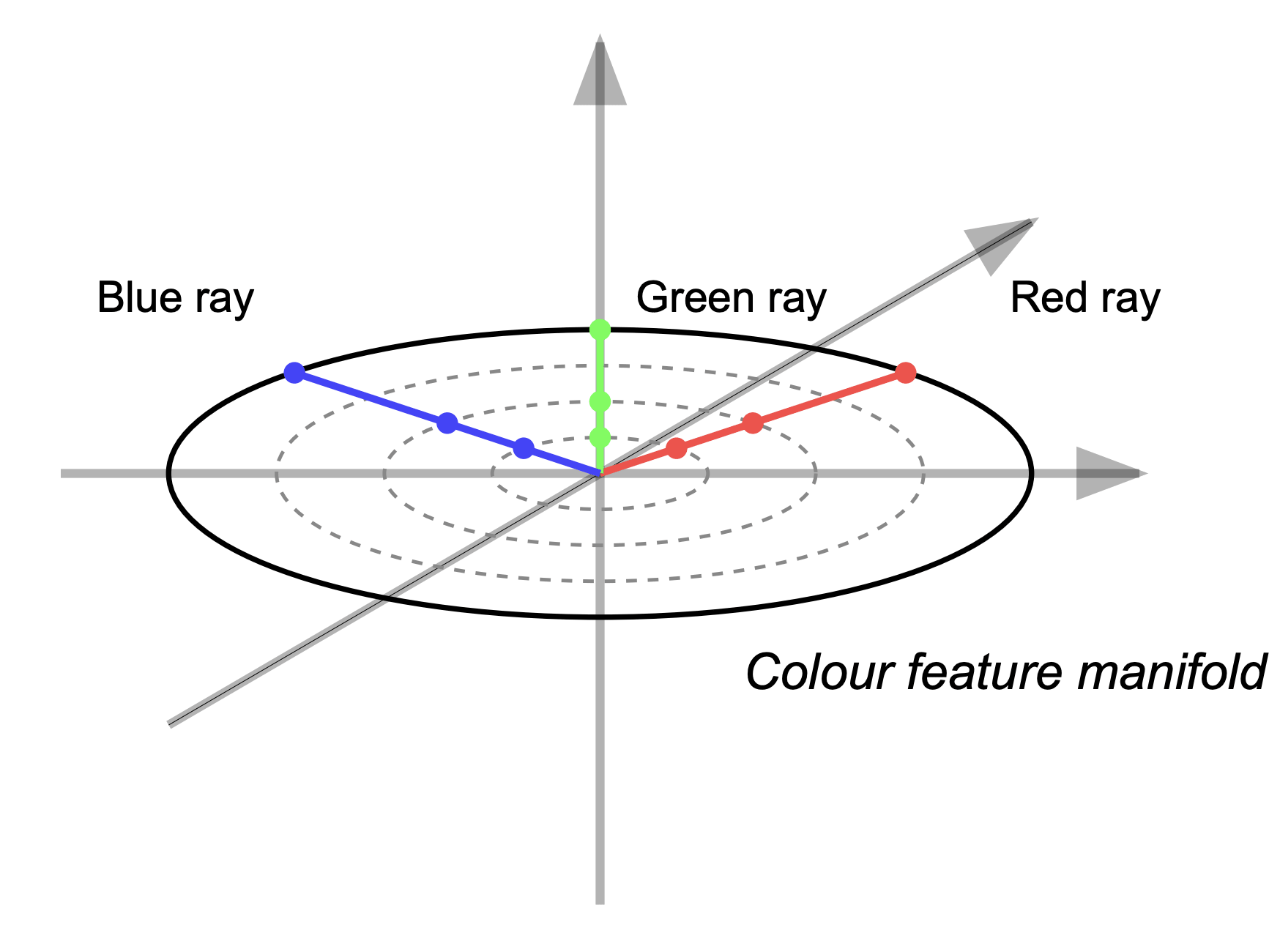
Application to SAEs

SAEs are typically trained to produce sparse, independent features. Each neuron's activation is a scalar, representing a one‐dimensional feature. In practice, however, several neurons may activate together in a structured way. Analysis may reveal that neurons can consistently fire together, potentially indicating a latent, multidimensional feature. When plotted, the activation vectors of such neurons could form a continuous shape in activation space. Furthermore, if scaling the co-activations produces a clear change in intensity while preserving the geometric structure, the behaviour is analogous to scaling along a ray in a multidimensional manifold.

This approach implies that even though individual neurons provide one‐dimensional signals, groups of neurons can be interpreted as sampling a continuous manifold. In that sense, one can think of a multidimensional feature as a collection of one‐dimensional features arranged in a continuous geometric structure.

Implications for Probing and Interpretation

Probing techniques that extract linear directions remain valid even in the presence of multidimensional features. When one is interested in a specific property (for example, a particular shade of orange on a colour disk), a probe can lock onto the corresponding one‐dimensional ray within the overall manifold. The linear behaviour - composition by addition and intensity by scaling - persists on the ray even if the full feature is multidimensional.

---

Hopefully this explanation clarified how one can reconcile the idea of linear representations with the possibility of multidimensional features, particularly given confusion around the actual dimensionality of the activation space being conflated with "one-dimensional feature". 

Discuss