本文探讨了拉普拉斯继承规则在推断二元事件概率时的局限性，认为其基于均匀先验的假设存在问题。作者指出，均匀先验未能体现简单概率过程的本质不对称性，也无法正确赋予确定性程序和简单分数概率以权重。因此，作者提出了一种新的混合先验分布，该分布将对数正态分布、狄拉克函数、托梅分布和均匀分布混合在一起，分别解决概率分布在对数几率上的扩展、确定性程序的权重、简单分数概率的权重以及拉普拉斯原始先验的问题。作者认为，这种混合分布更符合现实世界中未知过程的特性，例如确定性、公平或随机性等。

🤔 **均匀先验的局限性：**均匀先验假设所有概率区间同样可能，但忽略了简单概率过程通常更倾向于产生接近0的概率，且难以构造产生特定概率（例如0.3456）的简单程序。这导致均匀先验无法捕捉简单概率过程空间中的基本不对称性。

🤔 **确定性程序的权重：**均匀先验认为过程几乎不可能是确定性的，即概率为0或1的可能性为零。但实际上，存在非常简单的确定性程序（始终输出0或1），合理的先验分布应该赋予这些简单程序非零的概率。

🤔 **简单分数概率的权重：**均匀先验为像p=1/2或p=5/6这样的简单分数分配了零概率，这也不合理。为了解决这个问题，作者引入了托梅分布，为这些简单分数赋予更高的权重。

🤔 **混合先验分布：**作者提出了一个混合先验分布，包括对数正态分布、狄拉克函数、托梅分布和均匀分布，分别解决概率分布在对数几率上的扩展、确定性程序的权重、简单分数概率的权重以及拉普拉斯原始先验的问题。

🤔 **科尔莫哥洛夫复杂度：**理想情况下，先验分布应该包含所有可能的概率程序，并根据其科尔莫哥洛夫复杂度加权。但由于这种分布难以表示和计算，作者提出了一个可处理的混合先验分布作为替代方案。

Published on November 22, 2024 6:46 PM GMT

Imagine a sequence of binary outcomes generated independently and identically by some stochastic process. After observing N outcomes, with n successes, Laplace's Rule of Succession suggests that our confidence in another success should be (n+1)/(N+2). This corresponds to a uniform prior over [0,1] for the underlying probability. But should we really be uniform about probabilities?

I think a uniform prior is wrong for three reasons:

The uniform prior suggests we should be equally surprised if the underlying probability lies in [0, 0.0001] as in [0.3456, 0.3457]. But this seems wrong. Many simple programs would give probabilities near 0 — for example, any process that succeeds only in rare edge cases. In contrast, it's harder to construct simple programs that give probabilities specifically around 0.3456. The uniform prior fails to capture this fundamental asymmetry in the space of simple probabilistic processes. An appropriate prior distribution would spread probability across a wide range of log-odds.Under the uniform prior, the process is almost surely not deterministic — i.e. the prior likelihood of p being exactly 0 or 1 is zero. This seems wrong. Among probabilistic programs that generate binary outcomes, there are very simple deterministic ones (always output 0 or 1). An appropriate prior should have nonzero prior probability on these simple programs.The uniform prior assigns zero probability to simple fractions like p=1/2 or p=5/6. This too seems wrong - simple rational probabilities should have higher weight. To fix this, we mix in the Thomae distribution, which adds a weight (m·n)^(-α) to each fraction m/(m+n) for every pair 1 ≤ m,n ≤ 100.

I propose this mixture distribution:

w1 lognormal(0, sigma^2) + w2 0.5(dirac(0) + dirac(1)) + w3 thomae_{100}(α) + w4 uniform(0,1)

where:

The first term captures logistic transformations of normal variables (weight w1), resolving the issue that probabilities should be spread across log-oddsThe second term captures deterministic programs (weight w2), allowing for exactly zero and oneThe third term captures rational probabilities with simple fractions (weight w3), giving weight to simple ratiosThe fourth term captures uniform random number comparisons (weight w4), corresponding to Laplace's original prior

Ideally, our prior should be a mixture of every possible probabilistic program, weighted by 2^(-K) where K is its Kolmogorov complexity. This would properly capture our preference for simple mechanisms. However, such a distribution is impossible to represent, compute, or apply. Instead, I propose my prior as a tractable distribution that resolves what I think are the most egregious problems with Laplace's law of succession.

I've built an interactive demo to explore this distribution. The default parameters (w1=0.3, w2=0.1, w3=0.3, w4=0.3, sigma=5, alpha=2) reflect my intuition about the relative frequency of these different types of programs in practice. This gives a more realistic prior for many real-world scenarios where we're trying to infer the behavior of unknown processes that might be deterministic, fair, or genuinely random in various ways.

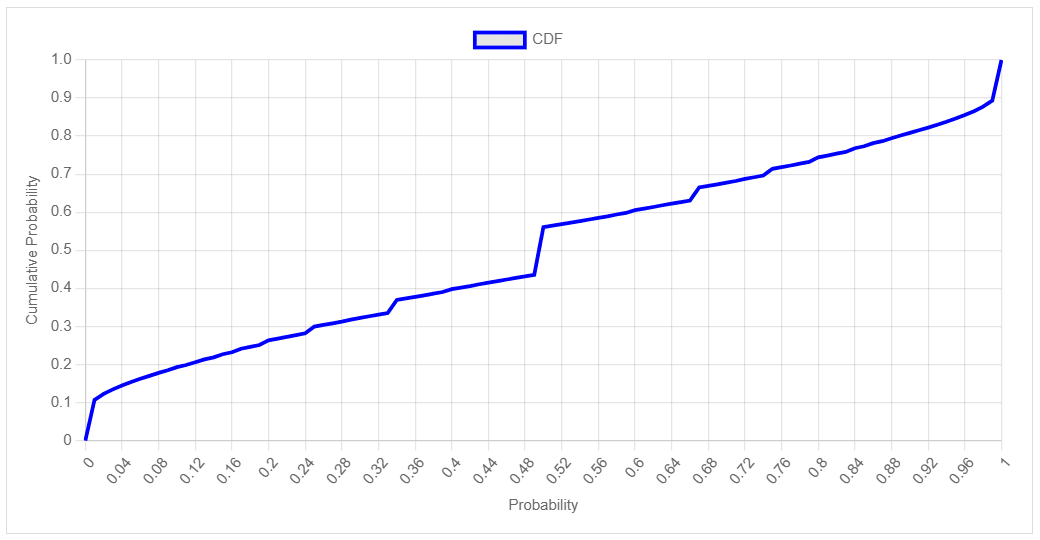
What do you think? Is there a simple model which serves as a better prior?

Discuss