文章探讨了“事后诸葛亮”偏见，即人们在得知一个不确定事件发生后，会高估自己最初的预期。通过对拜登年龄和竞选有效性的讨论，文章指出，在模糊情况下，这种偏见实际上是合理的，因为人们对自己的先验概率不确定，且相信自己的判断与真相相关。

🔍 “事后诸葛亮”偏见是指人们在得知一个不确定事件发生后，会认为自己事先的预期比实际上更高。例如，在拜登年龄的讨论中，人们可能会在第一阶段估计他有60%的可能性太老，而在得知他确实表现不佳后，会回忆起自己当初的估计是70%。

🧠 文章提出，在模糊的情况下，这种偏见是合理的。因为人们对某些事件的先验概率并不确定，比如拜登是否太老而无法有效竞选。这种不确定性使得在得知真相后，人们会调整自己最初的预期。

🤔 文章进一步解释，如果一个贝叶斯观察者在面对不确定的先验概率时，且相信自己的判断与真相正相关，那么他们应该表现出“事后诸葛亮”偏见。这是因为得知真相后，他们对先验概率的估计会上升。

📊 研究表明，当人们面对明确的客观概率时，这种偏见会减少或消失。这表明，在确定性的情况下，人们不会表现出“事后诸葛亮”偏见。

🔍 文章最后指出，虽然“事后诸葛亮”偏见在特定条件下是合理的，但这并不意味着每一个实例都是理性的。在某些情况下，比如当人们对自己的先验判断非常确定时，或者不信任自己的判断时，就不应该表现出这种偏见。

Published on July 20, 2024 1:42 PM GMT

TLDR: You’re unsure about something. Then it happens—and you think to yourself, “I kinda expected that.” Such hindsight bias is commonly derided as irrational. But any Bayesian who (1) is unsure of exactly what they think, and (2) trusts their own judgment should exhibit hindsight bias.

---

Biden is old.

Ever since the disastrous debate, there’s been a flurry of discussion about whether he’s too old to campaign effectively.

Many pundits are saying that they’ve been worried about this for a long time. And—although some of them have—this often looks like hindsight bias.

Hindsight bias—aka the “I knew it all along” effect—is the the finding that when people learn that an uncertain event happened, they increase their estimate for how much they expected it.

In this case, the uncertain claim is Biden is too old to make the case against Trump. Arguably, we’ve learned that it (or something near enough) is true. Given this, it’s natural for pundits to over-emphasize how worried they were, under-emphasize their uncertainty, and end up thinking that they saw this coming.

At the same time, it’s equally natural to look at the pundits, and scoff: “That’s just hindsight bias! They’re trying to make themselves look smarter than they are.”

But that’s wrong. Unless they're fools, they should commit hindsight bias.^[1]

The finding

Hindsight bias is one of those empirical findings that’s both robust, and easy to see in yourself. We should’t worry about replication failures.

There are many variations, but here’s a classic study design:

Stage 1: present people with a series of scenarios, and ask them to predict how likely they think an uncertain outcome is in each case.Stage 2: Distract them for a while, or let them go about their day.Stage 3: Inform them of the true outcome in each scenario, and ask them to recall how likely they originally thought it was.

The typical finding: people exhibit a hindsight shift. On average, their Stage-3 estimates for what their Stage-1 probabilities were are higher than their Stage-1 probabilities.

In our case: at Stage 1, the average person might say they think it’s 60%-likely that Biden is too old. Then, at stage 3, they’ll say that they originally thought it was 70%-likely that he’s too old. That 70 – 60 = 10% gap is the hindsight shift.

For a concrete example, here are the results from Hoffrage et al. 2000—the relevant condition is the “Feedback” condition, with positive values indicating a positive hindsight shift:

 

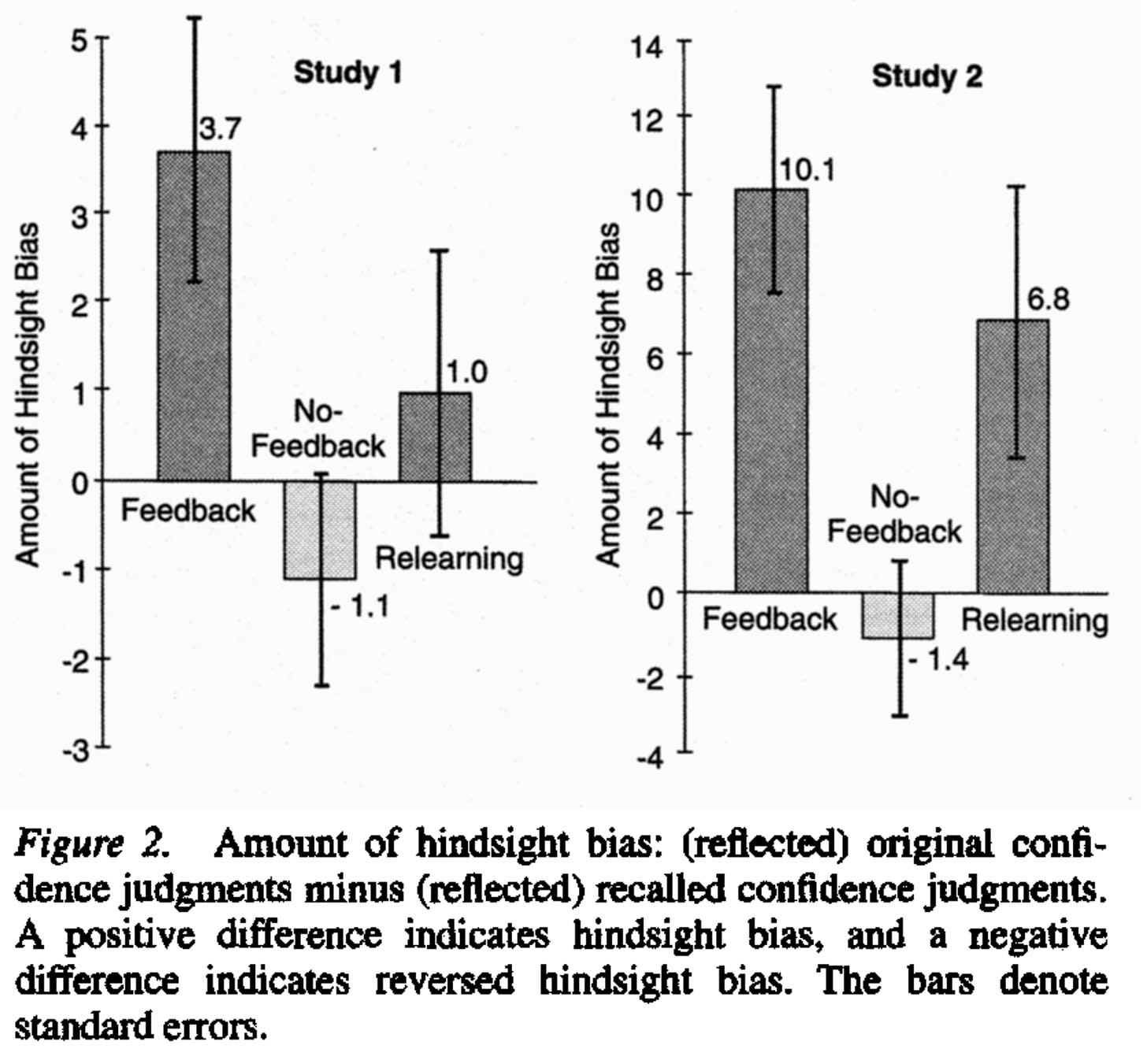
Why it’s rational, intuitively

I say that reasonable people should commit hindsight bias—at least in most real-world and experimentally-studied conditions. Slightly more carefully: under conditions of ambiguity—when its unclear exactly what your prior opinions are—hindsight shifts are rational.

Let’s start with the intuitive argument.

First, notice that when you’re predicting something like whether Biden’s too old to campaign effectively, it makes sense to be unsure of exactly how confident you are.

To see this, contrast it with cases where it’s completely clear how confident you are: you know you’re (exactly) 50%-confident that this fair coin will land heads; you know that you’re (exactly) 25%-confident that the first card drawn from this deck will be a spade, etc.

Predicting (even a suitably sharpened^[2]) version of whether Biden’s too old is not like that. If forced, you’ll name a number—say, 75%. But you’re not completely confident that this number accurately captures your opinion. Maybe, in fact, you really think it’s slightly more likely that Biden’s too old than that a coin won’t land heads twice in a row (in which case you’re more than 75%); maybe you think it’s slightly less likely (in which case you’re less than 75%). You shouldn’t be sure.

Second, consider what happens in the third-person case, when we’re unsure how confident someone else is of something.

Forget Biden—let’s talk about something important.

Do I like broccoli? I’m guessing you’re not sure. Now—I know this’ll be difficult—but what’s your estimate for how likely my brother thinks it is that I like broccoli? Hard to say, but pick a number. Say, 60%.

Now I’ll tell you a secret: I do like broccoli.

Given your new knowledge, what’s your updated estimate for how likely my brother thought it was that I like broccoli? Obviously, your estimate should go up! (Say, to 80% or 90%.) For now you should think: “Well, there was always a good chance Kevin’s brother knew whether he likes broccoli. Now that I know that Kevin does like broccoli, there’s a good chance his brother was confident of that.”

More generally: when you think a quantity, X (e.g. my brother’s subjective probability that I like broccoli) is correlated with the truth-value of a claim e (e.g. that I like broccoli), then learning e should raise your estimate of X.

Here’s the kicker: the same is true when X is your prior probability for e.

As we’ve said: you should be unsure what exactly your prior is that Biden is too old. And so long as you trust your judgment, you should think whatever your true prior is, it’s correlated with the truth.

Upshot: if you learn that Biden is too old to campaign effectively, that should increase your estimate for how likely you thought this was to begin with. You should exhibit a hindsight shift.

Let’s make the argument more precise.

Why it’s rational, precisely

Hindsight bias captures how your estimate of a fixed quantity—the probability you assigned to e at the initial time—changes over time. When people are asked how confident they are, they give one number. When they’re later asked how confident they were, they give a higher number.

In general, for any quantity X, a Bayesian’s estimate for X is their expectation E(X)—a probability-weighted average of X’s various possible values.^[3]

For instance, if your probability distribution over how tall I am is the below bell curve, then the dashed line—the mean of the distribution—is your estimate for my height:

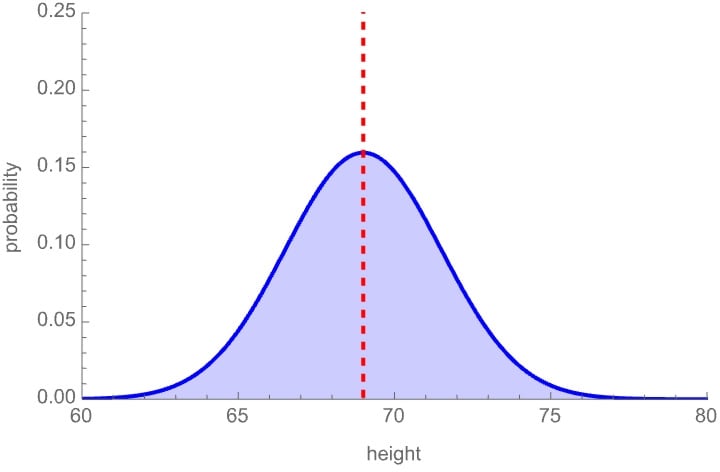
Prior probability distribution and estimate of my height

Your estimate for my height X after learning a proposition e is simply your expectation E(X|e) of X relative to your updated probability function P(•|e).^[4] For instance, if you learn that I wear a shoe size greater than 10, that might shift your distribution over my possible heights—and resulting estimate—like this:

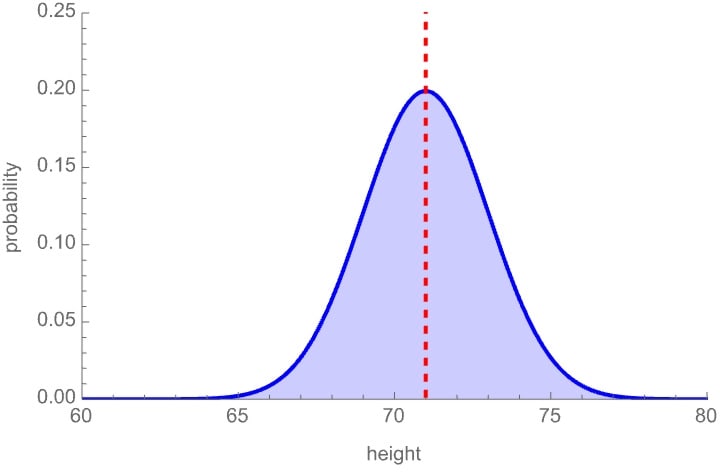
Posterior probability distribution and estimate of my height

So in this case, learning e raises your estimate for my height: E(X|e) > E(X).

Now let’s translate this to hindsight bias.

Let P be your subjective probability distribution when you’re making your initial judgment. Let e be the target claim of interest—say, that Biden is too old to campaign effectively. The quantity of interest is your prior probability for that claim, P(e).

Note that—like my height, X—P(e) is a quantity or random variable. It’s the sort of thing that can vary between possibilities. After all, I am uncertain what your prior probability is that Biden is too old—so to model my uncertainty about your priors, we need to model your priors as a variable. Likewise if you are uncertain about your priors. 

(Some of you are probably champing at the bit, thinking "higher-order probability is either trivial or nonsense". While it's true that many attempts to model higher-order probability either are incoherent or reduce to regular Bayesianism, it turns out that nontrivial higher-order probability does make conceptual and mathematical sense—we just need to use the tools from modal and epistemic logic.  See e.g. this paper,  this introductory paper, or the Appendix below, for mathematical details.)

Your prior estimate for your prior probability is simply E(P(e)).^[5] Your posterior estimate for your prior, after learning e, is E(P(e)|e). You commit hindsight bias if the latter is higher than the former: E(P(e)|e) > E(P(e)).

So, when should you commit hindsight bias? Exactly when the following two assumptions hold:

Prior Uncertainty: Your prior is uncertain what your prior credence in e is.
(Precisely: P(P(e) = a) < 1, for all numbers a.)
Prior Trust: You think your prior (whatever it is) is correlated with the truth.
(Precisely: your prior P(e) and e’s truth-value 1_e have positive covariance, Cov[P(e), 1_e] > 0, relative to your prior probability function P.)^[6]

(In fact, Prior Uncertainty follows from Prior Trust—I’m just making it explicit.)

Who would violate these assumption? Only fools.

The only way to violate Prior Uncertainty is to be completely certain of exactly how likely you think it is that Biden is too old. You’d have to be willing to bet your life that the number you name isn’t off by 0.0001 percentage points. Only fools would be so confident in their ability to articulate their true opinions.

The only way to violate Prior Trust is to think that your true probability is either uncorrelated or negatively correlated with the truth. This is a radical form of distrusting your own judgment. Only (people who have reason to think that they are) fools would do so.

Here’s the kicker: any Bayesian who satisfies Prior Uncertainty and Prior Trust will commit hindsight bias:

Fact: E(P(e)|e) > E(P(e)) if and only if Cov[P(e), 1_e] > 0. (Proof in Appendix.)

Informally: you should commit hindsight bias iff you trust yourself.

In other words: only fools avoid hindsight bias.

What to make of this?

Obviously this doesn’t show that any given instance of hindsight bias is rational.

In fact, it gives us clear conditions under which hindsight bias is not rational: if (1) you are certain of what your prior judgment was—for example, when you have clear evidence about the objective probabilities—or (2) you don’t trust your prior judgment, then you shouldn’t commit hindsight bias.

Indeed, there’s some empirical evidence that having clear objective probabilities—the sort of thing that should make you certain of what your prior was—reduces or eliminates hindsight bias. (See this paper, experiment 5.)

Moreover, nothing here shows that the degree to which people commit hindsight bias is rational—they may well trust their priors too much.

But the mere fact that people commit hindsight bias is not evidence that they are irrational. In fact, if they didn’t commit hindsight bias, that would be clear evidence that they’re irrational!

So let’s follow the pundits: we knew all along that Biden was too old. Probably.

Appendix

Here’s the Technical Appendix—including (1) an example probabilistic model illustrating hindsight bias, and (2) a proof of the Fact.

1. ^{^}

   The argument I’m going to give is inspired by (and a generalization of) Brian Hedden’s 2019 paper, “Hindsight bias is not a bias”.

2. ^{^}

   If you’re worried that “Biden’s too old to campaign effectively” is too vague to have a truth value, then replace it with a precise (but long-winded) alternative, like “Biden’s campaign will fail to recover it’s June 27 position in the polls by August 27”, or some such. The argument goes through either way.

3. ^{^}

   Precisely (assuming for simplicity that X has finite support) with P their probability function and X(w) the value of X at w:

   $$E\left(X\right):=\sum _{a\in R}P(X=a)\cdot a=\sum _{w\in W}P\left(w\right)\cdot X\left(w\right)$$
4. ^{^}

   Again assuming X has finite support:

   $$E\left(X|e\right):=\sum _{x\in R}P(X=a|e)\cdot a=\sum _{w\in W}P\left(w|e\right)\cdot X\left(w\right)$$
5. ^{^}

   As always, this is defined the same way:

   $$E\left(P\right(e\left)\right)=\sum _{a\in R}P\left(P\right(e)=a)\cdot a$$

   This might turn out to equal your prior: E(P(e)) = P(e). But this doesn’t matter for our purposes; and I won’t assume anything about that. (In the context of higher-order uncertainty, that equation will often fail.)

   You might notice that if P is a random variable, then E(P(e)) is too—it can vary from world to world. When we write something like P(e) or E(P(e)) unembedded, they take the values that they take at the actual world @ in the model.

6. ^{^}

   The truth-value of e, 1_e, is e’s indicator variable: it takes value 1 if e is true and 0 if it’s false. The covariance of two variables X and Y is a (non-normalized) measure of their correlation: Cov[X,Y] := E(XY) – E(X)•E(Y). In our case: Cov[P(e), 1_e] = E(P(e)•1_e) – E(P(e))•E(1_e). The familiar correlation coefficient is the normalized covariance.

Discuss