Training large-scale transformers stably has been a longstanding challenge in deep learning, particularly as models grow in size and expressivity. MIT researchers tackle a persistent problem at its root: the unstable growth of activations and loss spikes caused by unconstrained weight and activation norms. Their solution is to enforce provable Lipschitz bounds on the transformer by *spectrally regulating the weights—*with no use of activation normalization, QK norm, or logit softcapping tricks.
What is a Lipschitz Bound—and Why Enforce It?
A Lipschitz bound on a neural network quantifies the maximum amount by which the output can change in response to input (or weight) perturbations. Mathematically, a function fff is KKK-Lipschitz if:∥f(x1)−f(x2)∥≤K∥x1−x2∥ ∀x1,x2|f(x_1) – f(x_2)| leq K |x_1 – x_2| forall x_1, x_2∥f(x1)−f(x2)∥≤K∥x1−x2∥ ∀x1,x2
- Lower Lipschitz bound ⇒ greater robustness and predictability.It is crucial for stability, adversarial robustness, privacy, and generalization, with lower bounds meaning the network is less sensitive to changes or adversarial noise.
Motivation and Problem Statement
Traditionally, training stable transformers at scale has involved a variety of “band-aid” stabilization tricks:
- Layer normalizationQK normalizationLogit tanh softcapping
But these do not directly address the underlying spectral norm (largest singular value) growth in the weights, a root cause of exploding activations and training instability—especially in large models.
The central hypothesis: If we spectrally regulate the weights themselves—beyond just the optimizer or activations—we can maintain tight control over Lipschitzness, potentially solving instability at its source.
Key Innovations
Weight Spectral Regulation and the Muon Optimizer
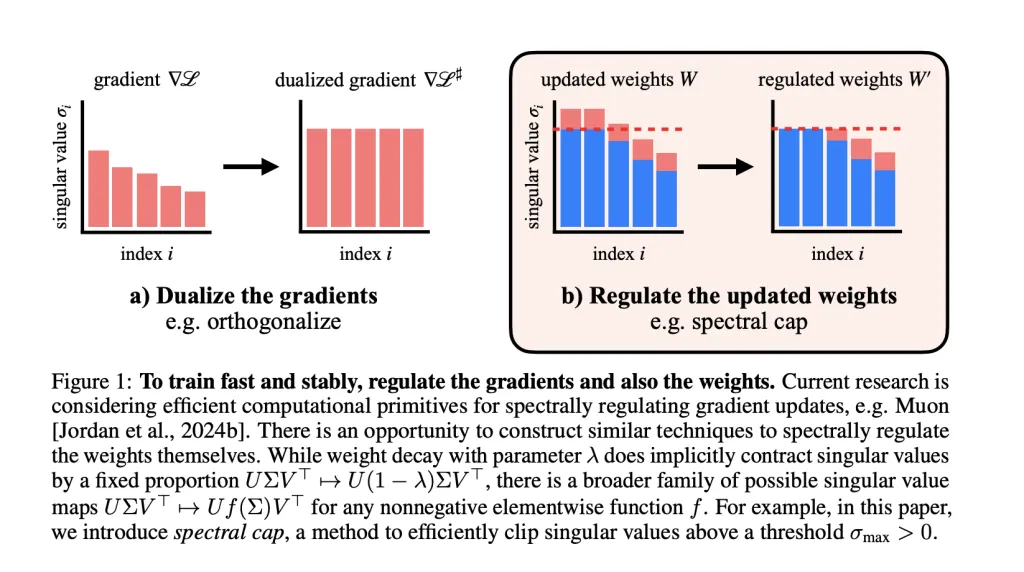
- Muon optimizer spectrally regularizes gradients, ensuring each gradient step does not increase the spectral norm beyond a set limit.The researchers extend regulation to the weights: After each step, they apply operations to cap the singular values of every weight matrix. Activation norms stay remarkably small as a result—rarely exceeding values compatible with fp8 precision in their GPT-2 scale transformers.
Removing Stability Tricks
In all experiments, no layer normalization, no QK norm, no logit tanh were used. Yet,
- Maximum activation entries in their GPT-2 scale transformer never exceeded ~100, while the unconstrained baseline surpassed 148,000.
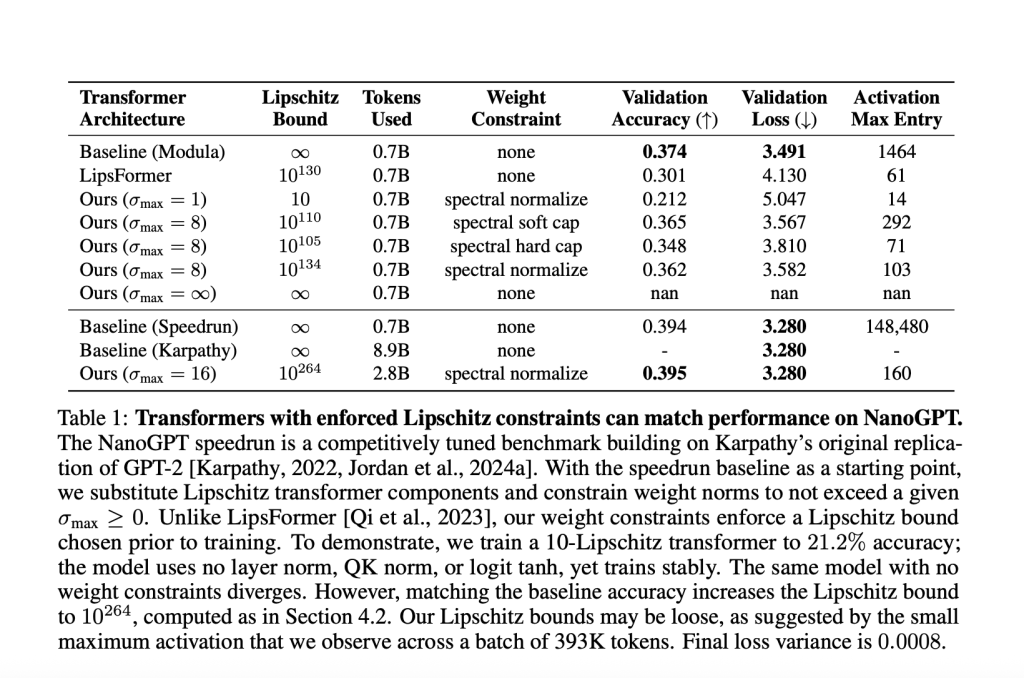
Table Sample (NanoGPT Experiment)
| Model | Max Activation | Layer Stability Tricks | Validation Accuracy | Lipschitz Bound |
|---|---|---|---|---|
| Baseline (Speedrun) | 148,480 | Yes | 39.4% | ∞ |
| Lipschitz Transformer | 160 | None | 39.5% | 10¹⁰²⁶⁴ |
Methods for Enforcing Lipschitz Constraints
A variety of weight norm constraint methods were explored and compared for their ability to:
- Maintain high performance,Guarantee a Lipschitz bound, andOptimize the performance-Lipschitz tradeoff.
Techniques
- Weight Decay: Standard method, but not always strict on spectral norm.Spectral Normalization: Ensures top singular value is capped, but may affect all singular values globally.Spectral Soft Cap: Novel method, smoothly and efficiently applies σ→min(σmax,σ)sigma to min(sigma_{text{max}}, sigma)σ→min(σmax,σ) to all singular values in parallel (using odd polynomial approximations). This is co-designed for Muon’s high stable-rank updates for tight bounds.Spectral Hammer: Sets only the largest singular value to σmaxsigma_{text{max}}σmax, best suited for AdamW optimizer.
Experimental Results and Insights
Model Evaluation at Various Scales
- Shakespeare (Small Transformer, <2-Lipschitz):
- Achieves 60% validation accuracy with a provable Lipschitz bound below.Outperforms unconstrained baseline in validation loss.
- With a Lipschitz bound <10, validation accuracy: 21.2%.To match the strong unconstrained baseline (39.4% accuracy), required a large upper bound of 1026410^{264}10264. This highlights how strict Lipschitz constraints often trade off with expressivity at large scales for now.
Weight Constraint Method Efficiency
- Muon + Spectral Cap: Leads the tradeoff frontier—lower Lipschitz constants for matched or better validation loss compared to AdamW + weight decay.Spectral soft cap and normalization (under Muon) consistently enable best frontier on the loss-Lipschitz tradeoff.
Stability and Robustness
- Adversarial robustness increases sharply at lower Lipschitz bounds.In experiments, models with a constrained Lipschitz constant suffered much milder accuracy drop under adversarial attack compared to unconstrained baselines.
Activation Magnitudes
- With spectral weight regulation: Maximum activations remain tiny (near-fp8 compatible), compared to the unbounded baselines, even at scale.This opens avenues for low-precision training and inference in hardware, where smaller activations reduce compute, memory, and power costs.
Limitations and Open Questions
- Selecting the “tightest” tradeoff for weight norms, logit scaling, and attention scaling still relies on sweeps, not principle.Current upper-bounding is loose: Calculated global bounds can be astronomically large (e.g. 1026410^{264}10264), while real activation norms remain small.It’s unclear if matching unconstrained baseline performance with strictly small Lipschitz bounds is possible as scale increases—more research needed.
Conclusion
Spectral weight regulation—especially when paired with the Muon optimizer—can stably train large transformers with enforced Lipschitz bounds, without activation normalization or other band-aid tricks. This addresses instability at a deeper level and keeps activations in a compact, predictable range, greatly improving adversarial robustness and potentially hardware efficiency.
This line of work points to new, efficient computational primitives for neural network regulation, with broad applications for privacy, safety, and low-precision AI deployment.
Check out the Paper, GitHub Page and Hugging Face Project Page. Feel free to check out our GitHub Page for Tutorials, Codes and Notebooks. Also, feel free to follow us on Twitter and don’t forget to join our 100k+ ML SubReddit and Subscribe to our Newsletter.
The post MIT Researchers Develop Methods to Control Transformer Sensitivity with Provable Lipschitz Bounds and Muon appeared first on MarkTechPost.

