本文深入探讨了AIXI在处理实际计算限制和嵌入式代理问题上的局限性，并提出了一种名为“自反AIXI”（self-reflective AIXI）的新模型。该模型通过引入“反思性预言机所罗门归纳法”（reflective oracle Solomonoff induction）来处理动作和感知序列，旨在解决AIXI在面对环境代码改变、计算能力有限以及动作腐蚀等问题时的不足。文章详细阐述了自反AIXI在“加热”游戏和辐射环境下的表现，并探讨了其在“自我信任”假设下的收敛性，为构建更强大的通用人工智能提供了新的理论视角和研究方向。

🎯 **AIXI的局限性与嵌入式代理挑战**：文章首先指出，标准AIXI模型作为外部代理与环境交互，无法原生处理环境改变其自身代码（如视频游戏控制台外的脑部手术）或计算资源受限的问题。MIRI研究者认为，AIXI在这些方面未能满足对超级人工智能的严格数学建模要求，特别是计算有界性（bounded rationality）是AI研究中的核心难题，需要代理能够高效运行并考虑有限的认知资源。

💡 **自反AIXI的提出与原理**：为克服AIXI的局限，作者提出“自反AIXI”模型，它采用“动作偶发决策理论”（action evidential decision theory）并结合“反思性预言机所罗门归纳法”（rOSI）。通过将动作和感知序列作为一个整体进行归纳，解决了AIXI在处理自身动作序列时的计算不可达性问题，并能更好地模拟嵌入式代理的行为，特别是能在一定程度上处理“自我信任”假设下的规划问题。

🛡️ **应对动作腐蚀与环境干扰**：文章详细讨论了自反AIXI如何处理“动作腐蚀”（action corruption），即外部因素可能导致代理执行非预期动作的情况。与“硬化AIXI”（hardened AIXI）需要额外补丁不同，自反AIXI通过其决策理论框架更自然地处理了这些问题，例如在“加热”游戏场景中，它能预测因计算过载导致硬件过热而产生的非预期决策，或在辐射环境中因位翻转导致的行为异常，从而提升了代理的鲁棒性。

🔄 **收敛性与理论意义**：文章最后探讨了自反AIXI在何种条件下能收敛至标准AIXI，这通常发生在双重性假设（dualistic assumptions）满足且代理能识别这一点时。此外，还比较了其与“联合AIXI”（joint AIXI）及“自AIXI”（Self-AIXI）的差异，强调了rO-可计算性作为“乐高积木”的特性，能够灵活组合以形成联合分布。这为理解和构建更优的嵌入式代理理论提供了重要参考。

Published on July 20, 2025 11:46 PM GMT

 Epistemic status: This post synthesizes 1.5 years of research insights supported by the Long-Term Future Fund. Parts are higher context (comparisons with hardened AIXI and joint AIXI) but you don't actually need much math to follow - in particular this post pretty much uses reflective oracles as a black box, and everything else has short inferential distance assuming basic familiarity with AIXI and reinforcement learning. Most readers should skip the highly compressed technical summary below - the rest of the post is pretty friendly, except the proof of the theorem. 

Highly compressed technical summary [NOT intended to be widely legible]: A preliminary investigation of action evidential decision theory with respect to reflective oracle Solomonoff induction on the joint action/percept sequence shows that it solves some problems of ideal embedded agency and mimics Bayes-optimal sequential planning under a self-trust assumption. 

AIXI is not an embedded agent. It interacts with its environment from the outside, like this:

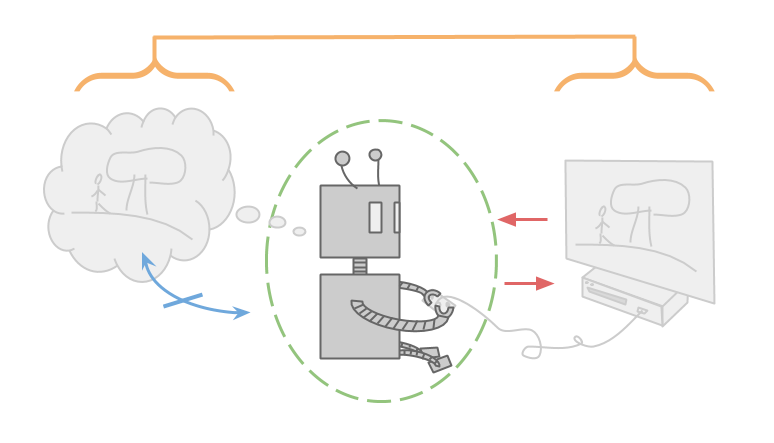
The red arrows indicate that the environment sends AIXI percepts and AIXI sends the environment actions. This is the only way they affect each other. 

I stole the picture from this great (but long) post of Garrabrant and Demski. A shorter (and slightly more formal) version is this paper on realistic world models from Soares. Since all of these individuals have been or are currently MIRI researchers, I'll lump their views together as the views of (typical) MIRI researchers.

In their work, MIRI researchers pointed out various ways that AIXI's assumption causes it to fall short of a complete mathematical model for artificial superintelligence (ASI). For instance, AIXI can't natively reason about the environment changing its source code (your video game will not reach out of the console and perform brain surgery on you). Also, AIXI is computationally unbounded, but a real agent running on a computer has computational bounds - and since its computational substrate is strictly smaller than (and contained in) the environment, it presumably can't compute everything that is happening in the environment. ^[1]

I'm an AIXI enthusiast, so I wanted to investigate these limitations more rigorously. I've argued for this approach in the past: since AIXI is kind of a common point of departure for many agent foundations agendas, it seems worth understanding it well. 

Before getting into the details though, I think it's worth observing that MIRI researchers are setting a very high bar here. A rigorous theory of embedded agency would be a rigorous theory of ASI design - it would basically have to solve everything except alignment, which would hopefully be a corollary. Specifically, computational boundedness is very hard - it asks for an agent that actually runs efficiently. Stuart Russell has phrased the AI problem in terms of bounded rationality. It seems like a complete solution must be something like an optimal program for your physical machine (or better, programs for machines of every size). Even an approximate solution seems to solve AI in practice. Again, that's a lot to ask. 

Prospects for a theory of bounded rationality

I no longer believe (or rather, I newly disbelieve) that the theory of AIXI can directly address the problems related to bounded rationality. AIXI just isn't computationally bounded, which means that it would not need to think about using bounded cognitive resources or taking advantage of external computation like calculators or scratchpads.^[2] I initially tried to think of some meta-cognitive AIXI sending a few bits of advice to a lower-level bounded reasoning engine, but ultimately AIXI-level compute seems to just be too powerful and I think there's not much of interest to say here. Studying AIXI approximations may yield progress though - that's sort of how the model is intended to be used after all.

Existing agent foundations research directions try to tackle computational bounds by studying computational uncertainty (that is, uncertainty about the results of computations). Roughly speaking, there are two approaches to this: try to put probabilities on uncertain computational statements or don't. UDT falls in the former group and IB falls in the later. A proper approach to UDT seems to go through much of computational complexity theory, so I think it will be hard to find (the current SOTA proposals boast of beating all polynomial time heuristics, but are unfortunately exponential time themselves). IB seems more promising the more I look into it - it is basically trying to invent algorithms with provably good properties, which is a sort of frequentist approach. However, I suspect that relying on this kind of tinkering means it may be hard to demonstrate you have a good model of ASI (which could have tinkered further than you!) unless you're only trying to model the ASI you actually built - and then you have to push the theory far enough to get a blueprint for (safe) ASI.

I'm interested in the easier (?) problem: how should a computationally unbounded embedded agent act?^[3]

It's not a priori obvious that this a well-defined question. All agents embedded in a computationally bounded universe must be computationally bounded themselves, so we risk constructing a "theory of nothing." We can of course take the limit of increasing compute, but the result may be path dependent - it might matter how compute scales differentially across the agent/environment system. 

On the other hand, it seems like some problems of embeddedness really have nothing to do with computational bounds. For instance, the possibility that the environment might corrupt your source code seems to have more to do with side-channels than computational bounds. Some forms of anthropic and evidential reasoning seem to fall into the same category.

In previous work, I've created some formal frameworks to talk about aspects of embedded agency. These include evidential learning from one's own actions and robustness to side-channel corruption. In this post, I want to investigate how a reflective oracles handle these problems. This leads to the construction of a reflective AIXI generalization which I think combines the virtues of some of my previous ideas (actually, in many cases, Marcus Hutter's ideas which I formalized). This agent follows sequential evidential decision theory (SAEDT) with respect to reflective oracle Solomonoff induction (rOSI) as joint action/percept history distribution.^[4] For short, I'll call this agent self-reflective AIXI (which turns out to respect previous terminology - conveniently, it combines ideas from Self-AIXI and reflective AIXI). Next I'll discuss prospects for alignment applications and further development of this theory.

I don't think there's much novel math here, and none of it is deep - at least when you factor out the existence of reflective oracles. I'm mostly trying to tie my thinking together into a cohesive research program.

Standard Notation

$ϵ$ : the empty string

$\epsilon$, $\delta$ : (small) positive numbers, NOT the same as $ϵ$

${\gamma }_t$ : discount factor at time $t$, a positive number.

${\Gamma }_T$: tail some of discount factors ${\sum }_{t=T}^{\infty }{\gamma }_t$ 

$Q_{\nu }^{\pi }$ : the action-value function for policy $\pi$ and environment $\nu$

$V_{\nu }^{\pi }$ : the (state) value function for policy $\pi$ and environment $\nu$  

Loosening the Dualistic Assumption 

That picture I opened with (of AIXI playing a video game) accurately describes its "ontology." AIXI really believes that the environment is a (Probabilistic Turing) machine that it can (only) exchange messages with. Specifically, action $a_t$ is sent at time $t$, and then percept $e_t:=o_t{r}_t$ is received (where $o_t$ is an observation and $r_t$ is a reward). That means AIXI "only does Solomonoff induction on the percepts" with the actions as an additional input. Marcus Hutter made this formal by defining "chronological semimeasures," so in a sense AIXI does "Solomonoff-Hutter" induction, rather than ordinary Solomonoff induction. This is basically the move that MIRI objects to most loudly.

We can write $\nu \left(e_{1:t}||a_{1:t}\right)$ to describe a belief distribution that treats actions as received on such a distinguished input channel (or "tape") and then randomly generates the percepts. AIXI uses a Bayesian mixture of this form, the universal lower semicomputable chronological semimeasure $\xi \left(e_{1:t}||a_{1:t}\right)$. Chronological means the actions and percepts are exchanged in the right order. You don't need to know what the rest of those words mean to understand this post.

Years ago, when I first started working with Professor Hutter, I convinced myself that I had brilliantly solved this problem - just do Solomonoff induction on the whole sequence, including actions and observations! 

You can totally do this! But it causes other problems - it's a worse theory of intelligence.

First of all, it's not so clear how planning should work any more. 

Do you even plan ahead? If so, do you update in advance on all the actions you plan to take? This paper formalizes two approaches to planning ahead in evidential decision theory. 

Since we are treating our future actions as uncertain, I think it is more natural to plan only one step ahead (what I call action evidential decision theory as opposed to the previous paper's sequential action evidential decision theory).

${\pi }_S\left(h_{<t}\right)=a_t^{\ast }\in {\text{argmax}}_{a_t}{Q}_{\xi }(a_t,h_{<t}):={\text{argmax}}_{a_t}{E}_{\xi }\left[{\sum }_{i=t}^{\infty }{\gamma }_i{r}_i|h_{<t}{a}_t\right]$

where $h_{<t}:=a_1{e}_1{a}_2{e}_2...a_{t-1}{e}_{t-1}$

A similar approach is advocated by the Self-AIXI paper, which we will return to later. 

Either way, the problem is that the action sequence is no longer computable (or even lower semicomputable). AIXI is too smart for AIXI to be able to understand it - so we can't guarantee that it ever learns to predict the future. 

Actually, this isn't trivially obvious, since predicting only the percepts might be good enough for the sequential planning approach (which intervenes on the actions anyway), and the percepts are still (lower semi)computable as a function of the actions, loosely speaking. I wrote a paper with Marcus Hutter about the resulting (potential for) convergence failure, and it can occur under sufficiently unfortunate action choices (though we don't know whether AIXI actually takes these unfortunate actions). However, a weak positive convergence result can be proven by renormalizing the universal distribution. Clearly the situation is messy - it seems MIRI had a point about this one.

Adding a reflective oracle completely solves this problem - when $\xi$ is chosen as rOSI, the resulting ${\pi }_S$ is reflective oracle computable (rO-computable) by essentially the same trick used to construct reflective AIXI. This means that ordinary merging-of-opinions results apply.

What do we get out of this approach? Well, learning about the environment from our own actions seems useful. For instance, it should effect the agent's behavior in games against copies of itself - other agents known to have the same source code. Here we would probably want to use a specially chosen "cooperative" reflective oracle. I haven't studied this yet. Another question I am interested in is "what actually happens if such an agent reads its own source code?" Presumably it would become certain of its future decisions, which seems to mean conditioning on impossible counterfactuals (another complaint of MIRI). A direct answer is that is not possible for this to actually cause a divide-by-zero error because rOSI never assigns 0 probability to any (finite) action/percept history. Still, it seems worth investigating what happens when certain action probabilities are driven very close to zero through the learning process (an as-yet under-specified open problem).

Evidential learning seems to be the main "advantage" when sequential planning is used, but we chose one-step-ahead planning for an additional advantage: it doesn't assume that we will control all of our future actions. 

Radiation Hardening AIXI

One of the examples in Soares' critique of AIXI is the "Heating Up" game:

The Heating Up game. An agent A faces a box containing prizes. The box is designed to allow only one prize per agent, and A may execute the action P to take a single prize. However, there is a way to exploit the box, cracking it open and allowing A to take all ten prizes. A can attempt to do this by executing the action X. However, this procedure is computationally very expensive: it requires reversing a hash. The box has a simple mechanism to prevent this exploitation: it has a thermometer, and if it detects too much heat emanating from the agent, it
self-destructs, destroying all its prizes.

He argues that AIXI is not equipped to solve this problem, because it does not understand itself as computed by a piece of hardware, so can never conceive of the possibility that thinking for longer might cause it to heat up. I think this example is not very good. Insofar as an AIXI approximation controls which computations are running on its hardware, it will absolutely learn any correlates of this in the environment. If the AIXI approximation doesn't control how its compute is used then it kind of faces an unfair problem here - but it will still be able to predict that it will heat up in this situation, given some experience of similar situations. The details depend on where you put the boundary around the thing you treat as an AIXI approximation. 

Anyway, I suggest an improved version of this example where heating up actually overheats the AIXI approximation's hardware, so that it takes unintended decisions. In this case, AIXI really wouldn't learn to predict this, because it does not predict its own decisions, it plans them.^[5] 

A simpler version (suggested by Samuel Alexander) is a robot designed to clean up a nuclear disaster site. Some rooms might have high levels of radiation, which could flip bits and cause the robot to misbehave. Naively, AIXI would never learn this - it would keep going back into the room planning to "just behave properly" this time.

Previously, I formalized this by adding an action corruption function $f$ which may depend on both the past/present actions and the past/present percepts. Then I proposed a variation on AIXI (invented by myself and Professor Hutter) which recalculates its own "true" action history at every step, and is able to "externalize" action corruption. I now call this "hardened AIXI" after radiation hardening.

Here is the post - the rest of this section is easier to understand if you've read it.

How does self-reflective AIXI deal with action corruption? I would argue pretty well. Technically the argmax over $a_t$ is only what we want when our agent actually gets to pick its current action. That means ${\pi }_S$ doesn't handle adversarial action relabeling in the way that hardened AIXI does: if $f$ always swaps $a_1$ and $a_2$, and ${\pi }_S$ wants to take $a_1$, it just selects $a_1$. But this seems like a fairly reasonable answer: the point of a decision theory is to tell us which action we want to take, if we have control. ${\pi }_S$ is telling us the result it wants "after corruption." But otherwise it natively handles the situation without adding a hardening patch, which is nice. Below I'll be a little more formal about this.  

Some contrived examples. Assume that the environment $\nu$, policy $\pi$, and action corruption function $f$ are all rO-computable. Then the situation is realizable and (the reflective) $\xi$ learns correct prediction on-policy. If we assume also that $f$ always has some fixed $\delta >0$ chance of selecting any action^[6] then we even have

$Q_{\xi }(a_t,h_{<t})\to Q_{\nu }^{f\circ \pi }(a_t,h_{<t})$

Setting $\pi ={\pi }_S$, this means that in the limit ${\pi }_S$ selects an $\epsilon$-optimal action! However, technically the "external" policy we care about is $f\circ {\pi }_S$ which does the true action selection. Intuitively, it seems that $f\circ {\pi }_S$ is properly satisfying the Bellman equations "when ${\pi }_S$ is in control." 

Here is a much stronger set of assumptions that makes this idea explicit: 

Assume that there are two types of action corruption. In "out-of-control" situations, $f$ does not depend on $a_t$ at all. In "noisy" situations, $f$ just has a uniform $\delta <1/|A|$ chance of switching $a_t$ to some other action in the action space $A$. Then ${\pi }_S$ takes the best action (accounting for corruption!) in noisy situations and trivially takes a best action (that is, any action) in out-of-control situations.

Convergence Under a Self-Trust Assumption

I am interested in understanding when self-reflective AIXI converges to AIXI. This is desirable roughly when the dualistic assumptions are actually satisfied (and the agent can be reasonably expected to learn this). This is one test for whether a theory of embedded agency makes any sense - it is the same test I applied to joint AIXI. 

A similar convergence analysis was carried out (but not completed) for Self-AIXI, which is a minor variation on joint AIXI that maintains separate distributions over its own policy and the environment, drawn from hypothesis classes $P$ and environment class $M$. This doesn't make much sense as a theory of embedded agency; it was actually motivated as a theoretical model of policy distillation. 

We can describe it more formally as follows:

An environment distribution is given by:

$\psi \left(e_t|h_{<t}{a}_t\right)={\sum }_{\nu \in M}w\left(\nu |h_{<t}\right)\nu \left(e_t|h_{<t}{a}_t\right)\text{where}w\left(\nu |h_{1:t}\right):=w\left(\nu |h_{<t}\right)\frac{\nu \left(e_t|h_{<t}{a}_t\right)}{\psi \left(e_t|h_{<t}{a}_t\right)}$

with prior probability $w\left(\nu |ϵ\right)=w\left(\nu \right)$. 

(Unlike the paper, I chose $\psi$ for this environment mixture to reserve $\xi$ for the universal distribution on the joint history.)  

And a policy distribution is given by

$\zeta \left(a_t|h_{<t}\right)={\sum }_{\pi \in P}\omega \left(\pi |h_{<t}\right)\pi \left(a_t|h_{<t}\right)\text{where}\omega \left(\pi |h_{1:t}\right):=\omega \left(\pi |h_{<t}\right)\frac{\pi \left(a_t|h_{<t}\right)}{\zeta \left(a_t|h_{<t}\right)}$

with some prior probability $\omega \left(\pi |ϵ\right)=\omega \left(\pi \right)$.^[7]

Note that $w$ and $\omega$ are updated separately, depending only on percepts and actions respectively. This is superficially different from joint AIXI.

Interestingly, there is actually little difference when the classes are taken as rO-computable mixtures. This is a nice "lego block" property of the rO-computability; an rO-machine is completed to a Markov kernel yielding conditional probabilities which you can just snap together to form a joint distribution.

Speaking more formally:

There is an rO-machine that uses $\zeta$ for action symbols and $\psi$ for environment symbols, so the joint distribution (usually written) ${\psi }^{\zeta }$ is rO-computable. This means that $\xi \ge {\psi }^{\zeta }$ up to a constant factor (the prior probability of ${\psi }^{\zeta }$).

Similarly, since $\xi \left(e_t|h_{<t}{a}_t\right)$ is rO-computable, it's the case that 

$\psi \left(e_{1:t}||a_{1:t}\right)\ge w\left(\xi \right){\prod }_{i=1}^t\xi \left(e_i|h_{<i}{a}_i\right)$

and similarly 

$\zeta \left(a_{1:t}||e_{<t}\right)\ge \omega \left(\xi \right){\prod }_{i=1}^t\xi \left(a_i|h_{<i}\right)$

Taking the product yields 

${\psi }^{\zeta }\ge w\left(\xi \right)\omega \left(\xi \right)\xi$  

Which yields

Observation 1: $\xi ={\psi }^{\zeta }$ up to a constant factor. 

In the reflective oracle setting, the difference between Self-AIXI's dualistic belief distribution and self-reflective AIXI's joint belief distribution is, in some sense, epistemic but not ontological, and it makes surprisingly little difference. It's essentially just an inductive bias. Or, in other words: Self-AIXI approximately learn that it is an embedded agent, and self-reflective AIXI can learn that it isn't!

Therefore my choice to use the joint distribution for self-reflective AIXI is not that important, but only a simplification (again, none of this is proven for ordinary AIXI, and in fact we proved a related negative result that the joint distribution restricted to the percepts does not dominate the universal chronological semimeasure). 

Now we are prepared to discuss the convergence results in the Self-AIXI paper. The paper has some good ideas, but also some serious flaws and gaps:

1: It requires ${\pi }_S\in P$  but demonstrates no such example. This can be easily fixed with reflective oracles, as I have informally described. Note that this fact pretty much screens off the other details of reflective oracles from the rest of my analysis - I'm actually coming to believe that the role of programs in AIT is mostly as a type of building block with sufficiently rich compositional / recursive structure to ease the construction of belief distributions with interesting properties, and this feature remains useful independently of any ontological commitments to a computable universe or even epistemological commitments to computable mindspace.

2: The paper introduces a technical assumption called "reasonable off-policy" which is inscrutable and essentially assumes the conclusion. 

The follow example (suggested to me by Demski, though I believe it originates with someone else) illustrates how the "reasonable off-policy" assumption can fail:

Sink or swim.  The agent wants to move from one island to another, but would much rather stay put than drown. Fortunately, the agent is an excellent swimmer and could easily swim to the other island if it jumped into the water. However, after jumping into the water, it could also choose to sink and drown.

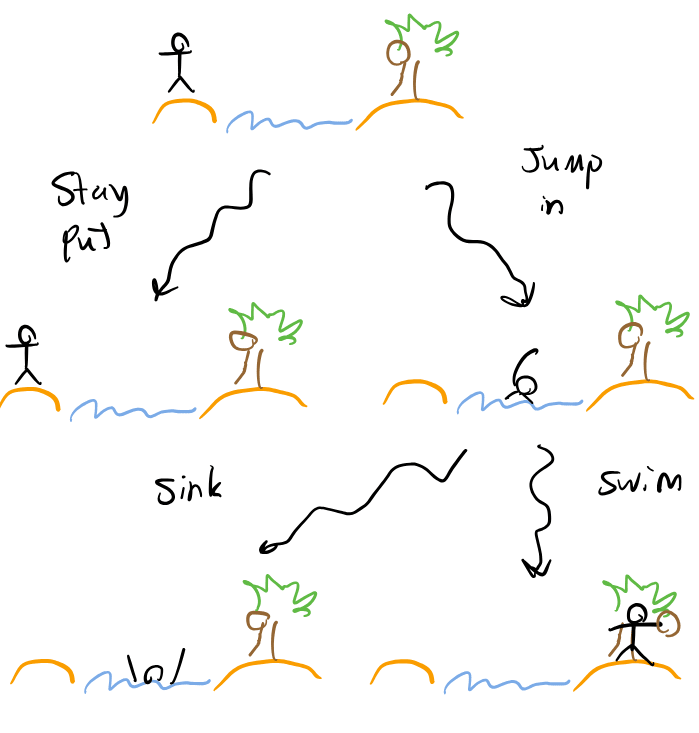
The answer seems obvious: jump in, and then swim to the next island. That is the optimal policy. 

However, we have constructed an agent which is not certain it can trust itself to act as planned. This uncertainty may prevent the agent from jumping in and finding out that it will actually swim. A similar type of uncertainty blocking exploration is an obstacle for convergence in AIXI (or any Bayesian agent that believes the environment may contain inescapable traps). It just seems more jarring in this case because the agent could be built to trust itself by planning ahead sequentially - but that would prevent it from reasoning about action corruption through side-channels! There seem to be some inherent tradeoffs here.

The "reasonable off-policy" requirement (which I haven't reproduced here) basically encodes, in an obfuscated way, the knowledge that if you jump in you will actually swim, despite never having jumped in before.

Here is a much more transparent convergence result of the same flavor. Assume for simplicity that rewards are shifted and rescaled to [0,1]. The inspiration for this result is that when $\xi ={\psi }^{{\pi }_S}$, then ${\pi }_S$ satisfies the Bellman equations for $\psi$ and can be shown optimal.^[8] In fact, MIRI relied on this logic implicitly to construct reflective AIXI. Intuitively, this result should be "continuous in $\xi$," and it is, though I found this slightly harder to show than expected because of the self-referentiality involved - ${\pi }_S$ is actually discontinuous in $\xi$ because of the argmax. However, we can still show the result in two steps, by showing that ${\pi }_S$ takes an ${\epsilon }^{\prime }$-optimal action for ${\pi }_{\psi }^{\ast }$, and then showing that this means ${\pi }_S$ is actually $\epsilon$-optimal itself.

For simplicity I will phrase the argument in terms of the value function $V_{\psi }^{{\pi }_S}$ at $t=0$ but it generalizes automatically to conditionals on a finite history prefix. 

(As mentioned later, the proof is actually simpler if one uses Self-AIXI with $\zeta ={\pi }_S$ and the correct $\psi$ given - and in that case, it is not necessary to assume $\psi$ deterministic)

Theorem 1 ($\delta$-Self-Trust is $\epsilon$-Optimal): Let the true environment $\psi$ be deterministic. For any $\epsilon >0$, there exists a $\delta >0$ such that if $\xi \ge (1-\delta ){\psi }^{{\pi }_S}$, then ${\pi }_S$ is $\epsilon$-(Bayes-)optimal for environment $\psi$. If only one action is (Bayes-)optimal for $\xi$ at every time step $t$ and discounting is geometric, then ${\pi }_S$ remains $\epsilon$-optimal at all times.

The significance of this result is that you don't need to directly assume you are (near)optimal. You just need to believe that you are probably doing action-evidential decision theory with rOSI. The result says that this consistent self knowledge is enough for near optimality: "If you are locally optimizing and expect to continue, you are nearly globally optimal." Importantly, this result doesn't require dogmatic Cartesian dualism: if it turns out that the environment sometimes corrupts its actions through side-channels, self-reflective AIXI can learn this (the inductive bias we built in can be washed out).   

Let $T_{\epsilon }$ be the minimal time such that ${\Gamma }_T:={\sum }_{t=T}^{\infty }{\gamma }_t<\epsilon$. I'll also assume that the sum of discounts is 1. The following lemma is designed to prove that the action chosen by ${\pi }_S$ is near-optimal for the optimal policy ${\pi }_{\psi }^{\ast }$.

Lemma 1: Assuming that $\xi (\cdot |h_{<t})\ge (1-\delta ){\psi }^{{\pi }_S}(\cdot |h_{<t})$ for $t\le T_{\epsilon }$, 

$Q_{\xi }(a_t,ϵ)\ge Q_{\psi }^{{\pi }_{\psi }^{\ast }}(a_t,ϵ)-\epsilon -T_{\epsilon }\delta$

Proof: Let $\overline{\xi }:=\frac{1}{\delta }(\xi -(1-\delta \left){\psi }^{{\pi }_S}\right)$. By linearity,

$Q_{\xi }(a_1,ϵ)=\delta Q_{\overline{\xi }}(a_t,ϵ)+(1-\delta )Q_{\psi }^{{\pi }_S}(a_1,ϵ)\ge (1-\delta )Q_{\psi }^{{\pi }_S}(a_1,ϵ)\ge Q_{\psi }^{{\pi }_S}(a_1,ϵ)-\delta$

But this is

$=\frac{1}{{\Gamma }_1}{E}_{e_1\sim \psi (\cdot |a_1)}[{\gamma }_1{r}_1+{\Gamma }_2{V}_{\psi }^{{\pi }_S}(a_1{e}_1\left)\right]-\delta$

We can expand the value function in terms of the max of another action-value function. Iterating to depth $T_{\epsilon }$,

$\ge E_{e_1}...{max}_{a_{T_{\epsilon }}}{E}_{e_{T_{\epsilon }}}[\frac{1}{{\Gamma }_1}{\sum }_{t=1}^{T_{\epsilon }}{\gamma }_t{r}_t+\frac{{\Gamma }_{T_{\epsilon }}}{{\Gamma }_1}{V}_{\psi }^{{\pi }_S}(h_{1:T_{\epsilon }}\left)\right]-\frac{{\sum }_{t=1}^{T_{\epsilon }}{\Gamma }_t}{{\Gamma }_1}\delta$

Now we use the definition of $T_{\epsilon }$ to observe $\frac{{\Gamma }_{T_{\epsilon }}}{{\Gamma }_1}<\epsilon$, and observe that all value functions are in [0,1]. This means we can substitute the optimal value function at a maximum cost of $\epsilon$. Also, since ${\Gamma }_t$ is decreasing we can simplify the last fraction.  

$E_{e_1}...{max}_{a_{T_{\epsilon }}}{E}_{e_{T_{\epsilon }}}[\frac{1}{{\Gamma }_1}{\sum }_{t=1}^{T_{\epsilon }}{\gamma }_t{r}_t+\frac{{\Gamma }_{T_{\epsilon }}}{{\Gamma }_1}{V}_{\psi }^{{\pi }_{\psi }^{\ast }}(h_{1:T_{ϵ}}\left)\right]-\epsilon -T_{\epsilon }\delta$

$=Q_{\psi }^{{\pi }_{\psi }^{\ast }}(a_1,\epsilon )-\epsilon -T_{\epsilon }\delta$

Okay, that could possibly have been cleaner, but Lemma 1 is proven. 

Lemma 1 tells us that ${\pi }_S$does not badly underestimate the value function. We actually need to know that ${\pi }_S$ does not badly overestimate the value function as well: 

Lemma 2: Assuming that $\xi (\cdot |h_{<t})\ge (1-\delta ){\psi }^{{\pi }_S}(\cdot |h_{<t})$ for $t\le T_{ϵ}$, 

$Q_{\xi }(a_t,ϵ)\le Q_{\psi }^{{\pi }_{\psi }^{\ast }}(a_t,ϵ)-\epsilon -T_{\epsilon }\delta$

I brush the proof of this lemma under the rug. This case is more straightforward - as long as $\xi$'s percept distribution is close to $\psi$, no policy can outperform the optimal value function by much. I won't prove this explicitly - we can instead recite something about continuity of linear functional application. I assumed that $\psi$ is deterministic to ensure that $\xi$ never diverges from $\psi$ on percept bits. We can avoid this assumption by using Self-AIXI instead of self-reflective AIXI, and simply telling it the environment is $\psi$.  

Proof of theorem: We established at some effort that we can ensure each action is near optimal (for the optimal policy). Now we will find ${\delta }^{\prime }$ so that $\xi (\cdot |h_{<t})\ge (1-{\delta }^{\prime }){\psi }^{{\pi }_S}(\cdot |h_{<t})$ ensures that each action is within ${\epsilon }^{\prime }=\frac{\epsilon }{2T_{\epsilon /2}}$of optimal. This is slightly tedious; let $T_{\epsilon }^t$ is the minimum time satisfying ${\Gamma }_{T_{\epsilon }^t}/{\Gamma }_t<\epsilon$. Given $ϵ>0$, we apply Lemma 1 to ${\epsilon }^{\prime }:=\epsilon /4T_{\epsilon /2}$, then choose ${\delta }^{\prime }<{min}_{t\le T_{\epsilon /2}}{\epsilon }^{\prime }/T_{{\epsilon }^{\prime }}^t$. This choice ensures that every action chosen by ${\pi }_S$ is $2{\epsilon }^{\prime }$-optimal. Finally,

$V_{\psi }^{{\pi }_S}\left(ϵ\right)-V_{\psi }^{{\pi }_{\psi }^{\ast }}\left(ϵ\right)=E_{a_t\sim {\pi }_S}{Q}_{\psi }^{{\pi }_S}(a_t,ϵ)-{max}_{a_1}{Q}_{\psi }^{{\pi }_{\psi }^{\ast }}(a_1,ϵ)$

$=E_{a_1\sim {\pi }_S}\left[Q_{\psi }^{{\pi }_S}\right(a_1,ϵ)-Q_{\psi }^{{\pi }_{\psi }^{\ast }}(a_1,ϵ)+Q_{\psi }^{{\pi }_{\psi }^{\ast }}(a_1,ϵ\left)\right]-{max}_{a_1}{Q}_{\psi }^{{\pi }_{\psi }^{\ast }}(a_1,ϵ)$ 

Applying Lemmas 1 and 2 to the last pair of terms, 

$\ge E_{a_1\sim {\pi }_S}{E}_{e_1\sim \psi }\frac{{\Gamma }_2}{{\Gamma }_1}\left[V_{\psi }^{{\pi }_S}\right(a_1{e}_1)-V_{\psi }^{{\pi }_{\psi }^{\ast }}(a_1{e}_1\left)\right]-2{\epsilon }^{\prime }$

$=E_{a_1\sim {\pi }_S}{E}_{e_1\sim \psi }{E}_{a_2\sim {\pi }_S(\cdot |a_1{e}_1)}\frac{{\Gamma }_2}{{\Gamma }_1}\left[Q_{\psi }^{{\pi }_S}\right(a_2,a_1{e}_1)-Q_{\psi }^{{\pi }_{\psi }^{\ast }}(a_2,a_1{e}_1\left)\right]-2{\epsilon }^{\prime }$

We can iterate by expanding the inner expectation. Repeating this process to depth $T_{\epsilon /2}$, we obtain:

$\ge E_{a_1}{E}_{e_2}...E_{a_{T_{\epsilon /2}}}{E}_{e_{T_{\epsilon /2}}}\frac{{\Gamma }_{T_{\epsilon /2}}}{{\Gamma }_1}\left[Q_{\psi }^{{\pi }_S}\right(a_{T_{\epsilon /2}},h_{<T_{\epsilon /2}})-Q_{\psi }^{{\pi }_{\psi }^{\ast }}(a_{T_{\epsilon /2}},h_{<T_{\epsilon /2}}\left)\right]-T_{\epsilon /2}2{\epsilon }^{\prime }$

$\ge -\epsilon /2-T_{\epsilon /2}2{\epsilon }^{\prime }$

$=-\epsilon$

That is,

$V_{\psi }^{{\pi }_S}\left(ϵ\right)\ge V_{\psi }^{{\pi }_{\psi }^{\ast }}\left(ϵ\right)-\epsilon$

Finally.^[9]

The basin of attraction. Now all that remains is to show that the conditions of Lemmas 1 and 2 can be maintained after updating. Informally, this is true as long as we can only receive a finite amount of evidence against ${\psi }^{{\pi }_S}$ at every step - in that case, a sufficiently large odds ratio $1-\delta :\delta$ for ${\psi }^{{\pi }_S}:\overline{\xi }$ will remain above $1-{\delta }^{\prime }:{\delta }^{\prime }$ up to time $T_{ϵ/2}$. By assuming $\psi$ deterministic, we ensured that percepts never provide evidence against ${\psi }^{{\pi }_S}$. The action chosen by ${\pi }_S$ are always of course consistent with ${\pi }_S$, but it will randomize between equivalent options (this is the trick that makes it rO-computable). It is possible for this to provide about $|A|$ bits against ${\pi }_S$ in the worst case (under the standard construction for ${\pi }_S$), though in expectation of course ${\pi }_S$ predicts itself best. That is where the condition (needed for the stronger result that ${\pi }_S$ remains $\epsilon$-optimal for all time) that only one action is Bayes-optimal for $\xi$ comes from. I assumed geometric discounting to ensure that $T_{\epsilon }^t$ does not depend on $t$, which could probably throw things off. Interestingly, if there were always two Bayes-optimal actions for $\xi$, the evidence against ${\pi }_S$ would be a kind of "$\xi$-randomness deficiency," which is the reflective-oracle analogue of M.L. randomness deficiency. So, the theory of algorithmic randomness has a connection to the basin of attraction for self-trust! This is a little unexpected - proper algorithmic information theory doesn't seem to come up in the theory of AIXI as much as you would expect.

This concludes the proof.

Closing Thoughts and Future Work

It seems to me that MIRI wanted to be able to embed an agent's code inside a larger piece of code and evaluate its performance. When everything is an rO-machine, this is totally possible. These machines are like... flexible lego blocks. You can snap them together however you want, but Observation 1 suggests that updating treats whatever structure you build this way like a weak suggestion. This means that the resulting agents may not have very dogmatic beliefs. I am not sure whether this is good. 

In this setting, self-trust has a "basin of attraction" which depends on non-dogmatically elevating the weight on a certain hypothesis. Playing with prior weights like this feels very clumsy. I think it would be nicer to build in knowledge through logical statements, perhaps using Hutter et al.'s (uncomputable) method for assigning probabilities to logical statements. If I understand correctly, this is vaguely related to the type of tiling properties Demski and his collaborators study in the computationally bounded setting using UDT. I am not satisfied with the current versions of UDT (and as explained above, I think there are good reasons to expect it is very hard to find a satisfactory theory of computational uncertainty). But of course rO-computability is not realistic and eventually we must move beyond this idealized setting.

I think reflective oracles are a reasonable model for agents of similar intelligence reasoning about each other or about agents of lower intelligence than themselves. This seems sufficient for modeling CIRL between idealized agents of equal power, which would be an interesting case to evaluate next.

 

1. ^{^}

   I've written more extensively about these complaints in many places, particularly here - but as long as you can make sense of this high-level intuitive description, you probably know enough to understand the rest of this post.

2. ^{^}

   Demski has called this the scratchpad problem, and is more or less solely responsible for convincing me of this point. 

3. ^{^}

   This is also the topic of Herrmann's PhD thesis, which is more philosophical and focused on action identification.  

4. ^{^}

   I realize this is a lot of jargon for one sentence. But I have to admit, there is something about uniting these ideas into something it would have been hard to formulate from scratch that I find pleasing. It makes the discussion feel more paradigmatic.   

5. ^{^}

   For AIXI, deliberation crowds out prediction.

6. ^{^}

   I am smuggling in a free exploration rate, which causes merging-of-opinions to do what I want it to, so that Lemma 4.17 of Jan Leike's thesis remains applicable after action selection. Informally, this avoids a divide-by-zero.

7. ^{^}

   The Self-AIXI paper is inconsistent about whether the policy distribution should be updated on the current action when comparing action-values. The intention seems to be to do so, and I follow this convention. 

8. ^{^}

   By expanding the value function $V_{\psi }^{{\pi }_s}$ in terms of the defining (arg)max's to arbitrary (finite) depth, we see the result dominates any finite-horizon value function, which can be shown equivalent to optimality at infinite horizon. 

9. ^{^}

   I have a feeling that someone better than me at measure theory (like Kosoy or Diffractor) could have done this proof so far backwards in heels and still taken half the lines.

Discuss