Published on July 19, 2025 12:26 PM GMT
by Yuxiao Li, Zachary Baker, Maxim Panteleev, Maxim Finenko
June 2025 | SPAR Spring '25
A post in our series "Feature Geometry & Structured Priors in Sparse Autoencoders"
TL;DR: We explore the intrinsic block-diagonal geometry of LLM feature space--first observed in raw embeddings and family-tree probes--by measuring cosine-similarity heatmaps. These diagnostics set the stage for baking block-structured and graph-Laplacian priors into V-SAEs and Crosscoders in later posts. Assumptions. tbd.
About this series
This is the second post of our series on how realistic feature geometry in language model (LM) embeddings can be discovered and then encoded into sparse autoencoder (SAE) priors. Since February, we have combined probabilistic modeling, geometric analysis, and mechanistic interpretability.
Series Table of Contents
Part I: Toy model comparison of isotropic vs global-correlation priors in V-SAE
➡️ Part II (you are here): Block-diagonal structures in toy LM activations
Part III: Crosscoders & Ladder SAEs (multi-layer, multi-resolution coding)
Part IV: Revisiting the Linear Representation Hypothesis (LRH) via geometirc probes
0. Background Story
Imagine walking into a library where every book—on wolves, quantum mechanics, and Greek myths—is piled into a single cramped shelf, pages interleaved and impossible to separate. This is the chaos of superposition in neural activations: too many concepts squeezed into too few dimensions. Traditional SAEs deal with the problem by demanding perfect orthogonality—like a librarian who insists each title stand ten feet apart—scattering lions and tigers to opposite ends of the building. In this post, we instead first map out the library’s natural wings—block-diagonal clusters of related concepts in LLM activations—so that when we design our SAE priors, we preserve true semantic neighborhoods while still untangling every hidden concept.
I. From Priors to Geometry: Why We Need to "Look Under the Hood"
Last week we kicked off this series with a dive into Variational SAEs (V-SAEs) and show: the ability to sculpt feature disentanglement via variational priors. On simple synthetic benchmarks, the vanilla SAE struggled to separate correlated latents, whereas a global-correlation prior dramatically purified fetaures. But one question remained:
What kind of prior should we choose if we want SAEs to capture the rich, categoircal geometry we actually see in language models?
Answering that requires exploring the true layout of the SAE's latent space and the model's raw embedding space. Only once we know how concepts cluster "in the wild" can we bake those patterns back into our priors--sharpening real semantic blocks and eliminating spurious overlap.
II. Related Work: Mapping and Manipulating Semantic Geometry
A growing body of work has begun to chart the geometry of learned representations--and to use that map to guide feature learning:
- Toy Models of Superposition (2022) introduced simple synthetic benchmarks illustrating the superposition phenomenon, while Decomposing LMs with Dictionary Learning (2023) first applied SAEs to LLM residual-stream activations, demonstrating that a learned overcomplete basis can uncover monosemantic feature vectors far more interpretable than individual neurons.The Geometry of Concepts: Sparse Autoencoder Feature Structure (2024) showed that single-token embeddings in transformers form local parallelograms (crystal structure) in the small scale, lobe-like clusteres (modular structure) in the meso scale, and power-law eigenvalue spectra in the large scale across layers (point-cloud structure).The Geometry of Categorical and Hierarchical Concepts in LLMs (2024) found that categorical clusters (e.g. animals, tools) carve out "polytopes" in activations space, with hierarchical substructured revealed by LDA projections.Hints of Universality in LLM Knowledge Graph Learning (2024) showed that different scales of LMs alike discover the same "gears" when learning relational structures--a powerful clue that we can probe, verify, and even transfer these universal internal representations across architectures with minimal adaptation.SAEs Do Not Find Canonical Units of Analysis (Meta-SAEs) (2024) showed that larger SAE latents decompose into combinations of smaller-SAE latents--demonstrating that SAE latents are not atomic and revealing how features can themselves be superposed.
Taken together, these works paint a picture: LLM feature spaces are neither randomly nor purely against orthogonally when presenting superposition--they exhibit structured geometry that we can and should exploit.
III. Propositions on Feature Geometry (Informal)
Before designing SAE priors, we posit three core hypotheses about how relational features arrange themselves in latent space:
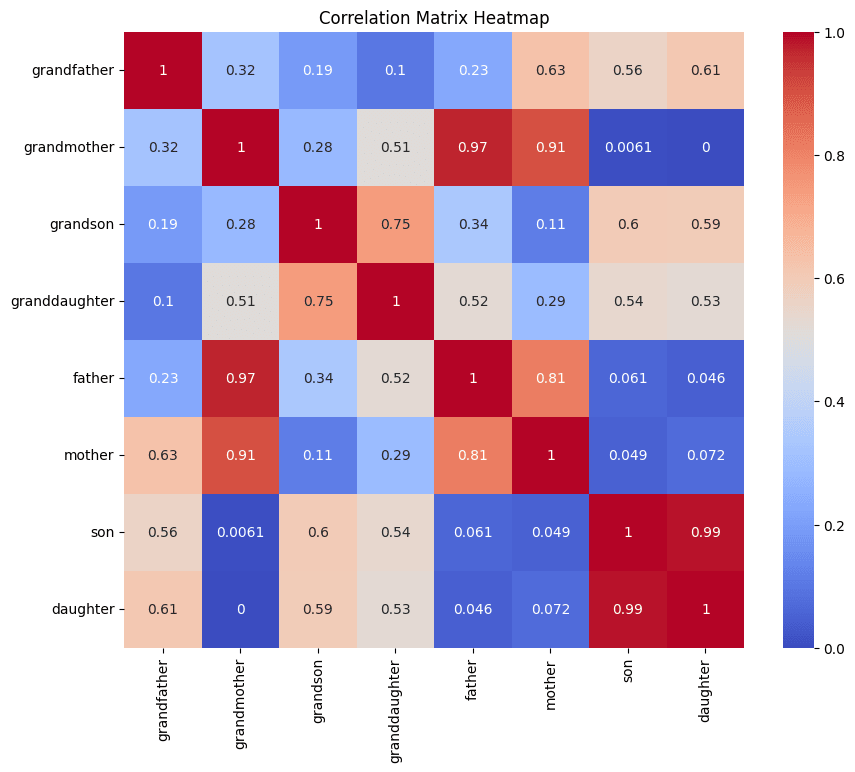
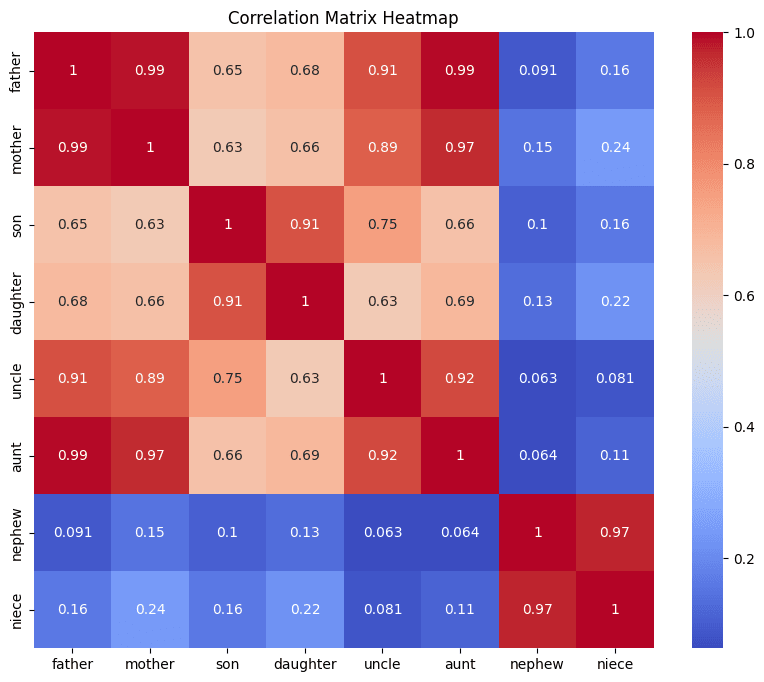
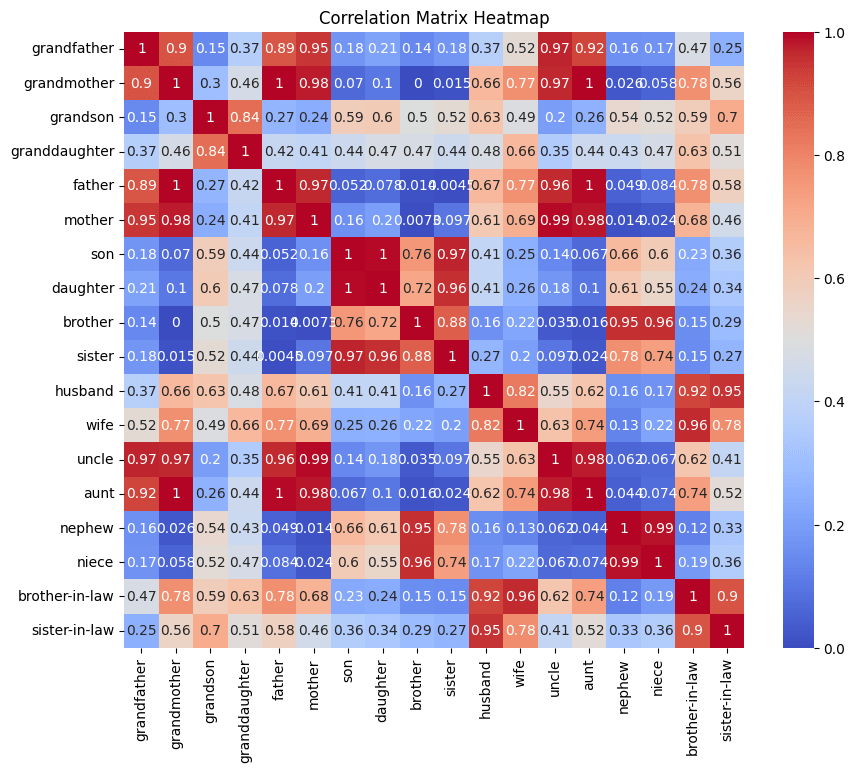
Informal Proposition 1 (Categorical Block-Diagonal Structure). Embeddings of relations from the same semantic category cluster together, yielding a block-diagonal pattern in the pairwise similarity matrix. Off-block correlations (across distinct categories) remain near zero.
Informal Proposition 2 (Hierarchical Sub-Clustering). Within each category's block, finer sub-relations form nested sub-clusters: a two-level hierarchy that can be revealed by removing global distractor dimensions.
Informal Proposition 3 (Linear Co-Linearity of Related Roles). Embeddings of semantically related roles lie nearly on a common line--or small subspaces--so that one can predict one embedding as a linear combination of another plus a small residual.
Finally, these observed patterns suggest a guiding principle for our next step:
Informal Proposition 4 (Geometry-Aware Priors Refine Features). If we can measure the latent geometry (blocks, hierarchies, co-linearity), then we can engineer V-SAE priors--via block-structured covariance, tree-based Laplacians, or hyperbolic priors--to align the learned dictionary with that geometry, avoiding artificial orthogonality and preserving true semantic continuity.
III. Empirical Structure Discovery
We tested Propositions 1-3 on synthetic family-tree embeddings in toy experiments.
- Block-Diagonal Correlation (Prop. 1)
- Method: Compute the 5×5 cosine-similarity matrix SijS{ij}Sij for relations , ordering indices by category (nuclear vs. in-law).Result: Two bright diagonal blocks (mean intra-block ≈ 0.72) and faint off-block values (mean ≈ 0.18), confirming clear categorical separation.
- Method: Project out global distractors via LDA, then run t-SNE on the 64-dim codes and apply spectral clustering within each block.Result: Within the “nuclear family” block, three tight sub-clusters emerged matching , and similarly distinct sub-clusters in the in-law block once distractors were removed.
- Method: Fit a linear regressor from <span class="mjx-math" aria-label="[z{\rm parent},\,z{\rm sibling}]"> to predict <span class="mjx-math" aria-label="z{\rm uncle}">.Result: Achieved MSE ≲ 1 (vs. ≳7 for random target), demonstrating that “uncle” embeddings lie in the span of “parent”+“sibling.”
IV. From Geometry to Prior Design
Our key insight:
"If we can measure structure in latent space (blocks, hierarchies, co-linearity), we can engineer priors to match that structure--using KL-divergence or graph regularizers to guide SAE learning accordingly."
Concrete next-step priors:
- Block-Structured Gaussian Covariance.
with intra-block correlation ρ\rhoρ.Tree-Laplacian Regularizer.
Build a small family-tree graph , compute its Laplacian , and add to encourage activations to vary smoothly along known edges (parent–child vs. sibling).Hyperbolic / Poincaré Priors.
For truly hierarchical relations, a hyperbolic latent prior naturally embeds tree distances and can be plugged into a variational framework (e.g. Poincaré VAE).
These geometry-aware priors will form the backbone of our Part III experiments, where we deploy V-SAEs and Crosscoders on real LLM activations—enforcing the semantic blocks and hierarchies we have now fully characterized.
Discuss

