本文深入浅出地介绍了博弈论中的经典案例——囚徒困境。通过模拟犯罪情境，详细阐述了囚徒困境的基本设定、决策过程及纳什均衡。文章指出，尽管双方理性选择导致的结果并非最优，但囚徒困境揭示了自我利益与集体利益之间的冲突。随后，文章预告了对囚徒困境在现实世界中的适用性进行探讨，并思考博弈论是否需要寻找更贴近实际的案例。

🤔 囚徒困境的核心在于：两名同伙被捕后分别接受审讯。警方缺乏足够证据，若双方均保持沉默，则只能因盗车罪被判一年。警方试图通过提供减刑来诱导一方背叛对方，从而使背叛者免于监禁，而对方则面临五年刑期。

🤝 囚徒困境的决策矩阵揭示了博弈的复杂性。玩家面临合作（保持沉默）或背叛（坦白）的选择。从纯粹的个人利益角度出发，背叛总是更优选择，因为无论对方选择如何，背叛者都能获得更短的刑期。

⚖️ 纳什均衡是囚徒困境的关键概念。在这种均衡下，任何一方单独改变策略都无法改善自身处境。然而，囚徒困境的纳什均衡（双方背叛）并非帕累托最优，即并非对双方来说都是最好的结果。

💡 帕累托效率强调，在不使任何一方更差的情况下，无法使任何一方变得更好。囚徒困境中的帕累托最优解是双方合作。囚徒困境的“困境”源于自私的纳什均衡与对双方都有利的帕累托最优结果之间的冲突。

Published on July 2, 2025 7:10 PM GMT

The Prisoner’s Dilemma is the go-to example for game theory noobs and experts alike. It’s a non-zero-sum game that introduces payoff matrices, it has a Nash Equilibrium that is not also Pareto Efficient (helping to distinguish between the two) and when taken further, we discover that strategies change with iterated games. It’s got it all! Or does it? This post explains the Prisoner’s Dilemma and details its benefits while the following series will question whether or not it’s really the best advocate for game theory in the real world.

The Premise

You have just robbed a bank. You’ve cracked the safe, packed the money bags, jumped in your getaway car with your partner, and sped off down the highway, only to find yourself tailed by the cops. As you weave through dark back streets, you hurl the money bags out the window to avoid being caught with the evidence. But alas, eventually you reach a police cordon and screech to a halt. The jig is up—you and your accomplice are arrested and taken in for questioning.

The Dilemma

The Prisoner’s Dilemma involves the separate interrogations of you and your partner. The cops don’t have enough evidence to put you away for robbery. If you and your partner are loyal to each other (by staying silent), the cops can only nab you on the stolen car, which is 1 year. So they are trying to make you rat out your partner, by offering leniency—if you do rat out your partner you’ll get no jail time, and your partner will get 5 years.

This is already a dilemma, because if you have any loyalty to your partner, getting 2 years between you is better than one of you getting 5 years! On the other hand, you have the chance to avoid jail altogether. But it gets more complicated, because this deal is not only being offered to you, but to your partner too… meaning that if you cooperate and they rat youout you’ll get 5 years and they’ll get off scot-free. If you both betray each other, then you both get convicted, but also both get leniency—2 years each.

We represent this in Game Theory by using a payoff matrix.

You have two choices: cooperate and get 1 year if your partner also cooperates or 5 years if they don’t, or defect and get 0 years if your partner cooperates, or 2 years if they don’t. In terms of pure self-interest, you will always be better off defecting—0 is better than 1 year, 2 is better than 5 years, and this is amplified by the fact that the same is true for your partner (making the possibility of them defecting and you getting 5 years a very real one). In Game Theory this is called a Nash Equilibrium.

Nash Equilibrium

When no player can improve their position by unilaterally changing their strategy.

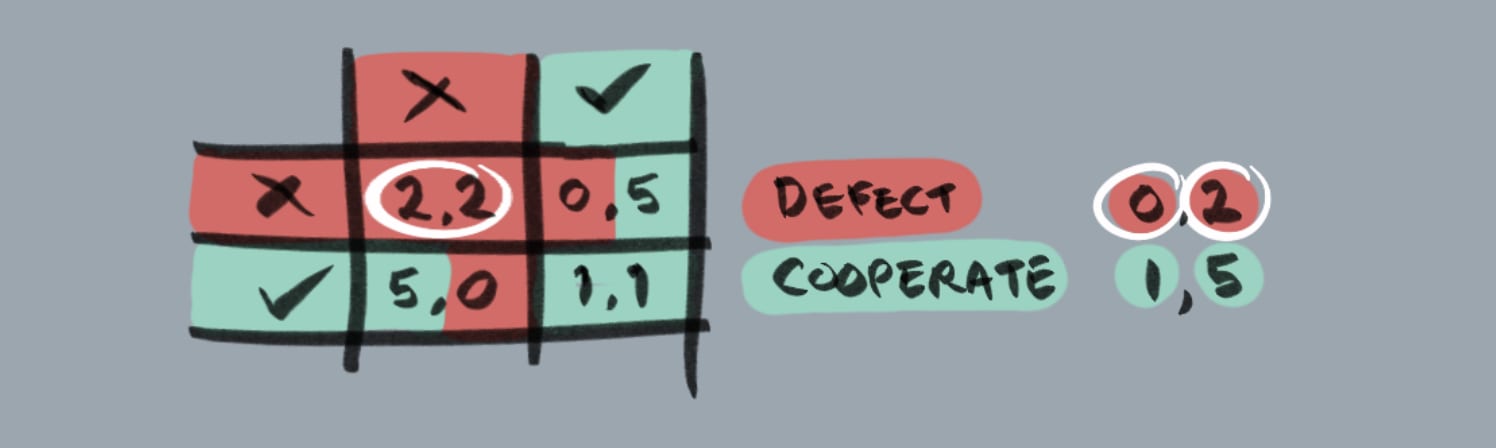
The Nash Equilibrium for the Prisoner’s Dilemma is mutual defection, because there is no situation where diverging from this path benefits the player. But, if the answer is so clear, why is it a dilemma? And why does it feel so wrong???

Well, that’s because, although the dominant strategy is clear, the result is sub-optimal: if both parties defect, they get a worse payoff (2,2) than if they had both cooperated (1,1). In Game Theory terms, the Nash Equilibrium is not Pareto Efficient.

Pareto Efficiency

When there is no way to make any one player better off without making at least one player worse off.

Thus, the Pareto Efficient solution for the Prisoner’s Dilemma is mutual cooperation. The “dilemma” in the Prisoner’s Dilemma arises from the conflict between the Nash Equilibrium, driven by self-interest, and the Pareto Efficient outcome, which benefits both players.

So...

Is there a solution? In the next part we will explore how the Prisoner’s Dilemma applies (or fails to apply) in the real world and see how iterated games change the dominant strategy, better reflecting our moral intuitions. We’ll look at the limitations of contained one-shot games, and the idea of “rational” actors, and ask “Is the Prisoner’s Dilemma ultimately a force for good in the world, or could the field of Game Theory find another poster-child?”.

This series of posts will look at candidates that better reflect, and are more positively applicable to, the real world.

---

Notes

For more detail on the concepts touched on in this post check out our posts on Nash Equilibrium and Pareto Efficiency.If you’re interested in learning about repeated games, there will be more in this series, but for now check out Jaiveer’s post on repeated games.

Discuss