本文深入探讨了大型语言模型（LLM）中起始标记（bos_token）的特性，该标记在序列开头被添加，其激活值远高于其他标记，并吸引大量注意力。研究通过可视化分析，揭示了bos_token在GPT2 Small、Gemma 2-2b和Llama 3.2等模型中的大规模激活现象，以及其与查询-key潜在空间的关系。文章还探讨了干预bos_token激活对模型的影响，并分析了其在MLP中的作用，旨在帮助读者深入理解LLM的内部机制和关键组成部分。

🧐 **bos_token的突出表现**: 在LLM中，bos_token的激活值远高于其他标记，成为吸引注意力的“汇聚点”，例如在GPT2 Small、Gemma 2-2b和Llama 3.2中均有体现。

💡 **关键方向的对齐**: bos_token的大规模激活对应于查询-key潜在空间中的特定方向，后续位置的大部分查询都与此方向对齐。

⚙️ **MLP权重的作用**: bos_token的激活增长主要由MLP的权重驱动，在MLP输出权重矩阵和偏置中，维度447与激活对齐，表明存在增加残差流中维度447的梯度压力。

Published on June 17, 2025 7:00 PM GMT

LLMs process inputs as a sequence of tokens. Typically, a dummy token is prepended to the sequence, known as the bos_token (beginning of sequence token). 

Input: "Good morning" 

Token strings: ['<|bos_token|>', 'Good', ' morning'] 

Tokens: [50256, 10248,  3329]

Though the bos_token passes through the same MLP and attention weights as all other tokens, it exhibits distinct emergent behavior. Its activations are several orders of magnitude larger than other tokens, and it often receives over 50% of the attention from downstream positions.

Why is this token so critical? What drives this emergent behavior, and does it indicate architectural constraints of the model, or fundamental properties of language? These are all questions that researchers have asked and investigated heavily already. This post provides a walkthrough of emergent properties of this token, with an emphasis on visualization to promote curiosity. I am not an LLM expert, but hopefully exploration, discussion, and feedback can help me (and others) deepen our understandings of model internals.

To that end, in this post I:

Visualize properties that have been well documented in literature: massive activations on a small number of dimensions, attention sinks, and specific l2norms across 3 open source models.Show that the massive activation in the bos_token corresponds to a distinguished direction in the query-key latent space. The vast majority of queries for later positions across all layers and heads align with this direction. Step through the parameters that generate the massive activations, and show how these same parameters have downstream effects. Perform training runs where I ablate the model architecture around the bos_token to introduce a token-specific override, enabling the MLP weights to no longer devote parameters to setting the attention sink.

Github source code: https://github.com/ClassicLarry/curiousCaseBosToken 

Related Works and Background

For brevity, I assume familiarity with transformers and the attention mechanism. Some relevant terms:

Attention Sinks. Positions with low semantic meaning that attract a disproportionately high amount of attention, often >50%. (Xiao et al., 2024^[1])Massive Activations. Activations with substantially higher values (x10^5) that function as attention sinks, also referred to as indispensable bias terms. (Sun et al., 2024^[2])

When optimizing streaming applications, Xiao and others observed that inference performance collapsed once the first several positions left the key cache, as these positions were functioning as attention sinks. Updating training and inference with a consistent dummy bos_token improved performance and functioned as an attention sink.

The bos_token attention sink is hypothesized to function as a stable no-op to prevent overmixing and  forms gradually over 10,000+ training steps in Llama 2 style LLMs (Barbero et al. 2025^[3]). Attention sinks also occur in simple 1-3 layer attention models trained on the Bigram-Backcopy task (Gu et al.  2024B^[4]). Even in the presence of rotary positional embeddings, the bos_token still serves as a reliable attention sink via low frequency bands (Barbero et al. 2024^[5]). 

The following models explored in this post.

	GPT2 Small	Gemma 2-2b	Llama 3.2 3B
Params	124M	2B	3B
Layers	12	26	28
Heads Per Layer	12	8	24
Vocab Size	50257	256000	128256
Model Dim	768	2304	3072
Head Dim	64	256	128
MLP Dim	3072	9216	8192
Linear Bias	Yes	No	No
Attn Type	Standard	Alt global/local by layer.  Grouped Query Attention	Grouped Query Attention
Normalization	LayerNormPre	RMS Norm Pre and Post	RMSPre
Positional Embed	Absolute	Rotary	Rotary
MLP Type	Standard	Gated	Gated

 

Massive Activations on the bos_token

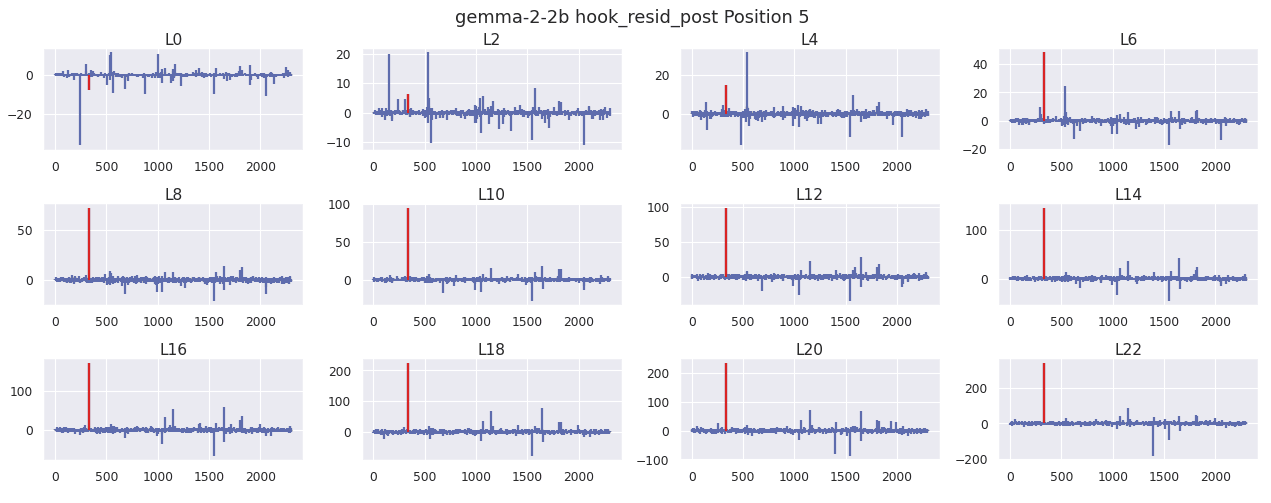
GPT2-Small, Gemma-2-2b, and Llama 3.2 all show massive activations form on the bos_token. This is plotted below, where the x axis of each plot is the model dimension of the residual stream.

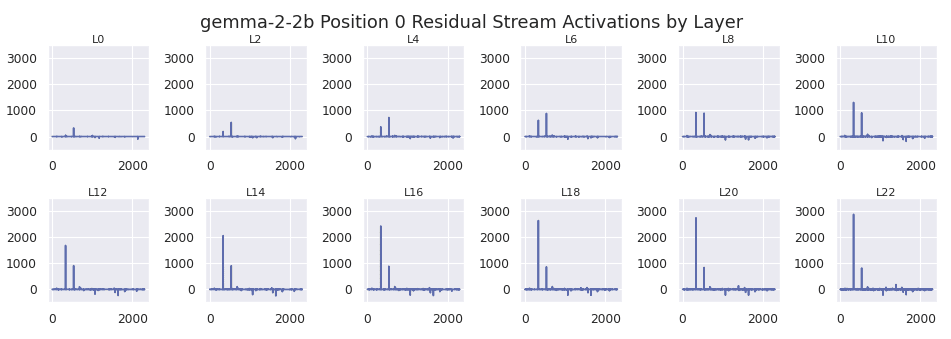
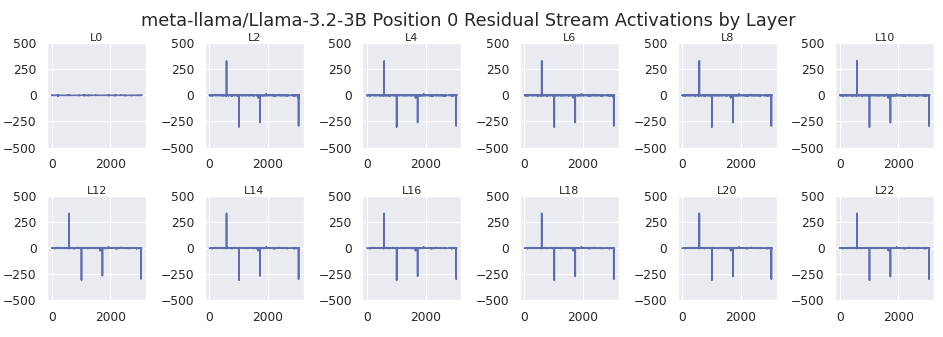
This is in sharp contrast to later positions, which typically have activations 2 orders of magnitude smaller. As an example, I use the short prompt "The sale ends today. You won't want to miss it!". This prompt is used for all subsequent analysis unless specified otherwise. A sample is shown below for GPT2-small, where the bos_token position is highlighted in red. Each y axis starts at 0.

To check for the existence of an attention sink, I plot the average causal attention patterns for each layer of all 3 models. The shade of each (row,col) corresponds to the attention tokens[row] assigns to tokens[col].

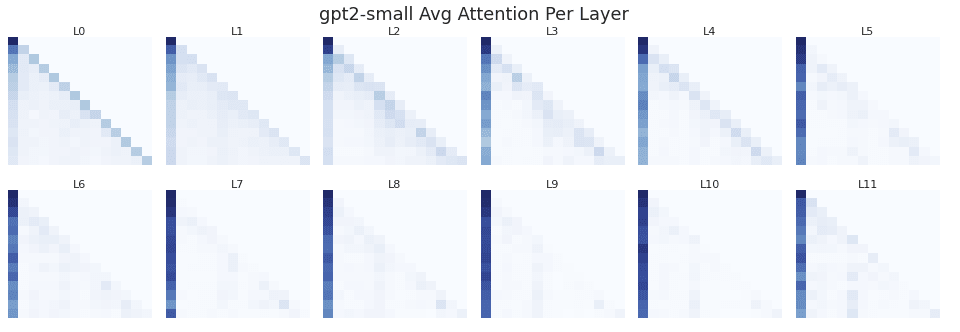
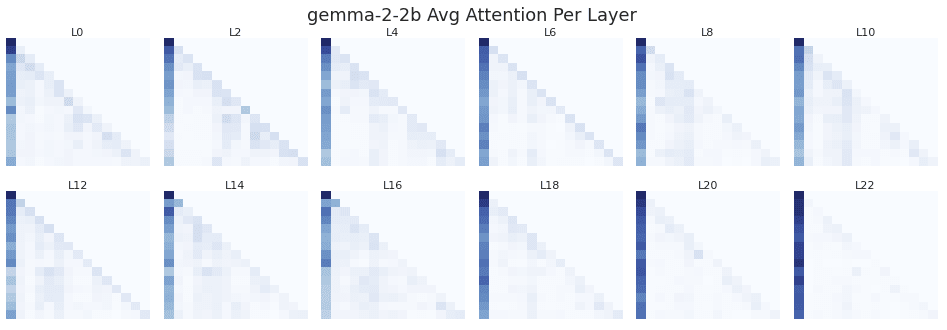
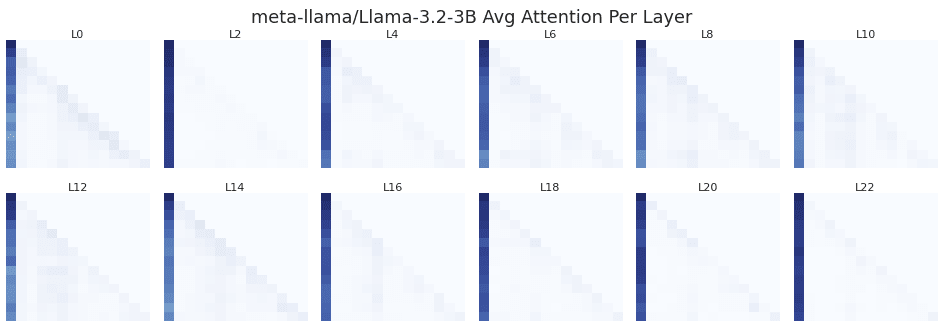
Llama 3.2, which has 3x more heads per layer than Gemma 2, shows substantially more attention placed on the bos_token on average.

Intervening on the Massive Activation [GPT2-Small]

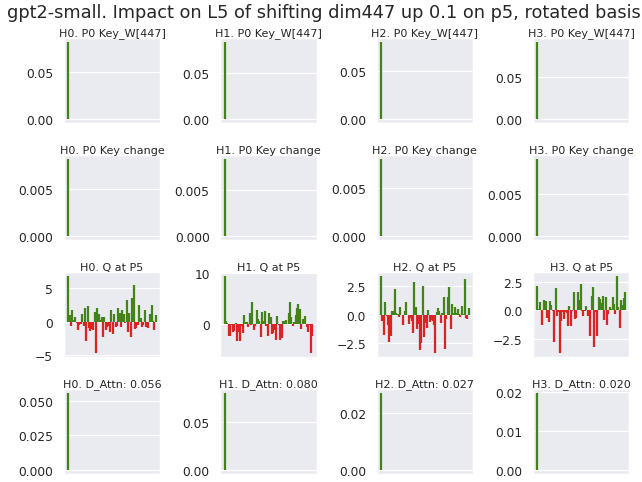
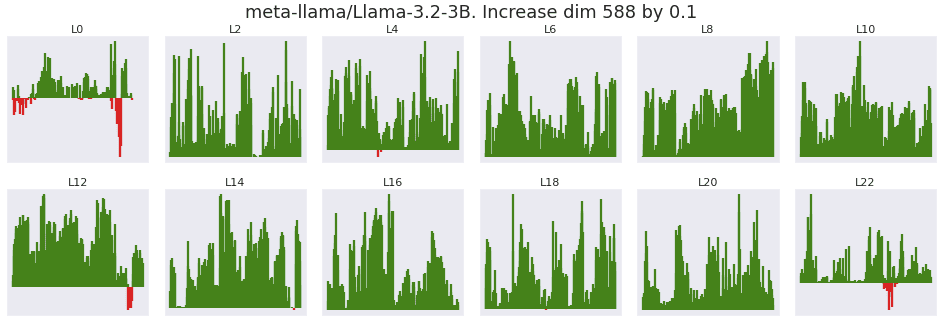
Prior researchers have experimented with setting massive activations to zero and observed performance collapse (Sun Et al 2024^[2]). Here I test scaling the residual stream massive activation at its strongest dimension up and down by a fixed increment of 0.1, directly after normalization^[6]. The x axis of each plot is a flattened version of each downstream position and head. The y axis is the change in attention given to the bos_token, with positive changes colored green.

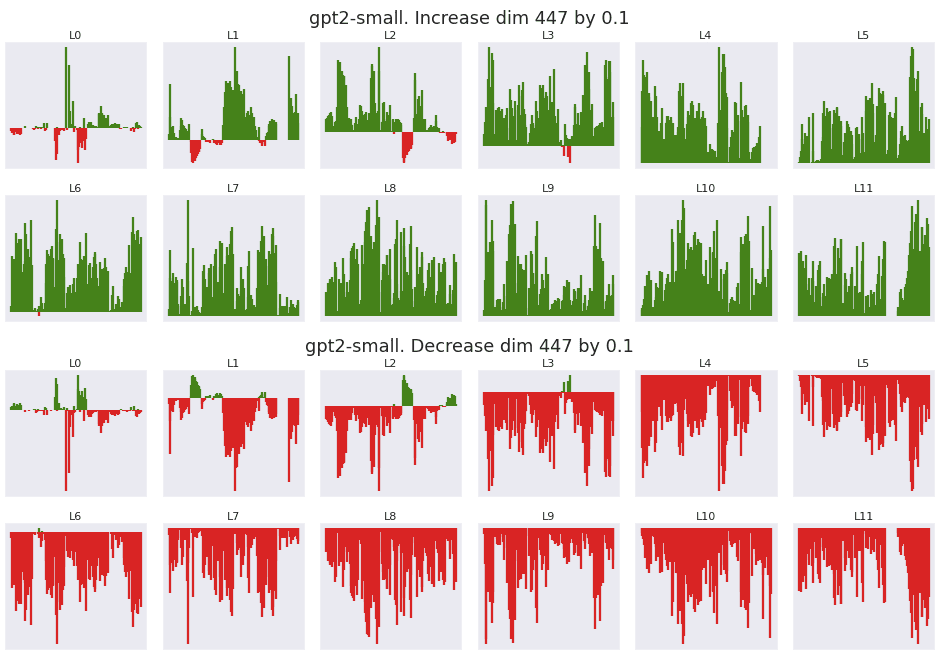
From layer 4 to layer 11, 99.9% of all heads and positions see an increase in attention given to the bos_token when the massive activation at dimension 447 is scaled upwards. As expected, decreasing the massive activations shows the inverse result.

How is the alignment between the massive activation and the attention is so consistent? Specifically, why is the dot product almost always positive between the bos_token key and downstream queries? First I validate that the post normalized values prior to the attention mechanism exhibit the same distribution.

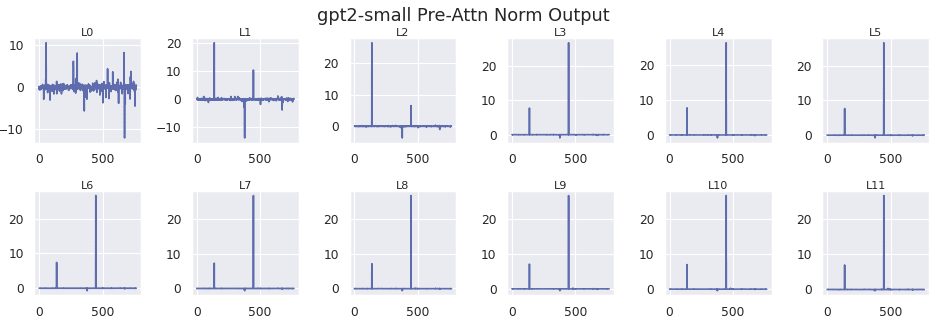
These charts confirm that the layer norm is simply scaling the activation down by a factor of roughly 100. To investigate the change in attention, I plot 4 rows below for the first 4 heads in layer 5, for the attention between the bos_token key and the query from position 5.

The key weight matrix at index 447.The change in the key induced from intervening. Shows a scaled version of row 1.The query at position 5.The attention change from multiplying the key change with the query

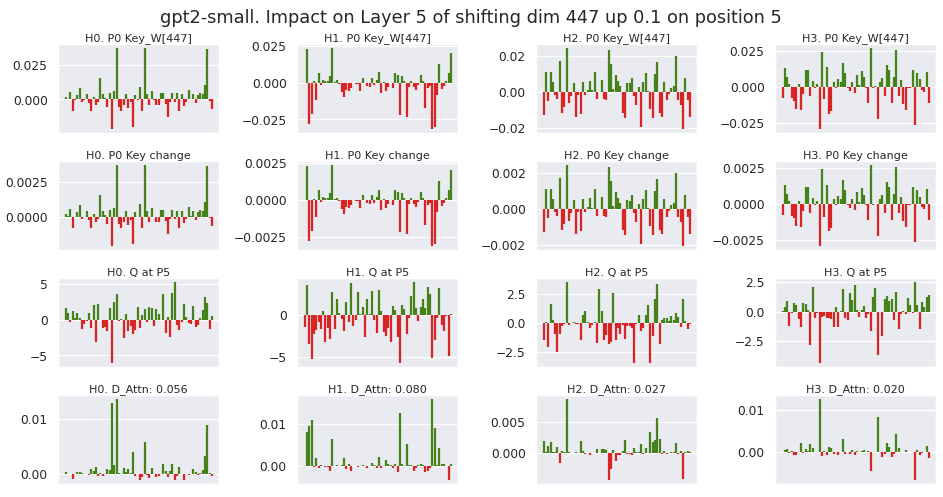
These charts indicate that the sparse residual dimension- which gives a clear importance to dim 447- is being smeared out across all 64 dimensions of the head latent space. To improve the interpretability of the head latent space, I rotate the key-query latent space such that Key_W[447] rotates to the value [1,0,0,...].

After performing this rotation, I then visualize the orientation of every query across every layer and head below. The x axis of each plot is the direction K_W[layer, head, 447], and the y axis is an arbitrarily sampled orthogonal direction. Each blue line corresponds to the query generated at a unique position in the sequence. Each query is scaled to norm 1.

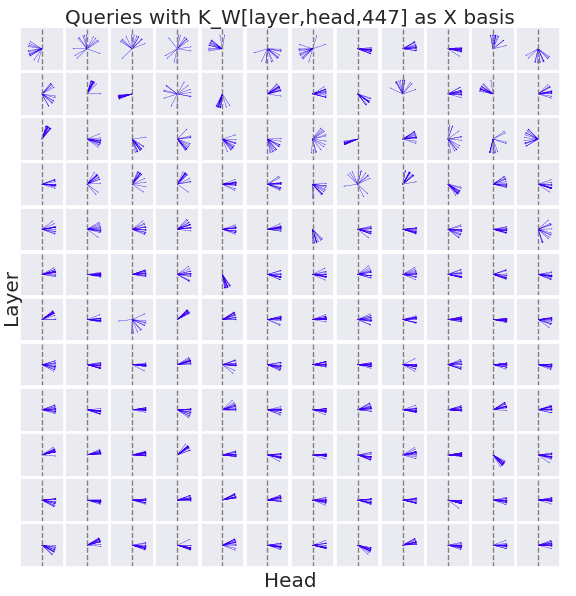
The queries from layers 4 onwards almost universally have a positive dot product with the key weight at the dimension 447, and as a result point to the right.

I then repeat with the longer prompt "There once was a traveler named Joe who had been to every country in the world. He kept a journal of his adventures. He knew many languages and had tried many different cuisines. When Joe reached the old age of 96, he died. The end.".

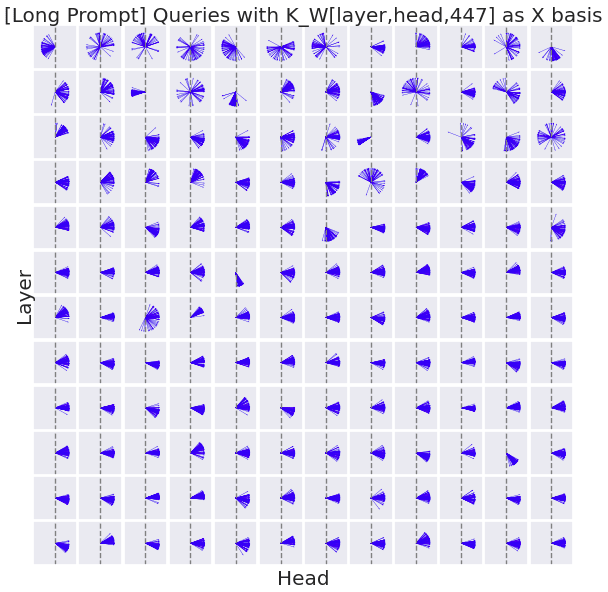
A similar pattern is observed. Next, I return to the shorter prompt and plot the queries with a basis of K instead of K_W[447]. 

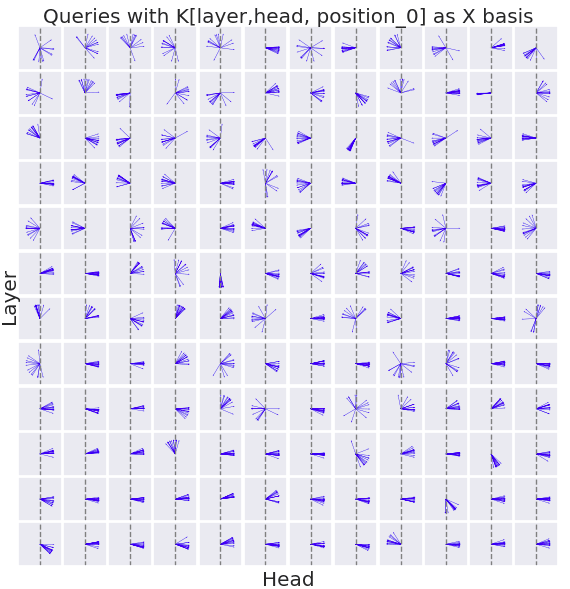
This plot shows an interesting divergence- suddenly a large number of heads are no longer aligned with the basis. For instance, layer 7 head 0 shows the majority of queries having a negative dot product with the key. 

The chart below isolates the cause of this divergence, by comparing the key, key without a bias, key from only dim 447, and the alternative key from the position that generates the next highest attention. For each item, the l2norm and resulting attention logit is shown. 

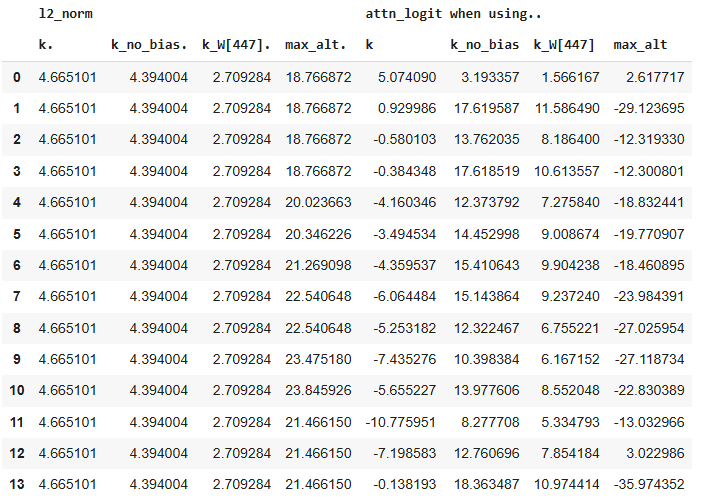
The attention logit only becomes negative once the bias is applied to the key. The l2 norm of the key at position 0 is substantially smaller that the l2 norm of later positions. As a result, position 0 is more heavily influenced by the bias term of the key. The fact that other keys have such higher l2 norms, but still fail to create higher attention logits indicates that they have large angles with the majority of queries.

This observation prompts me to plot the other keys along this same basis.

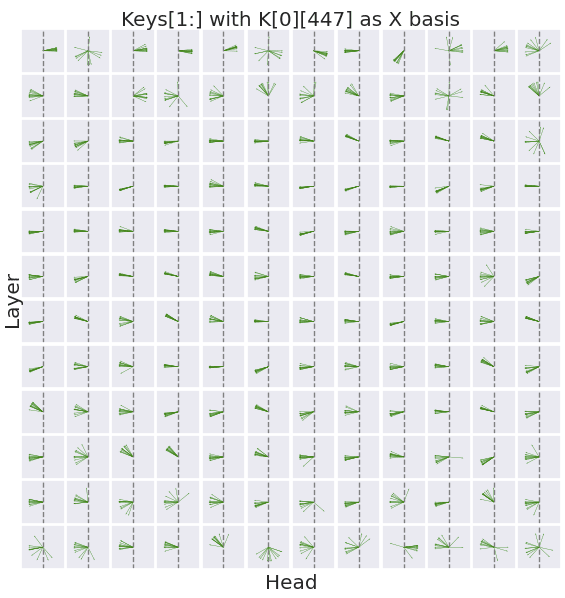
Interestingly, the keys for later positions almost universally form a negative dot product with the basis k[0][447]. To confirm this trend from another angle, I shift the X axis basis to the key of the position after the bos_token.

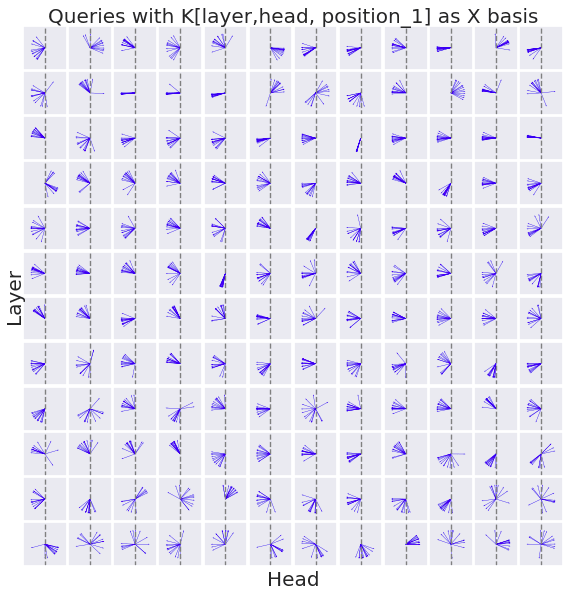
This chart appears to confirm that the queries are specifically orienting to the basis of the massive activation of the bos_token, and away from the keys at later positions.

The previous observations on the l2norms were just with respect to layer 7 head 0. The following charts show the L2 norms across each layer, head, and position for every key and value. Each y axis starts at 0, and the bos_token is highlighted in red. 

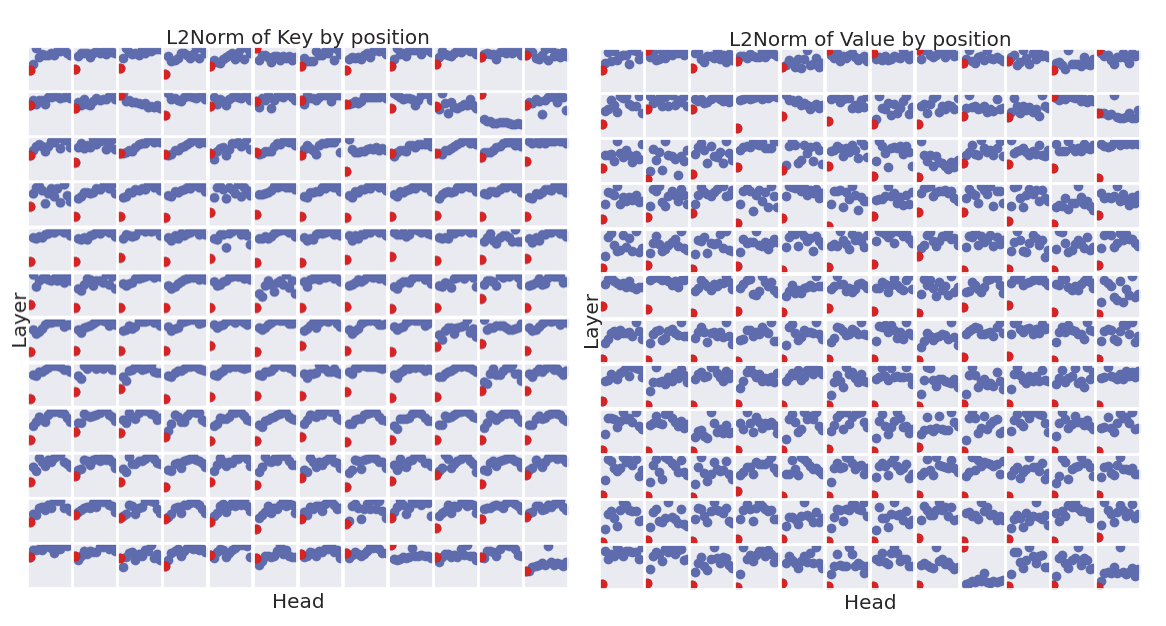
The charts show that the l2norms of the key and value at the bos_token are substantially lower than other positions during the intermediate layers. 

 

Investigating the cause: MLP Weights [GPT2-Small]

I first show the growth of dimension 447 over the course of each attention and MLP layer.

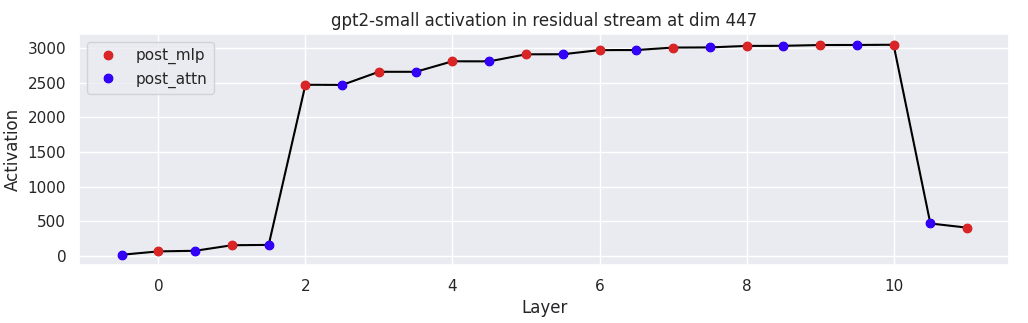
The increase is driven by the MLP in layer 2. The progression from the residual stream, through layer norm, the MLP hidden dimension, and the nonlinear activation is shown below.

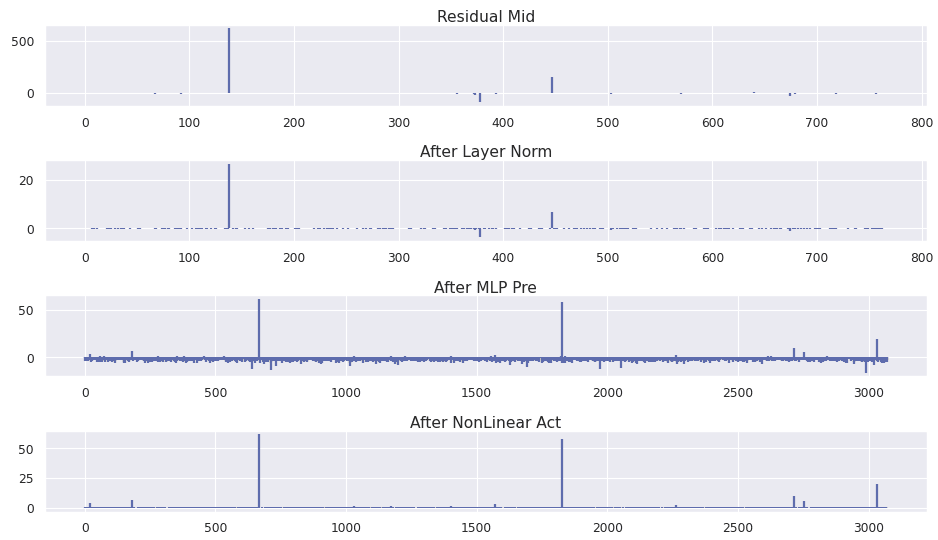
Interesting, the activation maintains a sparse representation in the MLP dimension. Next, the MLP out weight matrix and bias are applied.

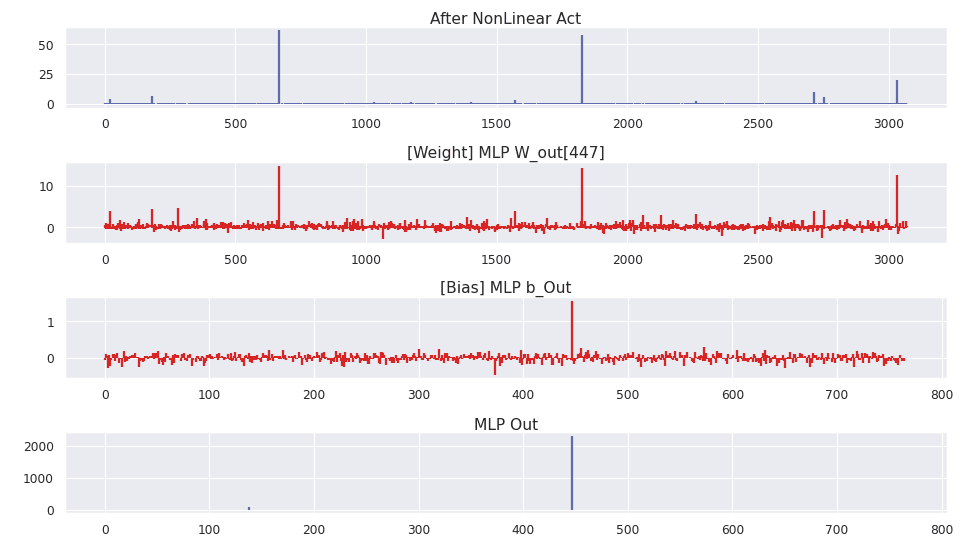
The weight matrix at dimension 447 shows clear alignment with the activation, as well as the model bias. To see these large weights despite the presence of weight decay indicates that there is substantial gradient pressure to increase dimension 447 in the residual stream.

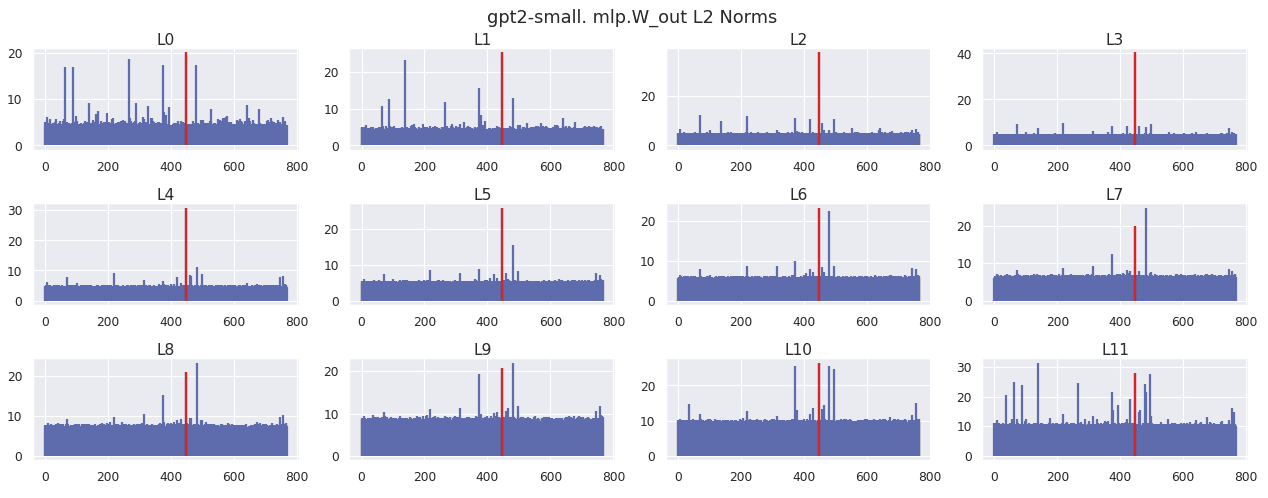
The chart below shows the l2norm of every dimension in the MLP out weight matrix. Dimension 447 is highlighted in red. 

The bias at every layer for the MLP out is shown below. Dimension 447 is highlighted in red.

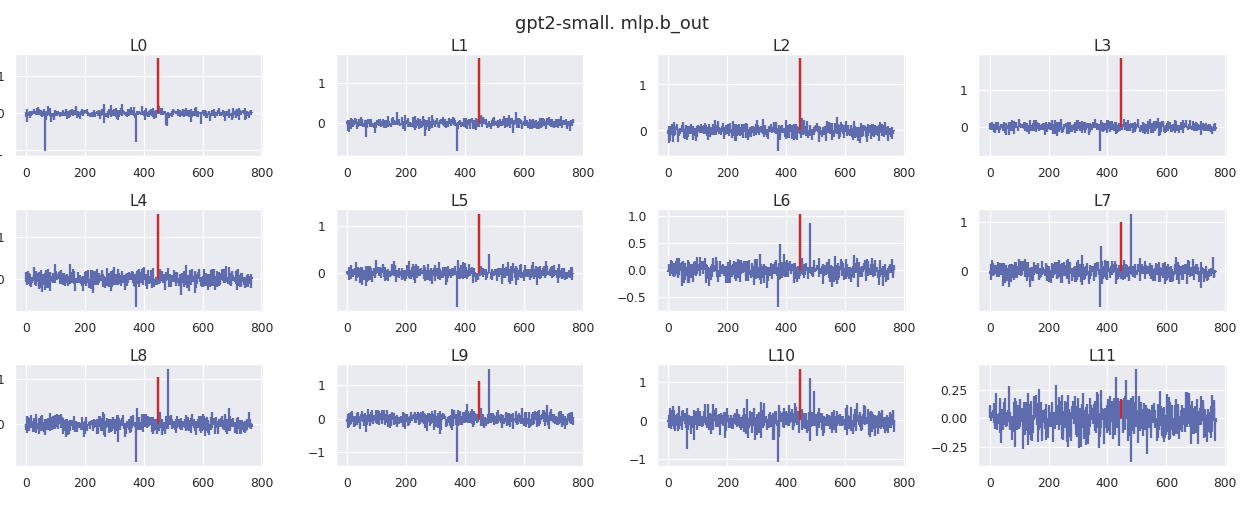
What I find peculiar about this behavior is the same weights and biases are getting used at every position, yet the need to create this attention sink only applies to the first position. As a result, there is a single set of weights that need to accomplish two objectives that appear quite different. When I look at the residual stream for position 5 and 9, I can see that the shared weights of the MLP are pulling up dim 447.

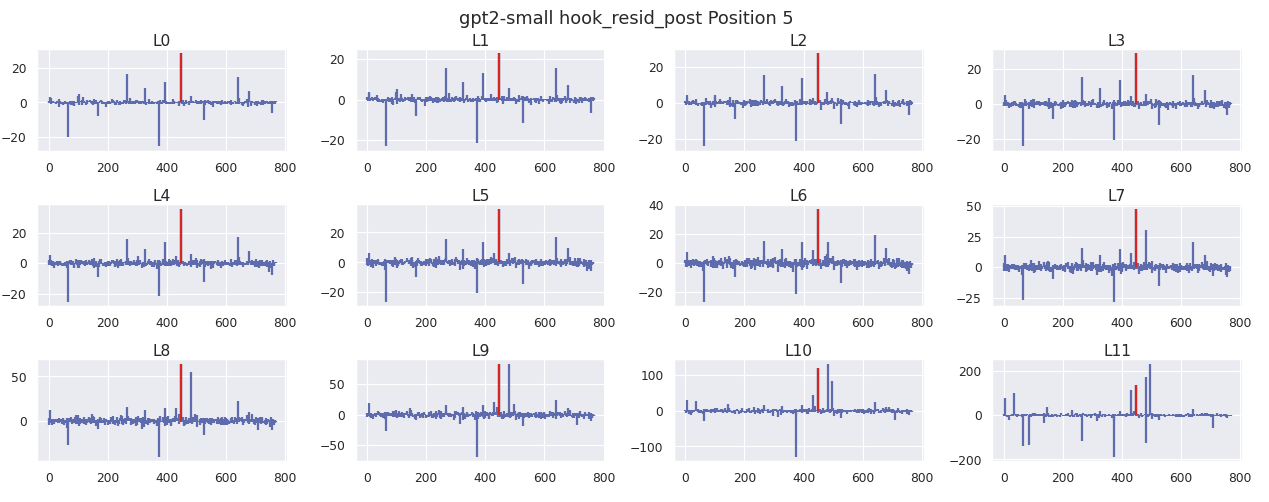
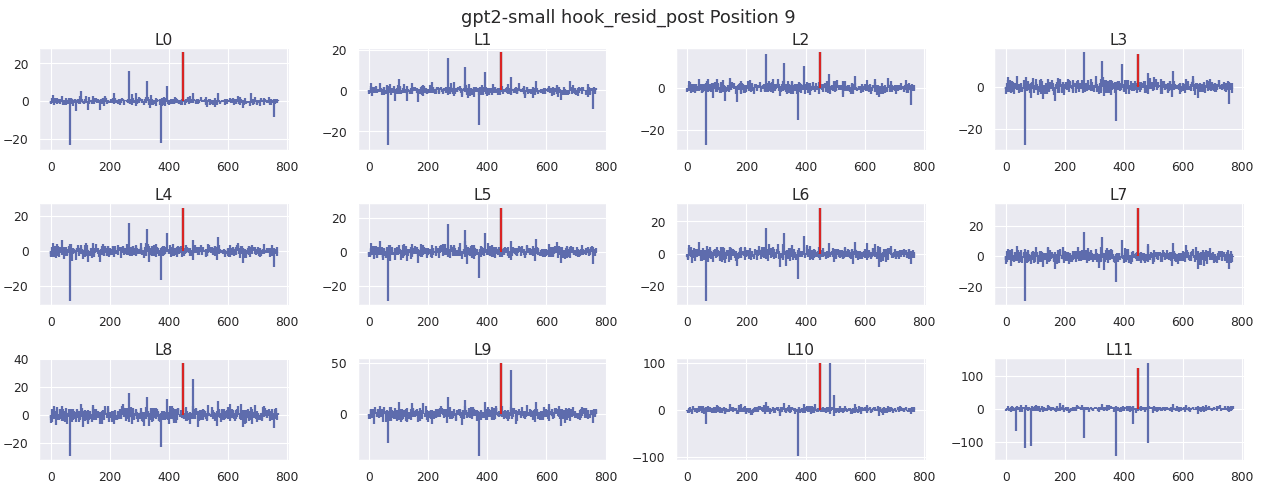
The position 5 residual stream looks surprisingly similar to the position 9 residual stream. To investigate this further, I plot the cosine similarity of every position in the residual stream at each layer.

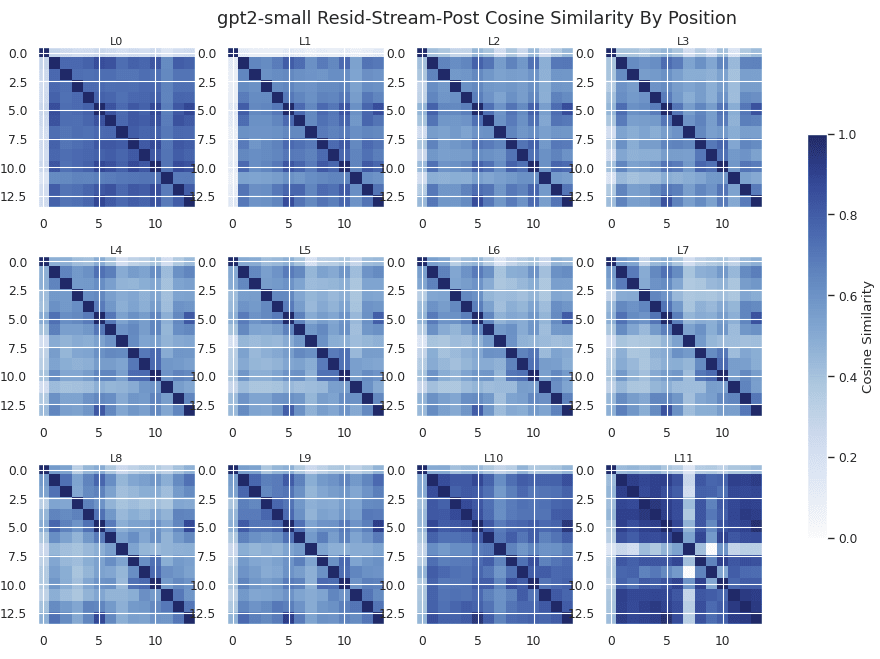
Given that the residual stream has a dimension of over 700, a cosine similarity of over 0.5 is remarkable. This helps partially explain why the queries are able to behave so consistently with respect to the basis K_W[447]- they all sit on a relatively small manifold of the latent space. Position 7 in Layer 11 shows low cosine similarity. This token refers to the position at the end of "The sale ends today. You wo" just before "n't want to miss it!" Presumably, at this point the model has extremely high confidence that "n't" follows, whereas generally the latent sits in a more standard distribution.

 

Expanding to Gemma2 and Llama 3.2

The linked github repo above contains the full list of plots. The notable similarities and differences from GPT2-Small are shown here. 

Both Gemma2 and Llama 3.2 show the same trend of increasing bos_token attention when the massive activation is increased after the normalization and before the attention layer.

 

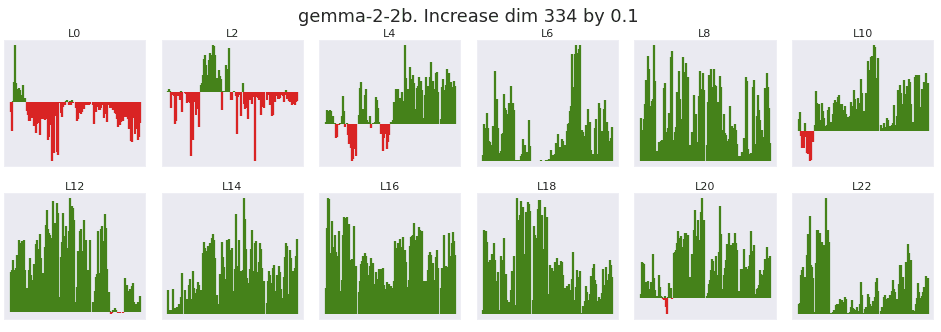
The progression of the massive activation in Gemm2-2B is gradual across every layer, instead of sudden as seen in GPT2-Small.

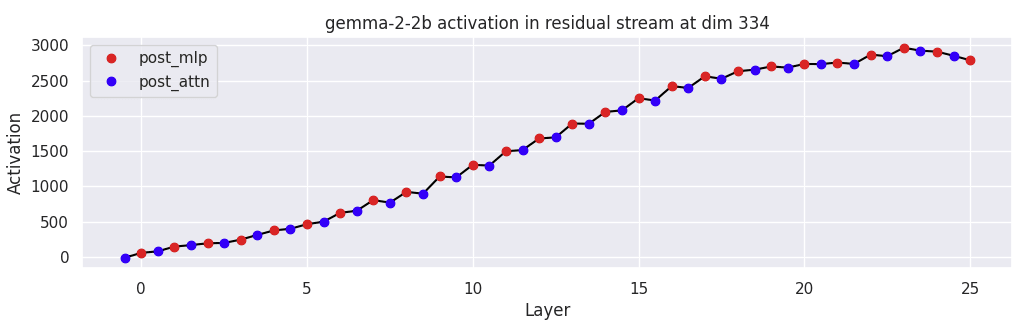
Speculation: This may be driven by the fact that Gemma2 has a post normalization step before adding back to the residual stream, thus requiring many more layers to drive an activation up to 3,000. 

After downscaling via root mean squared normalization, the post normalization step applies a rescaling of the output. Dimension 334 is highlighted in red, which is typically scaled up by a factor of 6 at every layer.

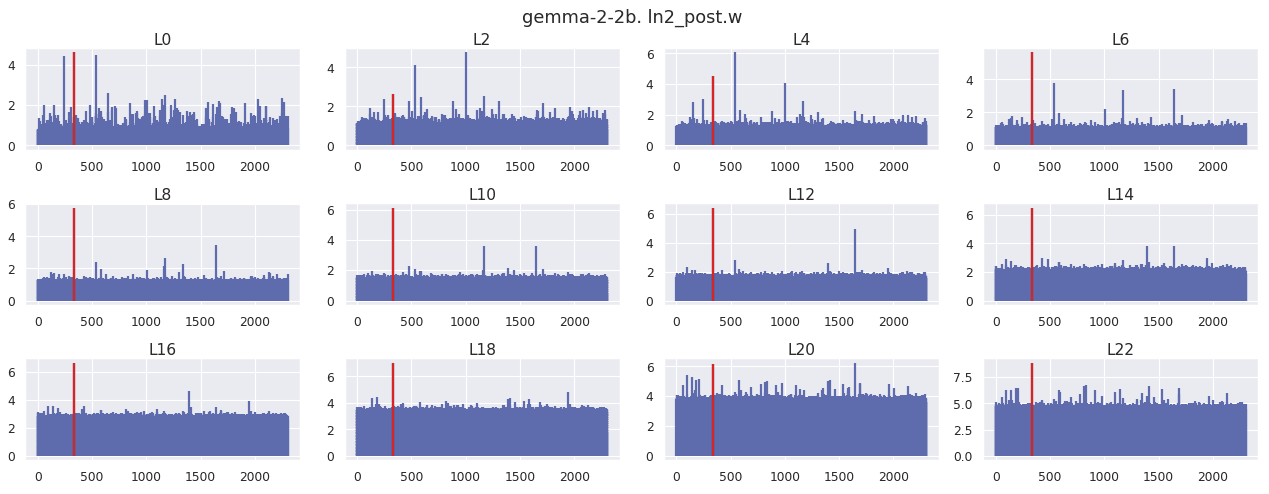
This scaling factor is shared across all positions, which means other positions exhibit some additional activation of dimension 334. This is shown below for position 5.

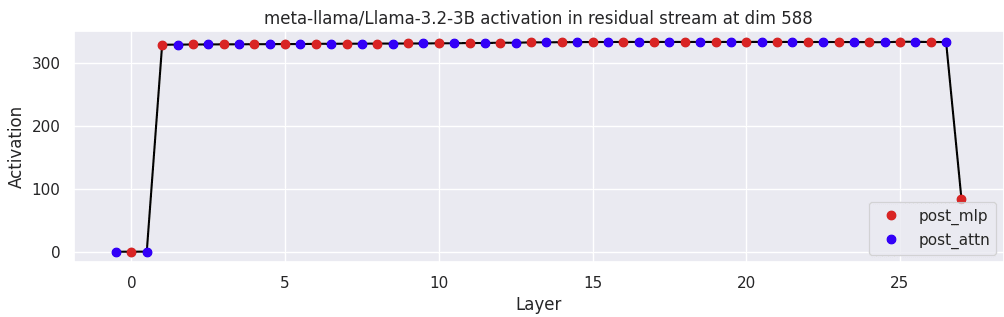
The progression of the massive activation in llama3.2 occurs very suddenly in the layer1 MLP, and doesn't reach the scales seen in GPT2 or Gemma2.

 

Ablating the Model Architecture

Speculation: transformers do not appear to have a clean way to perform a contextual no-op during attention. As a result, a dummy token gets added to the start of the sequence, which the model must then learn to manipulate to perform a very specific function, using the same weights that it uses to model language interactions for every other position. It may be that performing this dual function with the same set of weights is an effective form of regularization, or a way to sync the key and query manifold, but it is not obvious to me that this is the case. As a result, it appears worth experimenting on separating these functions.

As a first pass modification, I experiment with a learnable parameter of size (d_model) dubbed 'bos_override', which I add to each block in the transformer architecture. This override parameter replaces the residual stream at the bos_token after the execution of the MLP layer. Each block is given its own parameter. The intent here is to prevent the MLP weights from needing to set the attention sink key and values. Prior research has explored adding key biases to reduce massive activations, but to my knowledge this was done uniformly across all positions, instead of just the bos_token- though there are certainly many experiments in this space I am unaware of.

As done in Llama 3.2, I perform intra-document masking to remove any cross document complications. An A100 GPU is used through Google Colab for each training run. https://github.com/karpathy/nanoGPT is used as a starting point for training optimizations. Flex attention is added for optimizing intra-document masking. The following experiments are ran:

Train GPT2-Small from scratch (baseline)Train GPT2-Small from scratch with intra-document masking (baseline)Train GPT2-Small from scratch with intra-document masking and bos_overrideTrain GPT2-Small from hugging face pretrained checkpoint with intra-document masking (baseline)Train GPT2-Small from hugging face pretrained checkpoint with intra-document masking and bos_override. Initialize bos_overrides to match current residual stream activations.

Training steps consists of 480 samples each with 1024 tokens, for 491_520 tokens per step. Samples come from open-webtext. The plots below show the log loss. I also plot the l2norm of the residual stream at each layer.

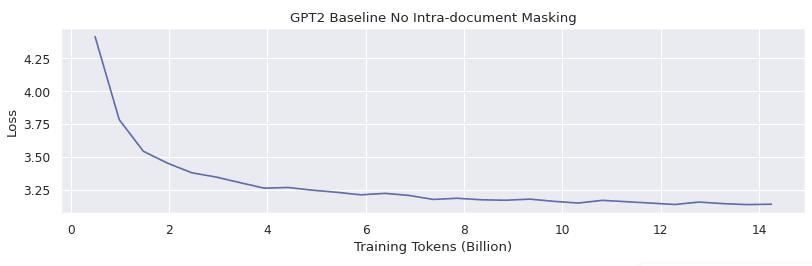
The plots below show the baseline GPT2 training behavior, indicating that the massive activations and large weight norms start to occur over the course of the first 10 billion training tokens.

The loss curves of all experiments that involve document masking, and datasets where position 0 always corresponds to a new sample, are plotted below. 

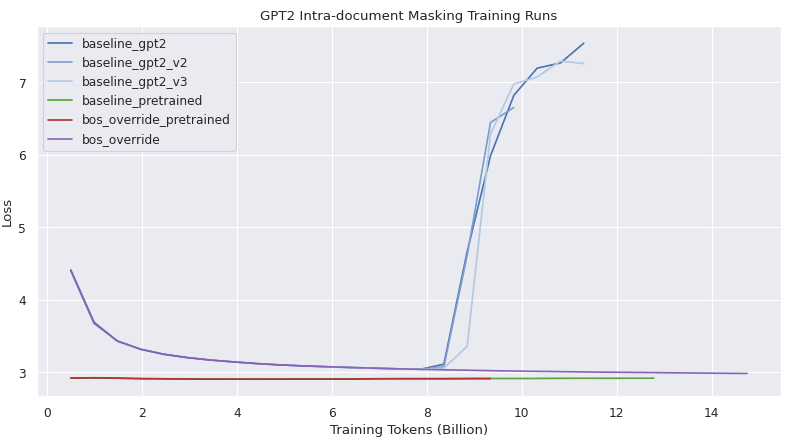
It is unclear to me why the baseline_gpt2 runs are diverging around 8 billion tokens. At this point I would assume an error in my implementation, though perhaps it is due to fragility in the learning rate, or an unlucky start. v2 and v3 of baseline_gpt were branched from a checkpoint of v1 around 6 billion tokens. The bos_override model is able to achieve a cross-entropy loss under 3 within 14 billion tokens (note this loss is defined against a dataset where each 1024 length sample is ensured to start with a fresh sequence).

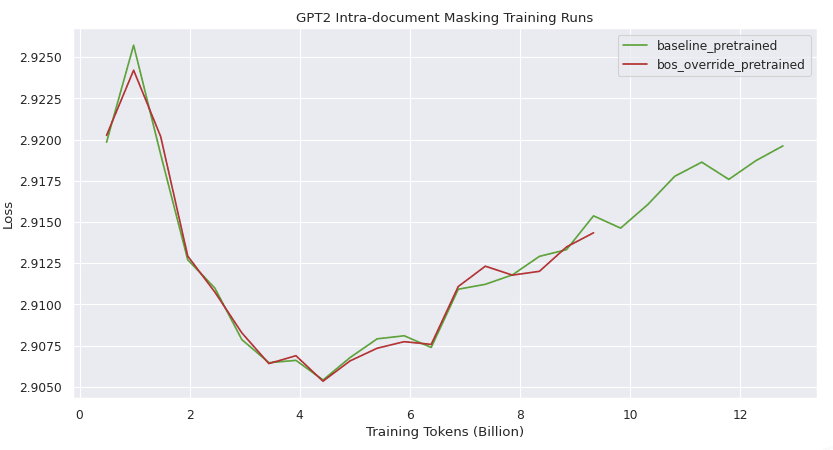
Zooming in to the 2 pretrained plots, they both exhibit similar overall loss behavior.

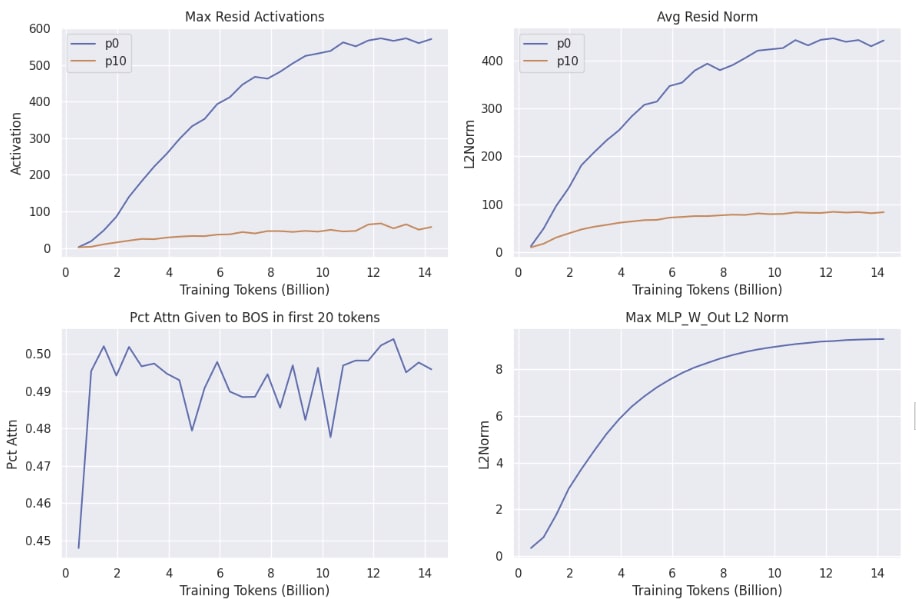
Next, the max activations in the residual stream are plotted for each training run.

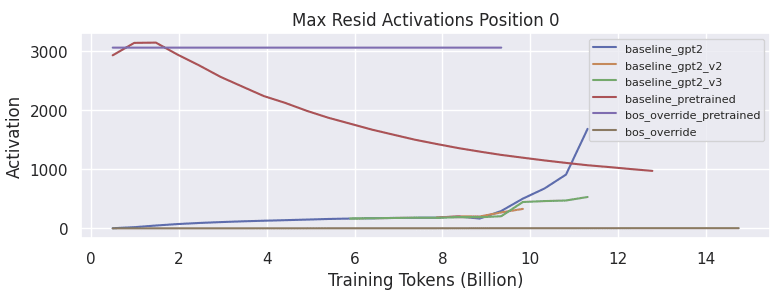
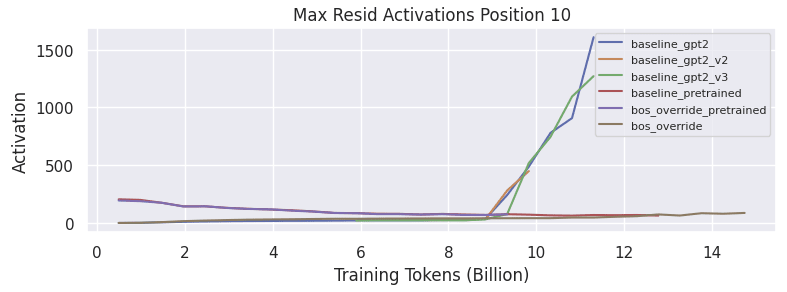
The bos_override models show extremely small change in the residual activation at position 0 over time. The gradient of a bias term initialized to 3,000 is likely incredibly small. The collapse of the baseline gpt2 training runs is correlated with a runaway spike in activation magnitude. It is unclear to me at this time why the baseline_pretrained model shows a decreasing max activation at position 0, from the initial 3000 down to 1000.

The attention plots are shown below. 

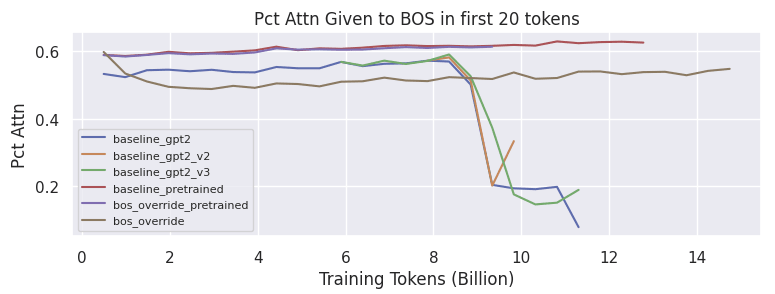
The collapse of the baseline gpt2 training runs is also correlated with attention to the bos token decaying. Interestingly, the bos_override model is still able to have substantial attention given to the bos_token, despite the magnitude of it in the residual stream staying near 0. 

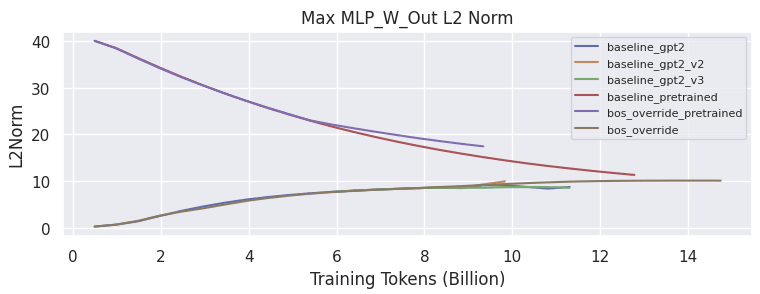
The max MLP_W_Out L2 norm appears to be converging around 10 for all models. 

Below are the final bos_override terms for the model trained from scratch. After applying normalization, these terms can still function similarly to massive activations, as the representation is sparse.

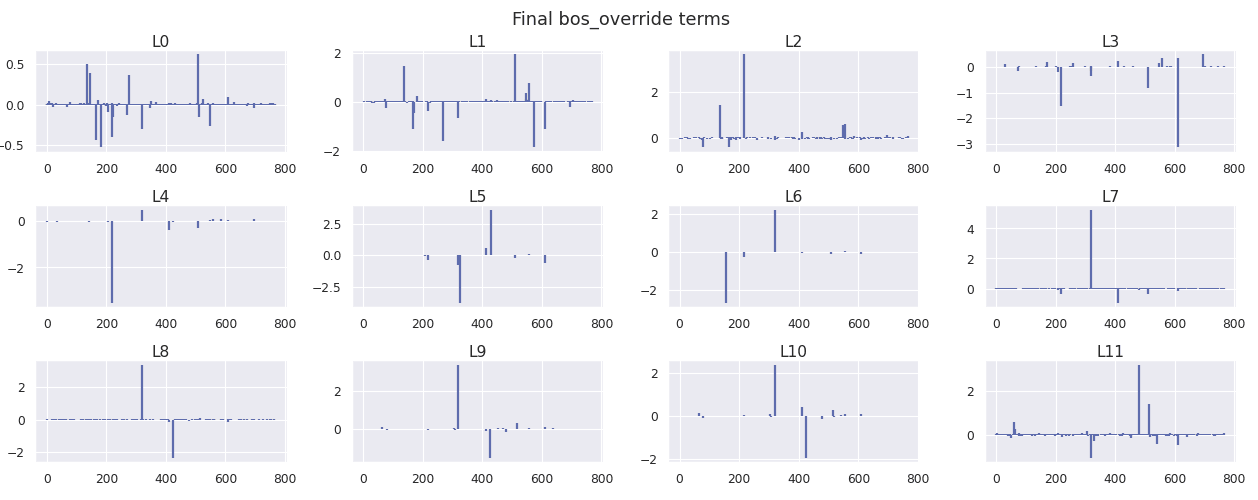
Notably, the residual stream for the bos_token is kept in the range -3 to 3. It is not obvious to me if this is preferred, but at a minimum it shows that massive activations are not a requirement for LLM performance or attention sink formation. To say whether or not this is an improvement, a valid next step may be to apply the changes to LLM speedrunning challenges such as https://github.com/KellerJordan/modded-nanogpt, to see if increased training stability from decoupling the attention sink from the MLP parameters enables faster learning rates.

 

1. ^{^}

   Efficient Streaming Language Models with Attention Sinks  https://arxiv.org/abs/2309.17453

2. ^{^}

   Massive Activations in Large Language Models https://arxiv.org/abs/2402.17762

3. ^{^}

   Why do LLMs attend to the first token? https://arxiv.org/abs/2504.02732

4. ^{^}

   Active-Dormant Attention Heads: Mechanistically Demystifying Extreme-Token Phenomena in LLMs https://arxiv.org/abs/2410.13835

5. ^{^}

   Round and Round We Go! What makes Rotary Positional Encodings useful? https://arxiv.org/abs/2410.06205

6. ^{^}

   Scaling a dimension in the residual stream before normalization shifts the mean of the residual stream away from zero, which has a knock off effect on every single dimension during any normalization steps that subtracts the mean. 

Discuss