本文探讨了随机变量冗余性的概念，特别是近似冗余。文章定义了变量Γ在X1和X2上冗余的条件，并引入了近似冗余的概念，通过图表和公式描述了近似冗余的数学表达。核心问题是寻找一个最大冗余变量Ω，它包含任何其他近似冗余变量中关于X的所有信息，并且是X的一个近似确定性函数。文章提出了一项悬赏，寻求证明这种最大冗余变量Ω的存在性，并给出了精确情况下的直观解释。解决这个问题将对电话定理的新版本以及自然潜在变量的计算产生重要影响。

💡**冗余变量定义**: 变量Γ在两个随机变量X1和X2上冗余，当X1和X2各自包含关于Γ的全部信息，即P[Γ|X1]=P[Γ|X2]=P[Γ|X]。

🧮**近似冗余的数学表达**: 通过KL散度定义近似冗余，公式为ϵred≥DKL(P[X,Γ]||P[X1]P[X2|X1]P[Γ|X2])和ϵred≥DKL(P[X,Γ]||P[X2]P[X1|X2]P[Γ|X1])。

🎯**最大冗余变量Ω**: 目标是找到一个最大冗余变量Ω，它包含任何其他近似冗余变量中关于X的所有信息，且Ω是X的一个近似确定性函数，满足ϵdet≥H(Ω|X)。

💰**悬赏内容**: 悬赏$500寻求证明对于任意两个随机变量X1和X2，都存在满足上述要求的Ω，且误差界限合理（ϵ与其他ϵ按ϵ²比例缩放）。

⚙️**精确情况下的直观解释**: 在精确情况下，可以通过构建二分图，将X1和X2的值作为顶点，如果P[X1=x1,X2=x2]>0则连接顶点。最大冗余变量f(X)可以定义为X所在的连通分量。

Published on May 6, 2025 11:05 PM GMT

A lot of our work involves "redunds". A random variable $\Gamma$ is a(n exact) redund over two random variables $X_1,X_2$ exactly when both

$X_1\to X_2\to \Gamma$

$X_2\to X_1\to \Gamma$

Conceptually, these two diagrams say that $X_1$ gives exactly the same information about $\Gamma$ as all of $X$, and $X_2$ gives exactly the same information about $\Gamma$ as all of $X$; whatever information $X$ contains about $\Gamma$ is redundantly represented in $X_1$ and $X_2$. Unpacking the diagrammatic notation and simplifying a little, the diagrams say $P\left[\Gamma |X_1\right]=P\left[\Gamma |X_2\right]=P\left[\Gamma |X\right]$ for all $X$ such that $P\left[X\right]>0$.

The exact redundancy conditions are too restrictive to be of much practical relevance, but we are more interested in approximate redunds. Approximate redunds are defined by approximate versions of the same two diagrams:

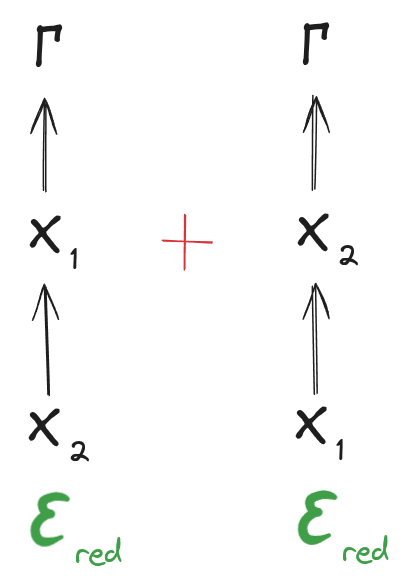
Unpacking the diagrammatic notation, these two diagrams say

${ϵ}_{red}\ge D_{KL}\left(P\right[X,\Gamma \left]||P\right[X_1\left]P\right[X_2|X_1\left]P\right[\Gamma |X_2\left]\right)$

${ϵ}_{red}\ge D_{KL}\left(P\right[X,\Gamma \left]||P\right[X_2\left]P\right[X_1|X_2\left]P\right[\Gamma |X_1\left]\right)$

This bounty problem is about the existence of a(n approximate) maximal redund $\Omega$: a redund which contains (approximately) all the information about $X$ contained in any other (approximate) redund. Diagrammatically, a maximal redund $\Omega$ satisfies:

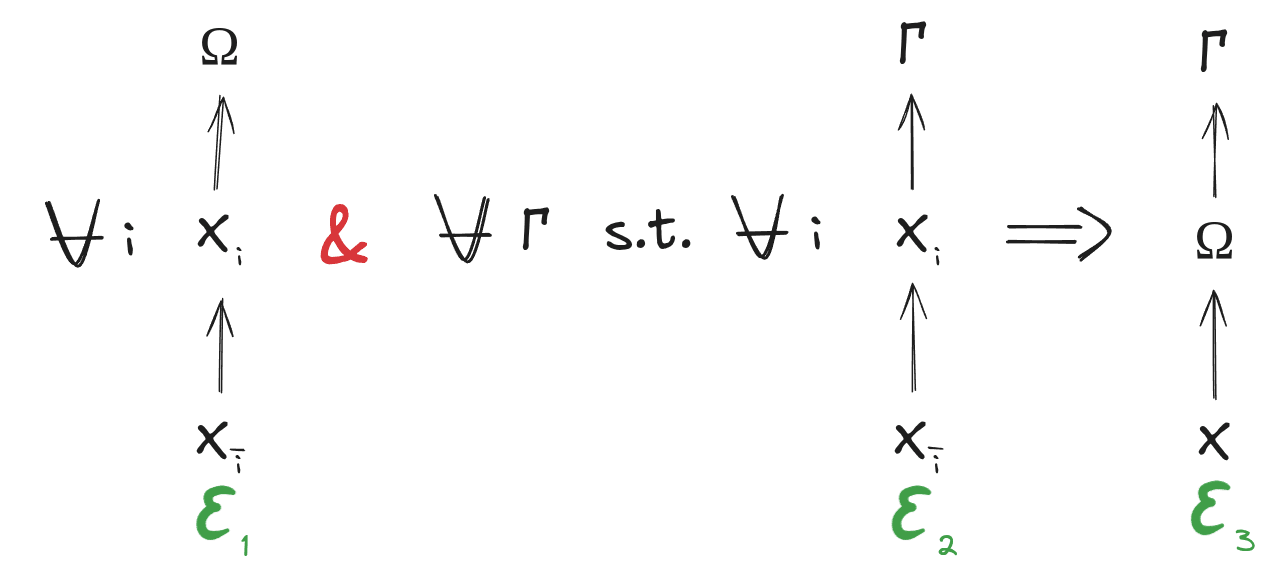
Finally, we'd like our maximal redund $\Omega$ to be an approximately deterministic function of $X$, i.e. ${ϵ}_{det}\ge H\left(\Omega |X\right)$, which is equivalent to the diagram

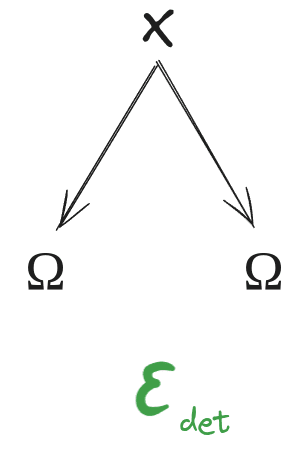
What We Want For The Bounty

This bounty pays out $500 for establishing that there always, over any two random variables $X_1$, $X_2$, exists an $\Omega$ satisfying the requirements above, i.e.

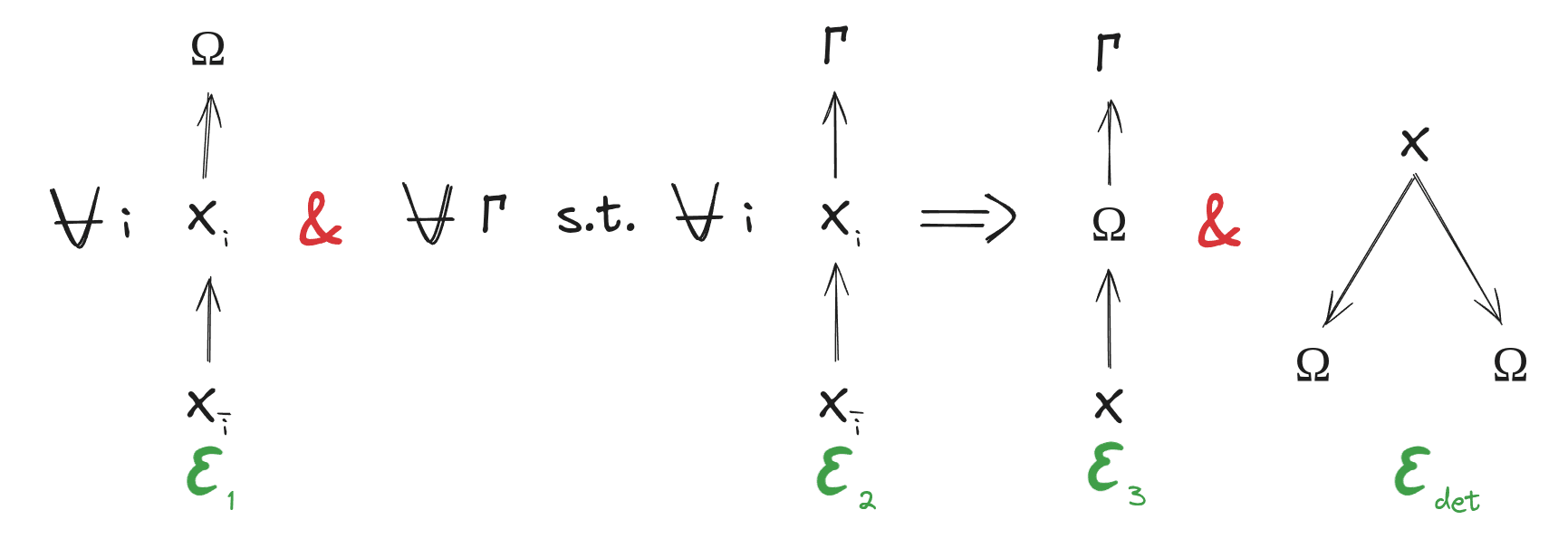
... with reasonable error bounds.

What counts as reasonable error bounds? We're expecting all the other $ϵ$'s to scale with ${ϵ}_2$ in the diagrams above, and ideally be small constant multiples of ${ϵ}_2$. In other words: the higher the approximation error on allowable redunds $\Gamma$, the more approximation error we allow for all the conditions on $\Omega$. Reasonableness of error bound is partially a judgement call on our part, but small constant (like e.g. 2 or 3) multiples of ${ϵ}_2$ would definitely suffice.

Bounds should be global, i.e. apply even when ${ϵ}_2$ is large. We're not interested in e.g. first or second order approximations for small ${ϵ}_2$ unless they provably apply globally.

If the error bounds are sufficiently reasonable, a solution to this problem will also solve our other open bounty problem, paying out another $500, for a total of $1000.

If people post major intermediate steps which are load-bearing for an eventual solution, we might allocate the bounty based on our judgement of different peoples' relative contributions; the hope is to incentivize sharing intermediate results.

We might also partially pay out for counterexamples. That's a judgement call depending on how thoroughly the counterexample kills hope of any theorem vaguely along the lines intended.

In terms of rigor and allowable assumptions, roughly the level of rigor and assumptions in the posts linked above is fine.

Some Intuition From The Exact Case

A proof in the exact case is straightforward; we'll walk through it here to build some intuition.

The exact redundancy conditions say

$P\left[\Gamma |X\right]=P\left[\Gamma |X_1\right]=P\left[\Gamma |X_2\right]$

wherever $P\left[X\right]>0$. So, we can form a bipartite graph, where each vertex represents a value $x_1$ of $X_1$ or a value $x_2$ of $X_2$, and two vertices are connected iff $P[X_1=x_1,X_2=x_2]>0$. Then the definition of redundancy  says that, for ANY redund $\Gamma$, $P\left[\Gamma |X_1\right]$ and $P\left[\Gamma |X_2\right]$ are the same for ANY values of $X_1$ and $X_2$ (respectively) in the same connected component.

So, let $f\left(X\right)$ be defined as the connected component in which $X$ falls. For any redund $\Gamma$, $P\left[\Gamma |X\right]$ must be a function of $f\left(X\right)$ (since two $X$-values in the same connected component have the same $P\left[\Gamma |X\right]$). Thus

$X\to f\left(X\right)\to \Gamma$

$f\left(X\right)$ is therefore a(n exactly) deterministic function of $X$, and (exactly) mediates between X and any redund $\Gamma$. Thus, $f\left(X\right)$ satisfies our requirements, in the exact case (i.e. when ${ϵ}_2=0$).

Alas, this proof does not easily generalize to the approximate case.

Why We Want This

This is a conjecture which we've had on the back burner for a while, and it would be relevant in many places. It would solve our other open bounty problem, it would likely be our starting point for a new version of the Telephone Theorem which more explicitly connects to the natural latents framework, and it would directly simplify the problem of computing natural latents numerically. Probably there are other use-cases which we're not thinking about right at the moment.

Discuss