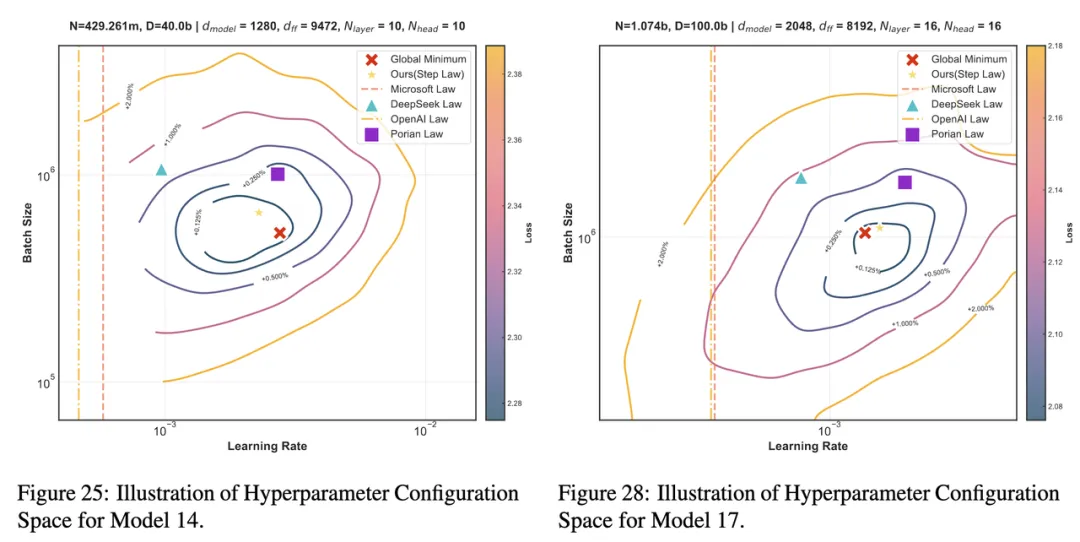图一：在 400M 的 Dense LLM 上训练 40B Token（左）和在 1B 的 Dense LLM 上训练100B Token（右）的超参-损失等高线图

我们对行业内不同方法进行了比较，所有方法都转换成了预测  Optimal Token Wise BatchSize。这里所有的等高线都是从头训练的小模型所得的真实收敛后的 Train Smooth  Loss。左右两张图的所有等高线，分别来自于两组共 240 个采用不同超参（Grid Search）的端到端训练的小模型。Global  Mimimum 是来 120 个小模型中最终 Train Smooth Loss 最小的那个。等高线表示距离 Global Mimimum  的从最终 loss 角度的相对距离。而超越 +2% 的点位，并没有体现在图中。

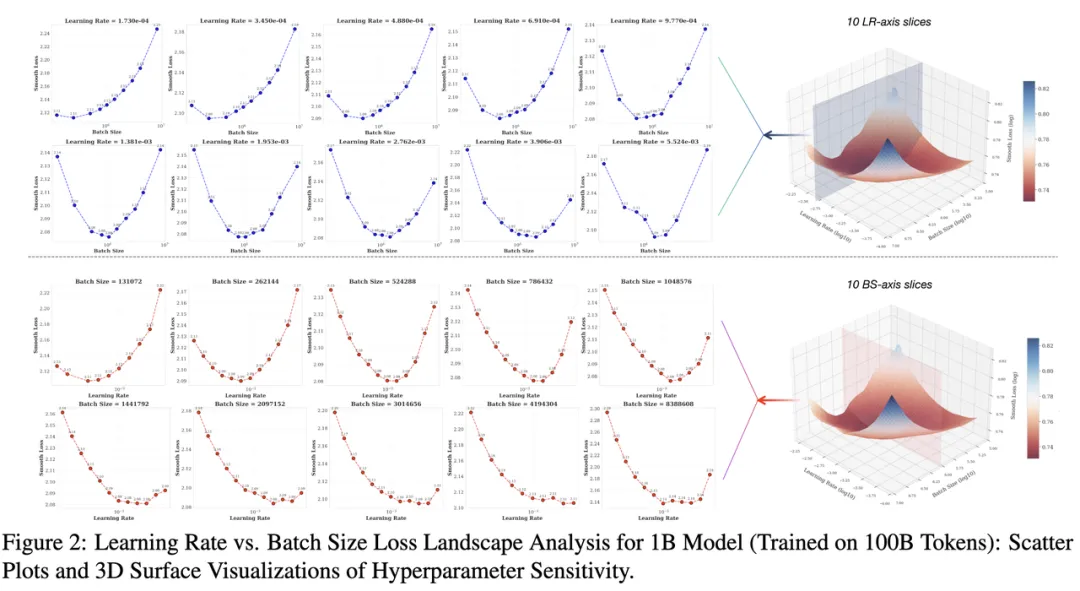
图二：Learning Rate 与 Batch Size 在 1B 模型训练 100B Token 上的损失分布。散点图（左）与 3D 曲面（右）图中的每一个实心点都是真实值，是 120 个从头训练的一个小模型，在训练结束之后的收敛 Loss

为了展示这样的凸性，研究员们构造了如右图一样的  3 维空间，空间的横轴为 Learning Rate，纵轴为 Batch-size，高度轴为  Loss。对于这个三维空间我们进行横面和竖面的切割。

如左上图得到固定不同的 Learning Rate 情况下，最终收敛的 Train  Smoothed Loss随着 Batchsize 的变化。而左下图是固定不同的 Batchsize 情况下，最终收敛的 Train  Smoothed Loss 随着 Learning Rate 的变化。可以显著的观测到一种凸性，且在凸性的底端，是一个相对平坦的区域。这意味着  Optimal Learning Rate 和 Batchsize 很可能是一个比较大区域。

为了便于学界和业界应用，我们推出了一款通用的最优超参数估算工具——（https://step-law.github.io），其预测结果与穷举搜索的全局最优超参数相比，性能仅有 0.09% 的差距。同时，我们还在该网站上公开了所有超参数组合的 loss 热力图，以进一步推动相关研究。

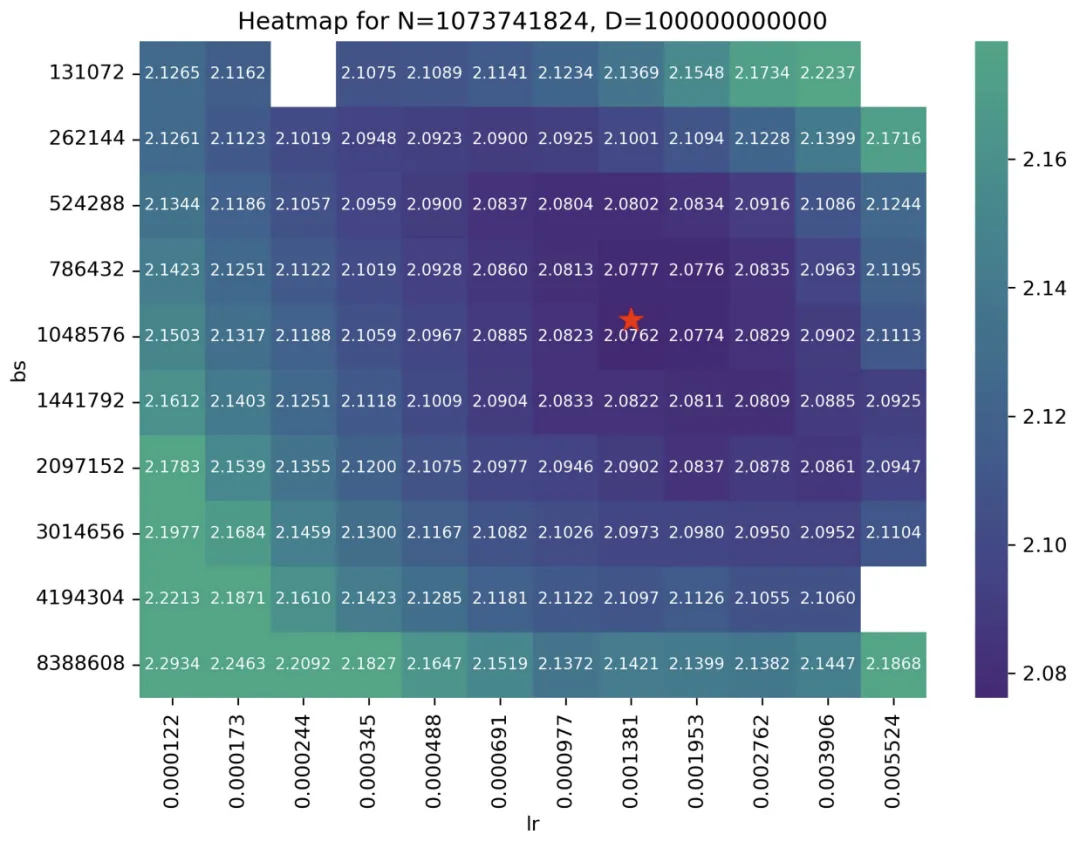
图三：1B 模型、100B Token 训练上的 LR 与 BS 热力图

在这张图中，每一个点上的数字都是从头训练的一个小模型（共训练了 120 个小模型），在训练结束之后的收敛真实 Train Smoothed Loss。红点是上述公式的预估值所对应的 BS、LR 位置。其中空白的部分，是因为种种原因训练失败的点位。

所有热力图见：https://step-law.github.io/

「相关研究梳理】如何为大规模训练找到最优超参？

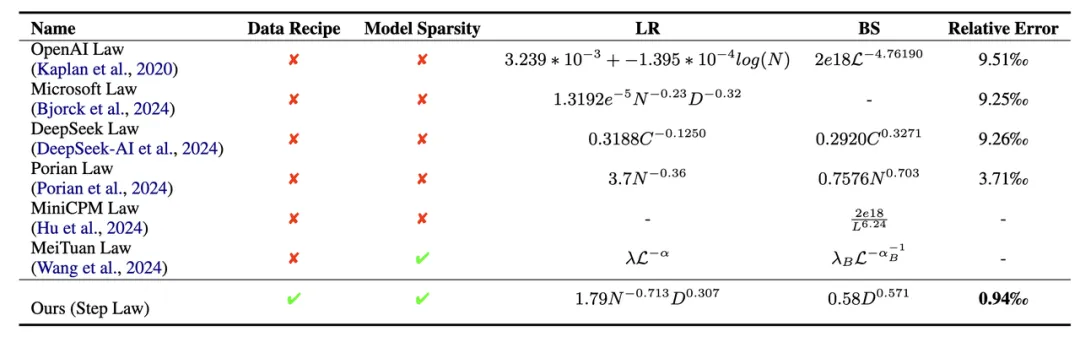表一：不同方法的最佳超参数缩放定律比较，其中 Data Recipe 是指是否有在不同的预训练语料的配比下的最优超参进行研究

Model  Sparsity 是指是否同时支持 MoE Model 和Dense Model，以及不同的稀疏度下的 MoE 模型。LR 指的是  learning Schedule 中的峰值 Learning Rate，其中 BS 值得是 Token Wise 的 Batch Size。

「普适性」超参数缩放法则的三大性质

1. 跨模型形状的稳定性

我们还深入探讨了不同模型形状（如宽度与深度的不同组合）对缩放规律的影响，发现无论模型是以宽度为主还是深度为主，抑或是宽深平衡的设计，Step  Law  均表现出了高度的稳定性。这表明，缩放规律不仅适用于特定类型的模型结构，在更广泛的架构设计空间中依然适用，为复杂模型架构的设计和优化提供了指导意义。实验结果如下图所示：

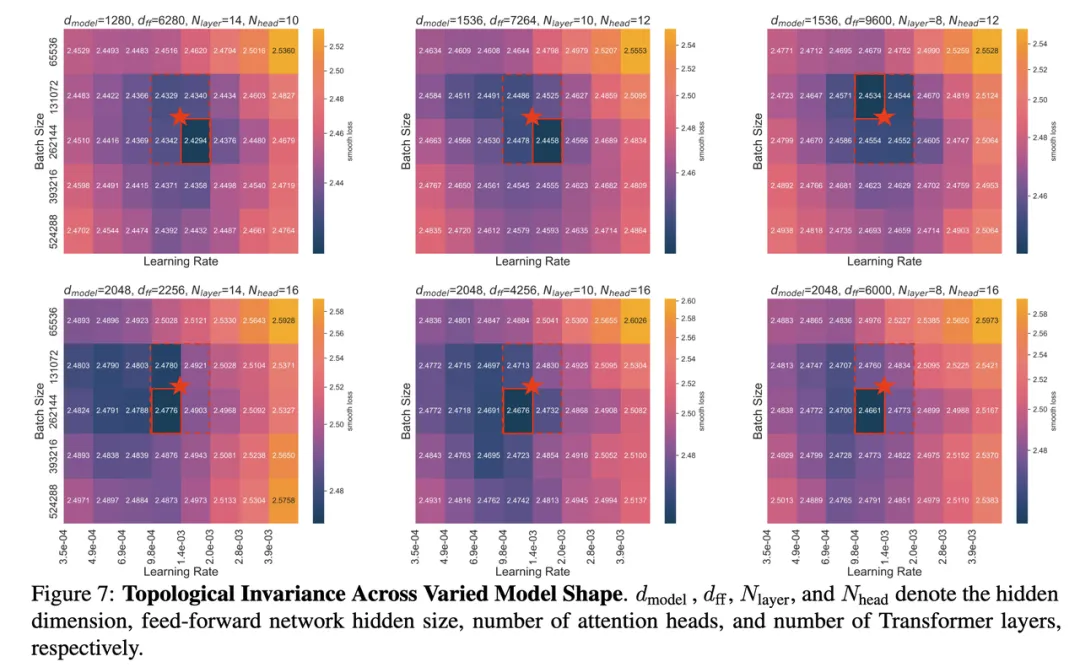
图四：最优超参在不同 Model Shape 下的拓扑不变性。这里固定了模型的非词表参数量的大小和模型的训练 Token 数

在这里，研究团队虽然固定了上面的两项，但使用了不同的  Model Shape。例如变换了层数，从左到右分别是 14/10/8 层；变换了 Model Hidden Dimension，分别包括  1280/1536/2048 这三种；同时变换了 6 种不同的 FFN 倍数(FFN_media_dim/model_dim)，从 1.1 倍 ~  6.25 倍。

其中红色五角星的点是 Step Law 预测的点位，可以观察到 Step_law 在 6 个不同的Shape上都预测到了  Global Minimum 附近。然而也可以同时观察到，不同的 Model Shape，Bottom 的一片区域的位置是会发生 shift  的。

2. 跨模型架构的泛化性

我们的研究结果发现，这一缩放规律不仅适用于稠密模型，还能很好地推广到不同稀疏度的 MoE (Mixture-of-Experts) 模型，对于不同的模型结构展示了极强的泛化能力。实验结果如下图所示：

研究员们在不同稀疏度，不同  D/N 的 MoE 模型配置，每一种配置都从头训练了 45 个小模型，来做最优超参搜取。共计从头训练了 495 个不同稀疏度、不同超参、不同  D/N 的 MoE 模型。从而得到了不同配置下的基于真实值的 Global Minimum Train Smoothed Loss。其中除了一组  D/N = 1 的实验，其余实验 Step Law 预测位置都在 Global Minimum+0.5%的范围之内。并且大多数配置下都在  Global Minimum+0.25% 的范围之内。充分的验证了 Step Law 的鲁棒性。详细结果可以参考论文的附录部分。

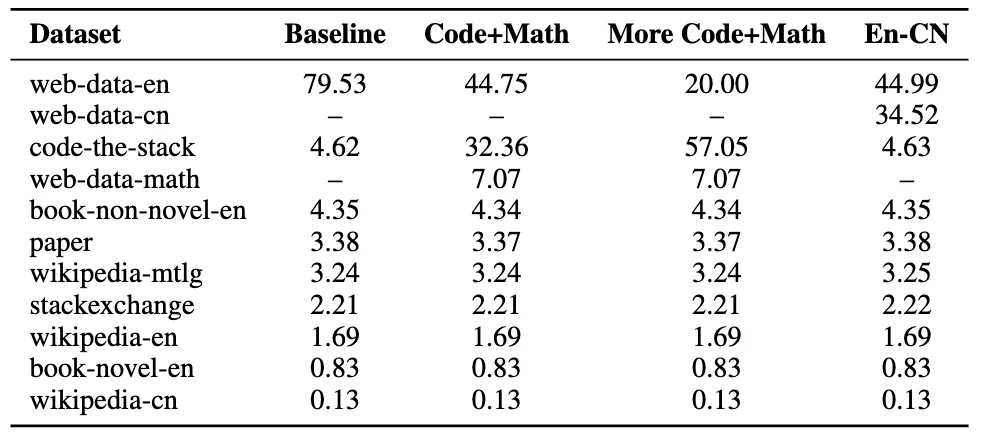
表二：实验的不同数据分布

其中  Baseline 是得出 Step Law 的训练 Recipe。而 Code-Math，是压缩英文 web-data 的配比近一半，扩大  code-math 的比例至近 40%。而 More Code-Math 比例更加极端，将英文 web-data 的配比压缩为之前的 1/4，将  Code-math 扩大为近 2/3。EN-CN 是下调英文 web-data 的配比近一半，将余量的部分都转化为中文网页数据。

实验结果如下图所示：

每一个图都是从头训练了  45 个模型，每一个模型除了 Bs/lr 不同以外，其他设置完全相同。总共训练了 135 个在三种数据分布下的模型。其中 Global  Minimum 是通过这种 grid search 的方法得到的最低 Final Train Smoothed Loss 的真实值。Step  Law 预测出来的最优 Batch Size/Learning Rate 都在最低 Loss +0.125%/0.25% 的范围内。

我们通过对比分析发现，学习率调度策略对最优超参选择会产生显著影响。如下图所示，我们揭示了传统学习率衰减与固定最小学习率方案间的重要差异：

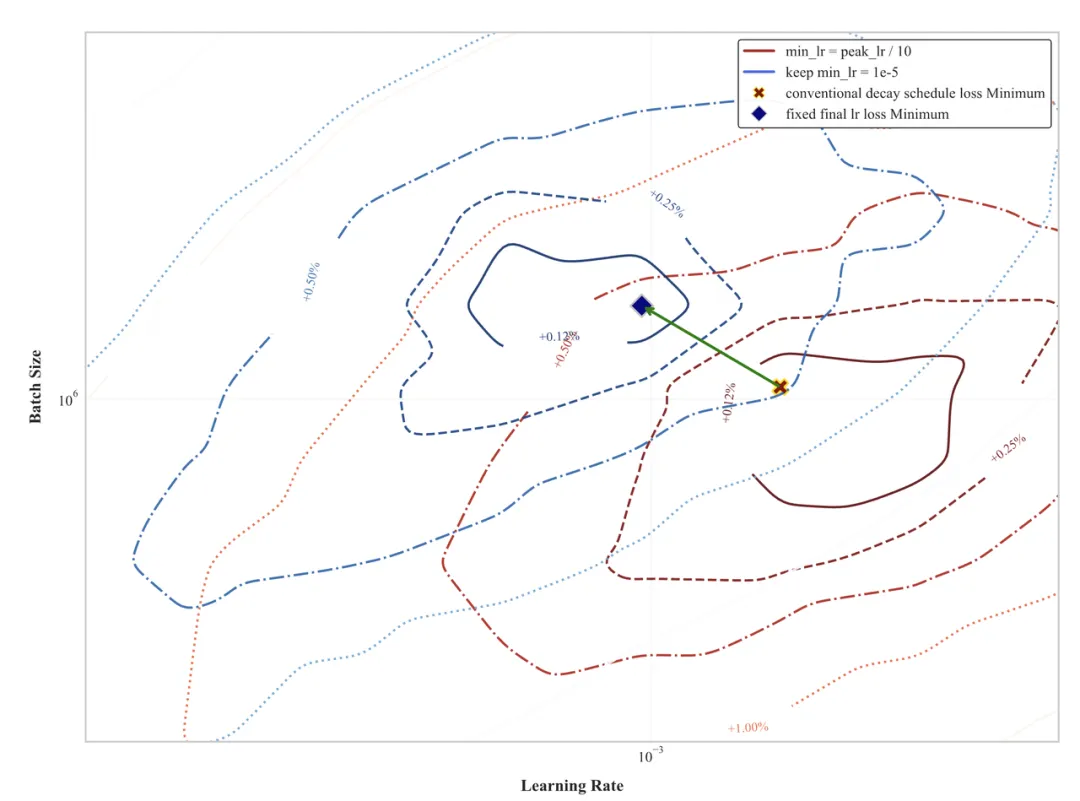
图七：不同学习率策略的比较

蓝色等高线  (传统衰减策略): 学习率会从一个最大值 (max_lr) 逐渐减小到一个最小值 (min_lr，常是峰值的十分之一)。红色等高线  (固定最终学习率策略): 保持一个固定的最小学习率 (min_lr = 1e-5)，而不是像传统方法那样与最大学习率挂钩。

两张图都分别为  120 个从头训练的模型，在相同的 batch size/learning rate 范围内做的 Grid Search。红色和蓝线的  Global Minimum 都是各自配置下的真值-最小的 Final Train Smoothed Loss。可以观察到改成  max_lr/10 之后，蓝点会向左上方偏移，即更小的 Learning Rate 和更大的  Batchsize。如果不是对比相对值，而是对比真值，min_lr=1e-5 的最终收敛 loss 普遍小于 max_lr/10。

相关的真值开源在 https://github.com/step-law/steplaw

退火机制：随着训练的进行，学习率通常会逐渐降低（即“退火”），以便在训练后期进行更精细的参数更新。然而，这种调度通常是耦合的，即高初始学习率也提高了最低学习率的阈值。

2. 训练损失与验证损失的最优超参一致性

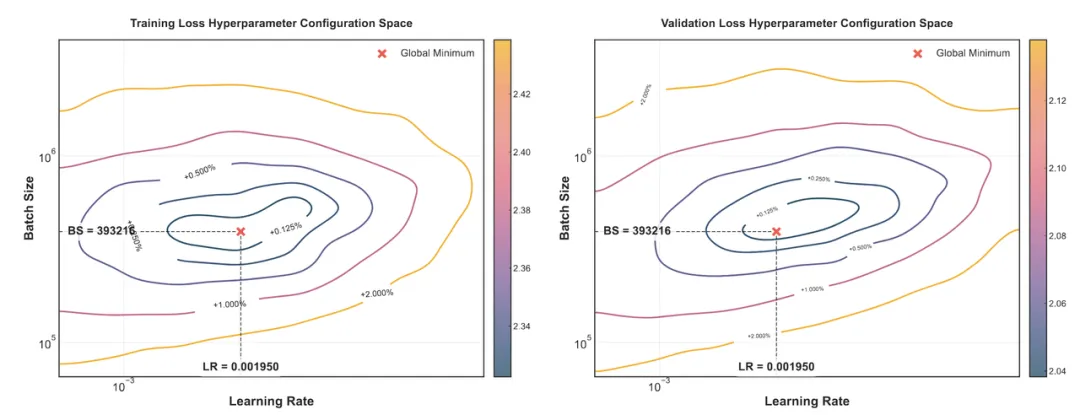
两张图都是在同一组实验下进行，对于相同的模型尺寸，相同的训练 Token 数，分别采用了 64 组不同的超参进行 Grid Search。从而得到64个模型的 Final Train Smoothed Loss、和Validation Loss。

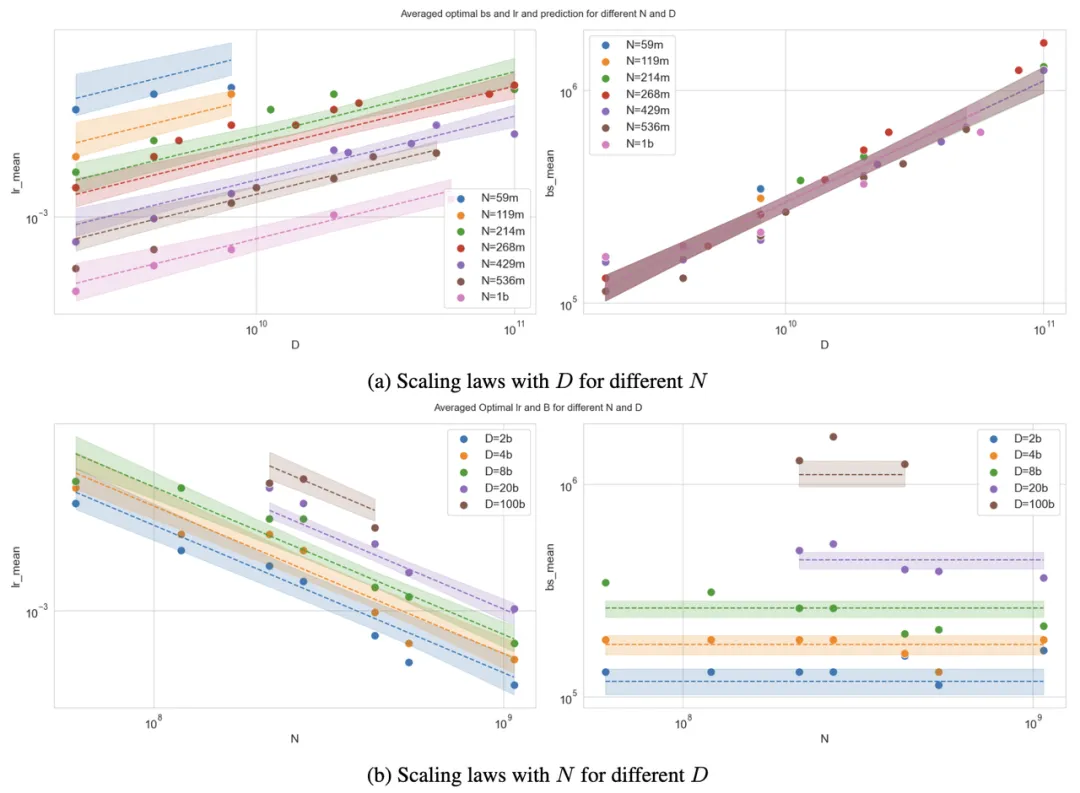
曲线表示超参数缩放定律的预测结果，阴影区域表示基于采样拟合策略得到参数不确定性范围。图上的每一个点，背后都代表着  45~120 个采用了不同的超参的从头训练的模型。图上的每一个点位都在不同的 Model Size、Data Size 下通过 Grid  Search 得到的最优的超参 (Optimal Learning Rate，Optimal Batch Size)。这张图总共涉及了 1912  个从头训练的 LLM。

真值和拟合方法开源在 https://github.com/step-law/steplaw。

最优学习率：随模型规模增大而减小，随数据规模增大而增大。

最优批量大小：随数据规模增大而增大，与模型规模弱相关。

讨论与未来工作

在给定模型、训练 Token 数的情况下，(Loss , bs, lr) 这三维空间是否是真正的凸性。
是否有更好的 optimal BS LR 的拟合方法，并且可以兼容 BS、LR 的内在关系。
尽管 Step Law 在不同 Model Shape、不同稀疏的 MoE 模型是鲁棒的，但是次优的区域是在不同配置下是变化的，有无更好的解释方法。
上文中这些基于海量 Grid Search 的数据驱动的结论的理论解释。
不同的超参、不同 Model Size、Model Shape、Model Sparsity 下的 Training Dynamic 研究。

如果你有与开源 AI、Hugging Face 相关的技术和实践分享内容，以及最新的开源 AI 项目发布，希望通过我们分享给更多 AI 从业者和开发者们，请通过下面的链接投稿与我们取得联系:

https://hf.link/tougao