‍

现代机器学习问题通常涉及兼顾多个目标，有时这些目标相互冲突。想象一下训练一辆自动驾驶汽车：你希望它安全高效地行驶，在某些情况下可能需要不同的转向调整。传统的优化方法，如梯度下降，主要针对单一目标而设计。Quinton 和 Rey 最近发表了一篇题为“多目标优化的雅可比下降法”的研究论文，介绍了一种新颖且有原则的方法来解决这些多目标场景。

Jacobian Descent For Multi-Objective Optimization

https://arxiv.org/html/2406.16232v1

https://github.com/TorchJD/torchjd

这篇论文可在 arXiv ( arXiv:2406.16232v2 ) 上找到，它提出了一种梯度下降的直接推广方法，称为雅可比下降法 (Jacobian Descent, JD)。雅可比下降法不依赖单一梯度来指导优化，而是利用雅可比矩阵，这是一个强大的工具，将所有单个目标的梯度组合成一个结构。

从单梯度（Gradient）到雅可比矩阵

首先我们来了解一下核心思想。在单目标优化中，我们有一个想要最小化的损失函数。梯度下降通过沿梯度的反方向移动来迭代更新模型的参数。

与多目标优化的关键区别在于，我们有一个目标函数向量，例如 f(x) = [f₁(x), f₂(x), …, fₘ(x)]ᵀ，其中每个 fᵢ(x) 代表一个不同的目标。雅可比矩阵，用 Jf(x) 表示，是一个矩阵，其中每一行都是单个目标的梯度：

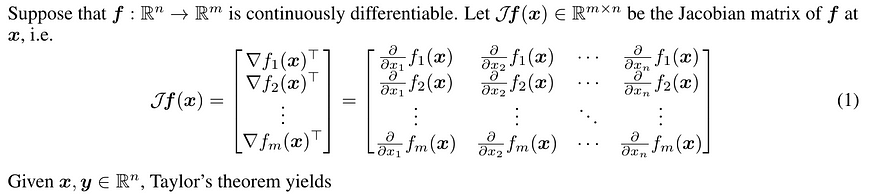
其中x表示模型的参数，n是参数的数量。

当我们有多个目标时，我们就有多个“山峰”，每个山峰都有自己的梯度。雅可比矩阵将所有这些单独的梯度收集到一个矩阵中。雅可比矩阵的每一行对应于一个目标函数的梯度。

聚合器（Aggregator）的作用

雅可比下降法的核心创新在于如何使用这个雅可比矩阵来更新参数。论文中引入了聚合器的概念，用 A 表示。这个聚合器是一个函数，它以雅可比矩阵为输入，输出一个向量，该向量指示参数更新方向：

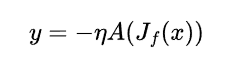
其中，η 为学习率，y 为参数更新。不同的聚合器会导致不同的多目标优化算法。本质上，现有的多目标优化方法可以看作是具有特定聚合器的 JD 的特例。

由于我们有多个梯度（每个目标一个），我们需要一种方法将它们组合成一个更新方向。聚合器是“厨师”，它采用这些单独的梯度（配料）并创建一个组合的“菜肴”（更新方向）。不同的聚合器使用不同的“配方”来组合梯度，从而产生不同的优化算法。

应对目标冲突的挑战

多目标优化的一个主要障碍是处理相互冲突的目标。想象一下，一个目标将参数推向一个方向，而另一个目标则推向相反的方向。许多现有方法在这种情况下都难以应对。本文强调，他们提出的使用特定聚合器的方法旨在解决此问题。

AuPGrad：一个不冲突的聚合器

双锥（Dual Cone）（理解 AuPGrad 的关键）：这是数学变得有点抽象的地方，但直觉是可以控制的。想象一组向量（我们目标的梯度）。双锥表示所有不与这些向量“冲突”的方向。更正式地说，如果一个向量与原始集合中的每个向量的点积都是非负的，则该向量位于双锥中。

直觉：将双锥视为更新的“安全区”。在双锥内朝任何方向移动都可以保证我们不会使任何单个目标变得更糟（至少在局部）。这对于处理冲突的目标至关重要。

为了解决现有聚合器的局限性，作者引入了AuPGrad，即“梯度无冲突投影（unconflicting projection of gradients）”聚合器。AuPGrad 背后的关键思想是将每个单独的梯度投影到其他梯度的对偶锥上。这种投影确保更新方向不会增加任何目标函数，从而有效地解决冲突，同时保留单个梯度的影响。

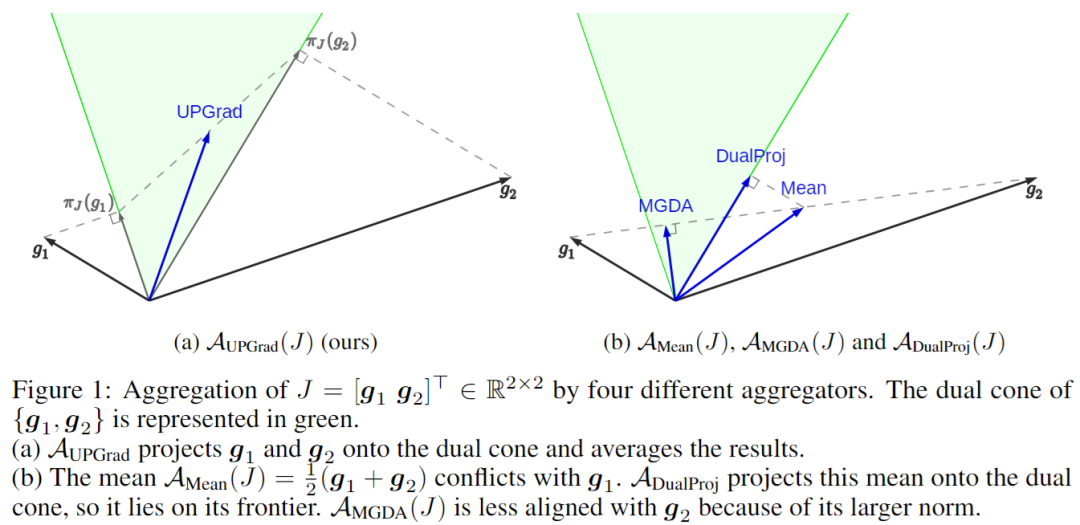
从数学上讲，向量 x 在 J 的行对偶锥上的投影定义为：

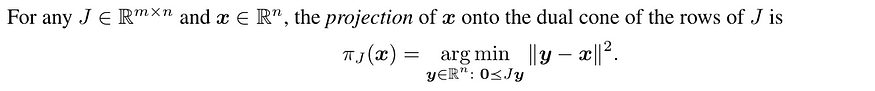
然后，AuPGrad 被定义为这些预测的平均值：

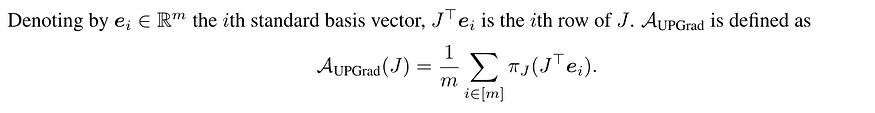
更强的收敛保证

帕累托最优（Pareto Optimality）：在多目标优化中，没有单一的“最佳”解决方案。相反，我们有一组称为帕累托前沿的最优权衡。如果您无法在不损害至少一个其他目标的情况下改善一个目标，则解决方案是帕累托最优的。

本文的一项重要贡献是对使用 AuPGrad 的 JD 进行理论分析。作者证明了与现有方法相比更强的收敛保证，表明在某些条件下（平滑和凸目标），使用 AuPGrad 的 JD 收敛到帕累托前沿。帕累托前沿表示一组最优解，其中一个目标的改善不可避免地会恶化至少一个其他目标。

迈向高效实施：格莱姆（Gramian）方法

JD 的一个潜在瓶颈是计算和存储可能很大的雅可比矩阵。为了解决这个问题，本文概述了一种使用Gramian 矩阵的有效实现策略，定义为 Gf(x) = Jf(x) Jf(x)ᵀ。

格拉姆矩阵：格拉姆矩阵是一种表示不同梯度之间的关系（包括冲突）的方法，无需存储完整的雅可比矩阵。它就像是目标之间相互作用的总结。这可以使计算更有效率，尤其是在处理大量目标时。

Gramian 捕获所有梯度对之间的内积，无需明确计算完整的雅可比矩阵即可提供有价值的信息。作者展示了加权聚合器（包括 AuPGrad）的情况。这允许更节省内存的实现，尤其是当目标数量远大于参数数量时。

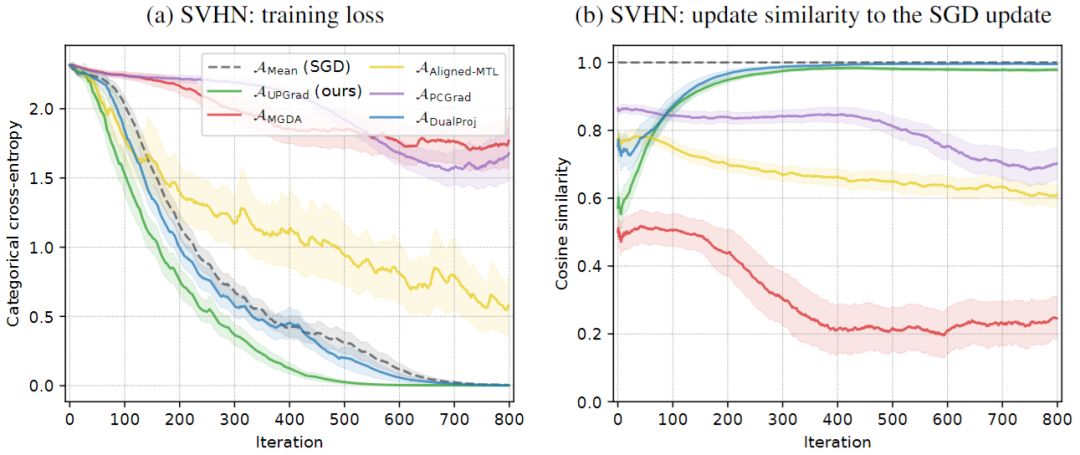
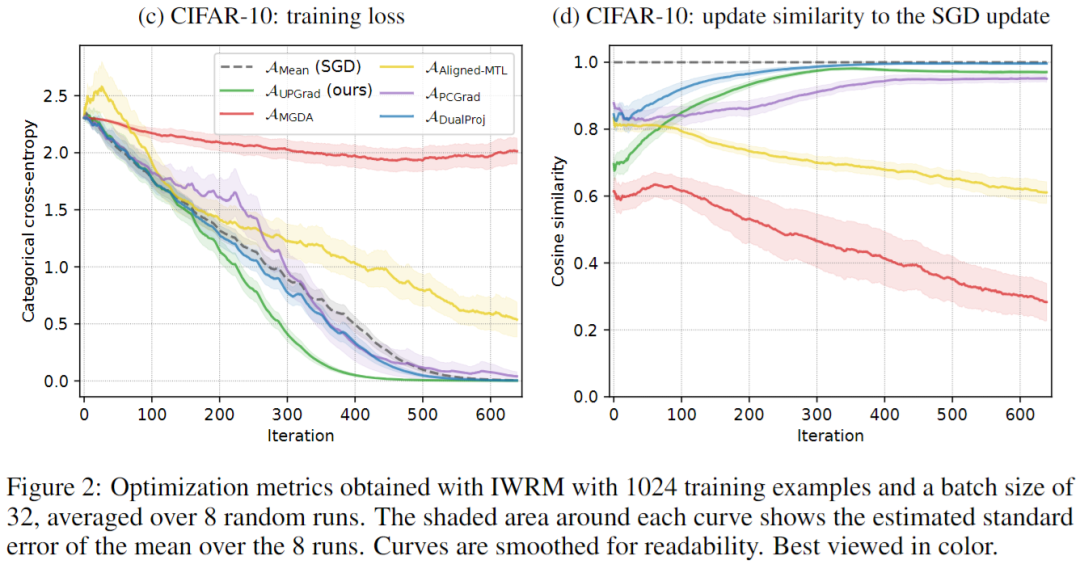
结论和未来方向

“雅可比下降法在多目标优化中的应用”论文通过引入一个原则性强且理论合理的多目标优化框架，为该领域做出了重大贡献。JD 凭借其灵活的聚合器设计，统一了现有方法，并提供了解决目标冲突的复杂问题的强大工具。所提出的 AuPGrad 聚合器因其解决冲突的能力和强大的收敛保证而脱颖而出。

这项研究为未来多目标优化的进步奠定了坚实的基础，并鼓励在各种机器学习领域更广泛地采用这些强大的技术。附带的 PyTorch 库进一步促进了雅可比下降法的探索和应用。

TorchJD 是一个扩展 autograd 的库，可通过 PyTorch 实现雅可比下降法。它可用于训练具有多个目标的神经网络。特别是，它支持多任务学习，具有文献中各种各样的聚合器。它还支持实例风险最小化范式。完整文档可在torchjd.org上找到，其中包含几个使用示例。

使用 TorchJD 的主要方法是根据用例，用 torchjd.backward 或 torchjd.mtl_backward 调用替换通常的 loss.backward() 调用。

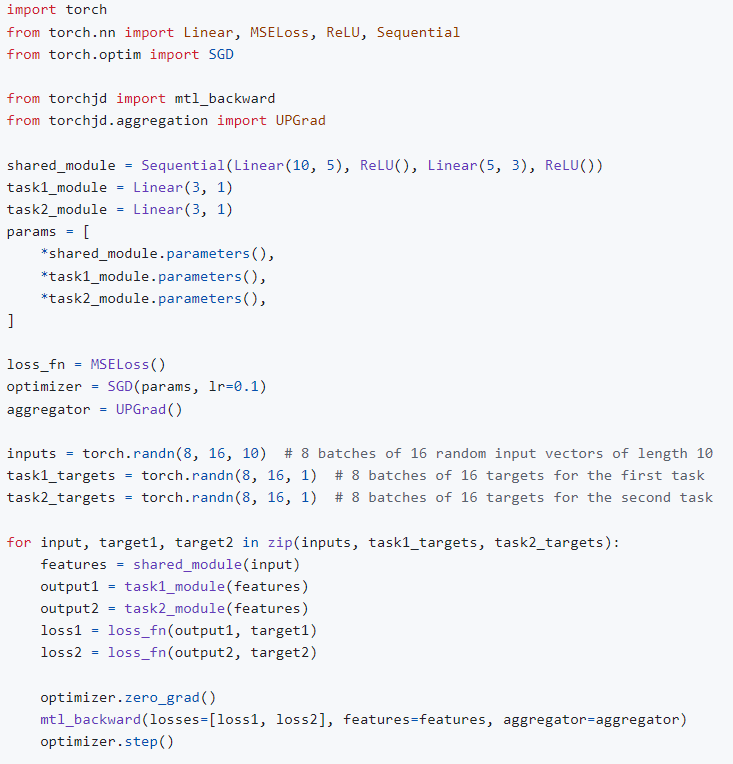
以下示例展示了如何使用 TorchJD 训练具有雅可比下降法的多任务模型（使用 UPGrad）。