index_new5.html
../../../zaker_core/zaker_tpl_static/wap/tpl_guoji1.html
![]()
该研究通过构建流体网络,将流体涡旋的相互作用视为节点和边,揭示了流体运动隐藏的空间和拓扑特性。研究发现,流体中涡旋的空间分布具有自相似性,且自相似性指数受动能和涡度衰减速率影响。高湍流性条件下,自相似性更显著,而低湍流性时则逐渐消失。此外,研究还通过重整化群变换,发现涡旋网络的尺度不变性在高湍流性条件下更强。研究还定义了“控制标度”,发现控制代价随时间呈幂律衰减,但在高湍流性条件下衰减不明显。这项研究为理解复杂流体系统提供了新视角,并为流体控制和优化设计提供了理论依据。
🌀 将流体涡旋间的相互作用视为网络,每个涡旋是节点,相互作用是边,构建流体网络,揭示流体运动的隐藏结构。
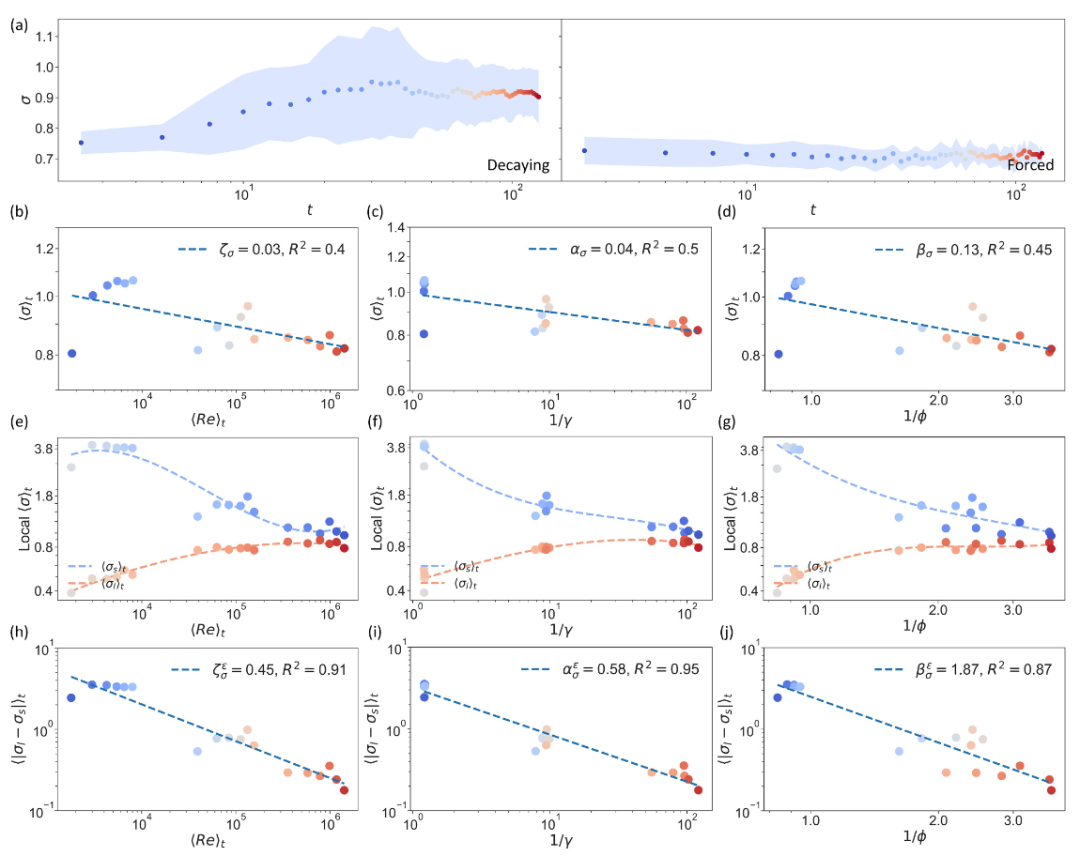
📏 研究发现,流体中涡旋的空间分布具有自相似性,高湍流性(大雷诺数)条件下更显著,低湍流性时自相似性逐渐消失,且自相似性指数受动能和涡度衰减速率影响。
🔄 通过重整化群变换,发现高湍流性条件下涡旋网络尺度不变性更强,表明高湍流性流体系统更倾向于保留多尺度特性。
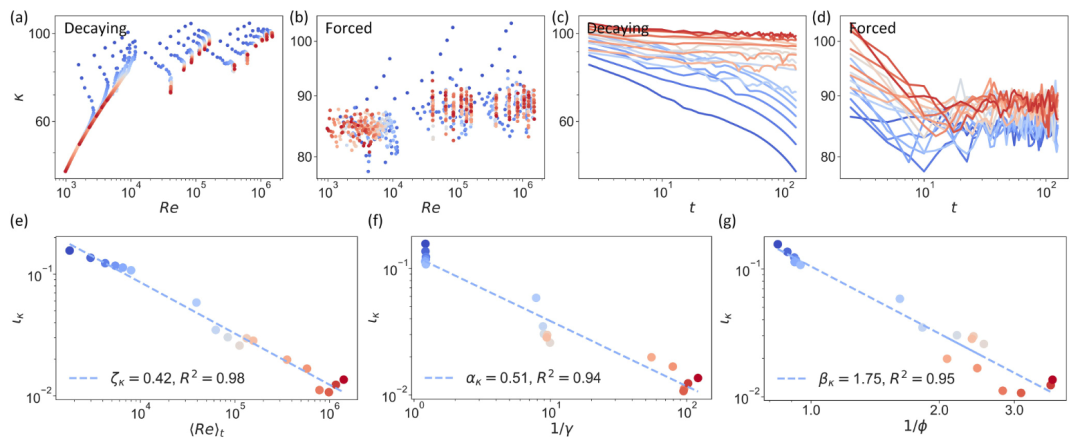
📉 研究定义了“控制标度”,发现控制流体的难度随时间呈幂律衰减,但在高湍流性条件下衰减不明显,表明高湍流性流体控制更难。
关键词:流体网络,复杂网络,空间自组织,重整化群,尺度不变性
论文题目:Fluid-network relations: Decay laws meet with spatial self-similarity, scale invariance, and control scaling论文地址:https://journals.aps.org/pre/abstract/10.1103/PhysRevE.110.064314
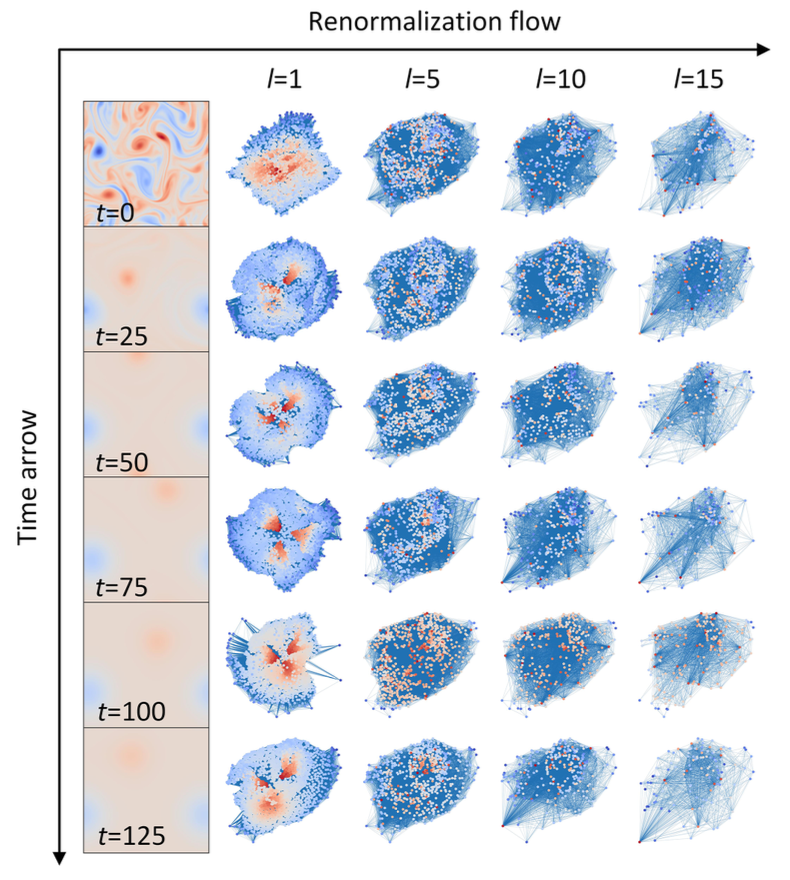
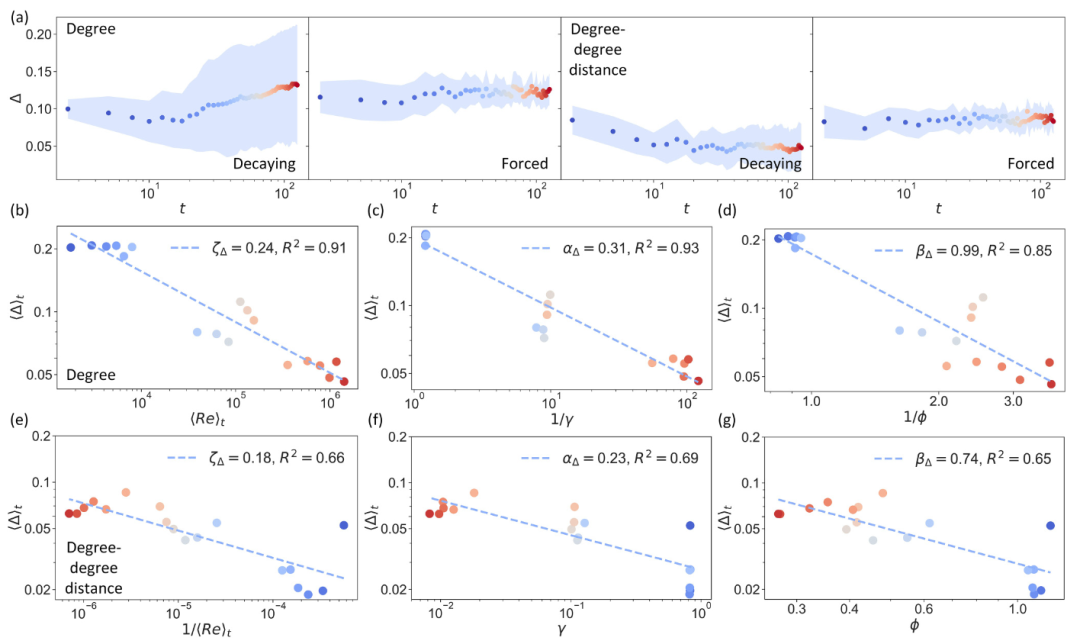
流体中的涡流和湍流通常被看作是无序、混沌且不可预测的,传统的研究方法多集中于流体动力学方程。然而,近年来,研究者们开始探索流体的隐性结构,例如流体中涡旋的相互作用模式。近期发表在 Physical Review E 上的一篇研究提出从网络分析的视角,将流体涡旋之间的相互作用描述为节点和边,构建出流体网络。这项研究揭示流体运动隐藏的空间和拓扑特性,为理解流体动力学开辟了新方法。在构建流体网络的过程中,研究将流体中的每个涡旋视为网络中的一个节点,而涡旋之间的相互作用则构成网络中的边。网络中,每个节点的“度”反映了该涡旋与其他涡旋的联系强度。通过耦合分析流体动力学特性(如动能和涡度)与网络拓扑特性,研究以动能和涡度的随时间衰减规律作为描述流体系统的重要指标,同时重点关注涡旋网络的空间自相似性和尺度不变性等关键特性。研究首先发现,流体中涡旋的空间分布具有显著的自相似性特征,即大涡旋和小涡旋在不同尺度上的分布规律相似。进一步分析表明,自相似性指数直接受到动能和涡度衰减速率的影响:在高湍流性(即大雷诺数)条件下,自相似性更加显著;而随着湍流性的减弱,涡旋的自相似性逐渐消失。此外,研究还揭示了涡旋网络中的连接不平衡性(degree-degree distance)体现了广义空间自相似性。这种广义自相似性在高度湍流的条件下表现最为明显;而当小涡旋快速消散时,这一特性也逐渐被破坏。为了进一步探讨流体网络在不同尺度下的表现,研究对流体网络进行了重整化群(Renormalization Group, RG)变换,发现涡旋网络的尺度不变性在高湍流性条件下更强,体现为涡旋的多尺度结构。这表明,高湍流性流体系统更倾向于保留多尺度特性;而在低湍流性条件下,尺度不变性逐渐丧失。此外,研究还定义了“控制标度”,用于量化控制涡旋网络的难度。结果显示,控制代价随时间呈幂律衰减,即随着时间推移,控制流体的难度逐渐降低。然而,在高湍流性条件下,这种控制代价的衰减变得不明显,趋于时间不变。这表明,在高湍流性流体中,由于其高度不稳定性,对系统进行有效控制更加困难。通过构建和分析涡旋网络,研究揭示了流体动力学特性与网络拓扑特性之间的深刻联系。流体系统中的动能耗散、涡旋分布的自相似性和控制难度等现象可以通过复杂网络的方法进行深入解析。这项研究不仅为理解复杂流体系统提供了全新的理论视角,也为工程中的流体控制和优化设计提供了重要的理论依据。图 1. 流体数据处理流程图。给定一系列随时间变化的涡旋场,提取其对应的流体网络,并对这些流体网络进行多次迭代重整化。
彭晨 | 编译
详情请见:从热力学、生命到人工智能的统计物理之路:非平衡统计物理读书会启动!
6. 加入集智,一起复杂!
内容中包含的图片若涉及版权问题,请及时与我们联系删除