今天为大家介绍的是来自北京科技大学宿彦京团队发表的一篇论文。机器学习势能（MLPs）已经表现出显著的精度，但缺乏适用于广泛元素及其合金的通用型MLPs，限制了其应用范围。在本文中，作者构建了一个适用于多种元素的统一通用MLP，并通过一个针对16种金属元素及其合金的模型（UNEP-v1）进行演示。为了实现化学空间的完整表征，作者通过主成分分析和多样化的测试数据集，证明采用单组分和双组分系统就足以完成这一任务。该统一模型UNEP-v1在多个物理性质上展现出优于广泛使用的嵌入原子法势能的表现，同时保持了卓越的计算效率。通过再现实验观测到的化学顺序和稳定相，以及在MoTaVW合金中进行大规模的塑性和主要辐射损伤模拟，作者展示了该方法的有效性。

元素金属及其合金的原子级模拟对理解和设计材料性质至关重要。量子力学方法如密度泛函理论（DFT）适用于小规模模拟，但在大规模时其可行性下降。对于大规模经典原子模拟，分子动力学（MD）和蒙特卡罗（MC）模拟依赖于原子间势能。嵌入原子法（EAM）势能在金属系统中应用广泛，但现有势能在精度上存在不足。近年来，基于机器学习（ML）技术的原子间势能模型因其更大的拟合参数和灵活的功能形式，表现出比传统势能更高的精度。

MLP的核心理论已相对成熟，主要包括回归模型和输入描述符。常用的回归模型包括线性回归、人工神经网络（NN）回归和基于核的回归。尽管MLP精度更高，但其计算成本相对较高，且缺乏覆盖多种元素及其化合物的数据库。此外，不同元素的MLP尚无法简单组合以构建合金的模型。为解决这些问题，神经进化势能（NEP）方法通过优化理论形式和高效实现，提高了计算效率，适用于大规模模拟。

本文基于NEP3方法，提出了专门针对多组分系统的扩展方法，命名为NEP4，并在GPUMD版本3.8中实现。首先简要介绍NEP3，它是一个神经网络势能模型，将中央原子的描述符向量qi映射到其位能Ui。系统的总能量为各原子位能之和。该ML模型是一个单隐藏层的全连接前馈神经网络，输入为描述符向量qi，输出为位能Ui，并采用双曲正切（tanh）作为激活函数。

将神经网络中的权重和偏差参数统称为w，则系统总能量正式表示为：

描述符向量包含径向和角度组件，本文使用最多五体角度组件。以三体角度组件为例，它可以表示为：

其中gn(r)为径向函数，Pl(x)为勒让德多项式，rij是原子间的距离，θijk为三原子角度。通过线性组合的方式，径向函数gn(r)由若干基函数fk(r)构成，保证模型的完备性和光滑性。

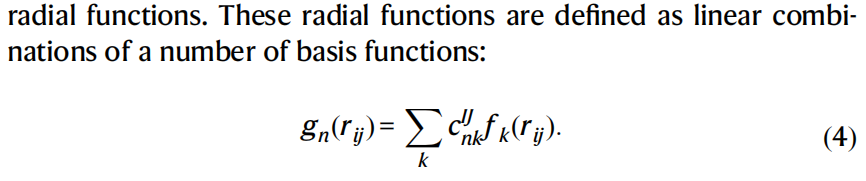
在NEP3中，所有原子类型共享相同的神经网络参数。为了提高回归能力，本文为每种原子类型引入不同的神经网络参数wI，从而保持每种原子类型的回归能力。该扩展使得位能可以表达为：

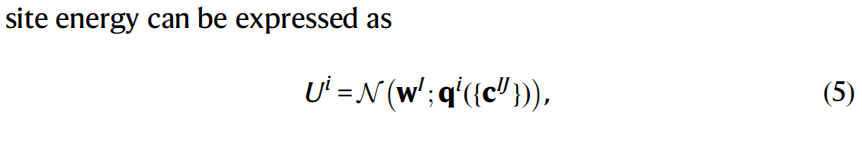
这就是本文提出的NEP4模型（图1a）。

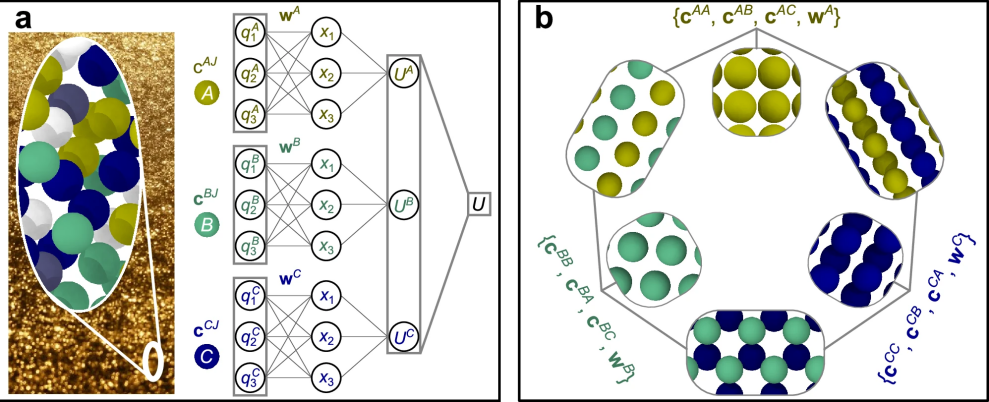
图 1

随着可训练参数的增加，尤其是使用NEP3时训练所需的迭代次数显著增加。为了提高多元素系统的训练性能，作者采用了可分离自然进化策略（SNES）方法，这是一个适合多解问题的强大优化算法。该算法为每个可训练参数维护均值和方差，并根据解的排名进行更新，排名基于损失函数。

损失函数L由预测能量、力和体积数据与参考数据构成，函数表达式如下：

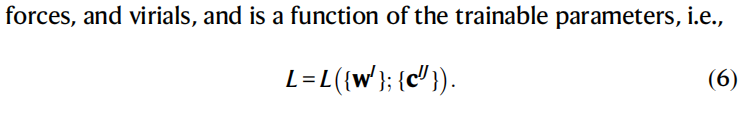
在进化算法中，排名（或“适应度”）至关重要，它决定了解的相对权重。但使用单一损失函数可能导致排名模糊。举例来说，方案X的总损失小于方案Y，但这并不意味着方案X在所有子系统中更准确。为了解决这个问题，作者为多元素系统定义了多个损失函数。考虑到合金系统，作者定义了针对每种元素的损失函数以尽量减少公共项。例如，元素A的损失函数仅考虑含有元素A的结构，如 A、AB和AC，而不包括B、C和BC。如图1b所示，该损失函数在训练包括wA、cAA、cAB和cAC等与元素 A 相关的参数时使用。使用这种多损失进化算法，训练收敛速度比单一损失函数更快，随着元素数量的增加，效率提升更加显著，这对于开发如UNEP-v1这样的模型至关重要。

16种元素的化学空间包含65535种化学组合，包括16种单组分、120种双组分、560种三组分等。通过枚举所有可能的化学组合来构建训练数据集非常困难。幸运的是，利用径向函数的基函数线性组合可以解决这一问题。对于给定的n组分（n>2）系统，其描述符值落在由1组分和2组分系统的描述符值所覆盖的范围内，因此通过1组分和2组分结构训练的NEP模型可以较好地预测n组分系统的行为。因此，作者的训练数据集仅集中在单组分和双组分系统。

初步训练数据集的多样性确保了一个稳健的初步NEP模型，可用于在各种热力学条件下进行MD和混合蒙特卡罗与分子动力学（MCMD）模拟。从初步NEP模型生成的多样MD和MCMD轨迹中，提取并标记了结构（仅限单组分和双组分），并通过DFT计算检查误差较大的结构。通过反复迭代此过程，直到未检测到大误差。这个简单而有效的主动学习方案最终得到了包含105464个结构和6886241个原子的训练数据集。DFT计算耗费了约600万CPU小时。

通过精化后的训练数据集，作者使用NEP4方法训练了一个NEP模型，称为UNEP-v1，这是构建通用NEP模型的首次尝试。UNEP-v1模型在能量、力和应力的平衡图（图2a–c）中显示了高精度。尽管这三种量的范围较大，其均方根误差（RMSE）分别为17.1 meV atom⁻¹、172 meV Å⁻¹和1.16 GPa，均较小。

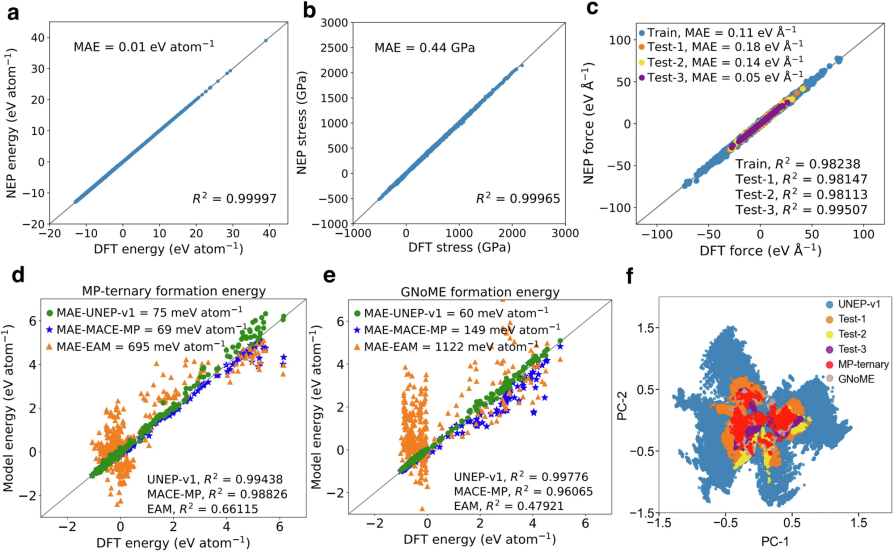
图 2

为了验证UNEP-v1模型的力学准确性，作者使用了三个公共数据集，尽管计算设置略有不同，力值差异非常小（约几个meV Å⁻¹），远小于UNEP-v1的RMSE（图2c）。此外，UNEP-v1模型对1组分和2组分结构的训练同样适用于3组分、4组分和13组分结构，验证结果显示，模型的RMSE分别为76 meV Å⁻¹、196 meV Å⁻¹和269 meV Å⁻¹，与原始文献中的训练RMSE相当。

在能量准确性验证方面，作者利用了两种公共数据集，并将UNEP-v1模型与DFT计算、EAM势能和MACE-MP-0模型进行了比较。UNEP-v1的平均绝对误差（MAE）分别为75 meV atom⁻¹和60 meV atom⁻¹（图2d, e），而EAM模型的误差大约高一个数量级。对于Materials Project数据集，虽然MACE-MP-0表现稍好，但对于GNoME数据集，UNEP-v1显示了显著更好的准确性。

进一步的测试表明，加入多组分结构后，训练的NEP模型在RMSE上与UNEP-v1的表现几乎没有差异，说明使用1组分和2组分结构的训练数据集已足够用于训练通用NEP模型。通过主成分分析（图2f），作者展示了径向函数所嵌入的化学泛化特性，验证了1组分和2组分结构的训练数据集能够有效覆盖更高组分的结构空间。

在确认UNEP-v1模型对于1组分和2组分系统的高训练精度及其对多组分系统的高测试精度后，作者进一步评估了UNEP-v1模型在基本物理性质方面的表现。作者计算了16种元素的弹性常数Cij、表面形成能γ、单空位形成能Ev、熔点Tm和声子色散关系，并与EAM势能进行了比较。尽管有一些较新的、可能更精确的EAM势能，但作者仍选用了Zhou等人开发的广泛使用的EAM势能，因为它支持所有16种元素及其合金。

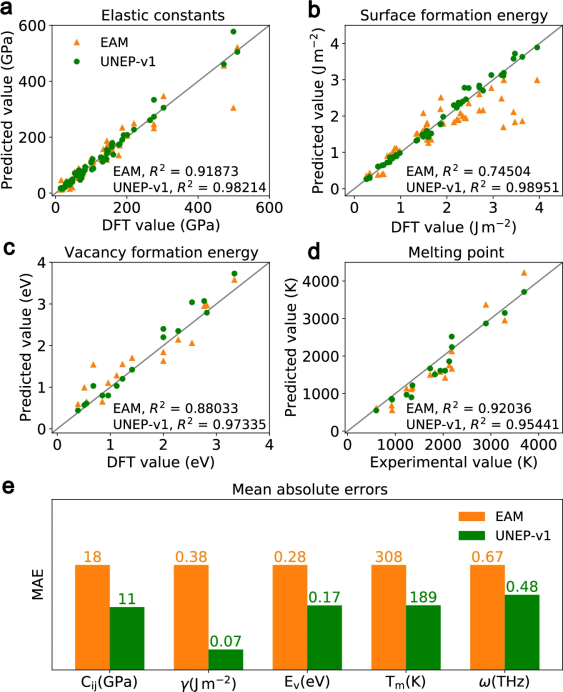
图 3

图3a–d显示了EAM和UNEP-v1模型对各种基本物理性质的预测与DFT计算或实验值的比较平衡图。EAM的预测有一些离群值，特别是在表面形成能方面，而UNEP-v1的预测没有显著差异。图3e显示了对16种元素所有评估量的平均绝对误差（MAE）。UNEP-v1模型在所有物理性质上均优于EAM势能，特别是在表面形成能、弹性常数和空位形成能的预测上，表现出了显著优势。

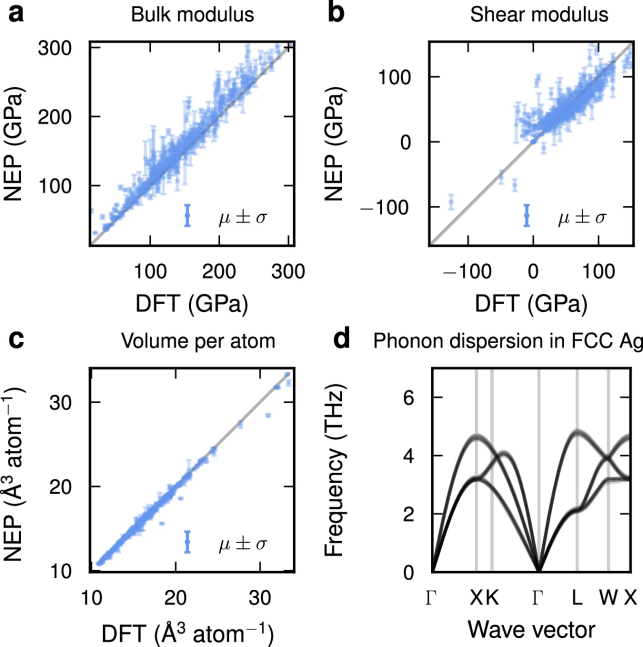
图 4

为了进一步验证，作者在图4a-c中训练了八个不同训练超参数集合的NEP模型集，并比较了模型集对体积模量、剪切模量和平衡体积的预测与DFT参考数据的差异。一般来说，模型集中的预测偏差较小，并且与参考数据高度一致。作为进一步的示例，图4d展示了银（Ag）声子色散的预测不确定性，结果表明，在整个布里渊区内的预测不确定性非常小。

耐火MPEAs（多主元素合金）因其在超高温下出色的延展性和机械强度，已成为高温应用材料的研究热点，通常在BCC固溶体相中结晶。然而，它们在室温下的延展性较差。近期实验发现，合金如HfNbTaTiZr中存在大量直线螺位错和位错残余，这与BCC金属的已知行为一致。分子动力学模拟也显示，位错在MPEAs的塑性流动中可能起着关键作用。尽管已有一些针对特定合金的MLP模型，但目前仍缺乏一个能涵盖广泛元素及其合金、提供高效性和准确性的通用模型，以支持大规模（高达百万原子）MD模拟。

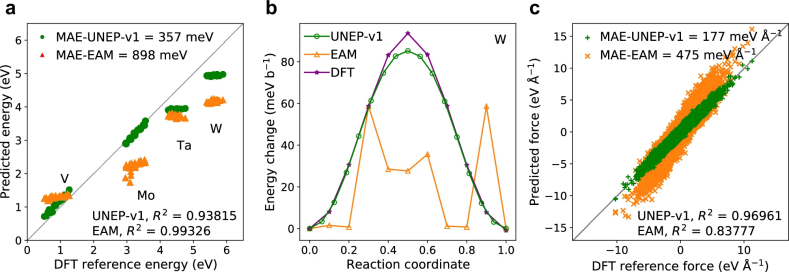
图 5

本文开发的UNEP-v1模型能够进行大规模的MPEAs MD模拟，且在精度上优于现有模型，同时保持高计算效率。为验证其有效性，作者研究了MoTaVW合金在压缩下的塑性变形机制。通过对UNEP-v1模型的评估，作者进行了全面的测试，包括在等摩尔MoTaVW合金中的空位形成能（图5a）、1/2螺位错的Peierls势垒（图5b）以及熔化过程中的原子力（图5c）。结果显示，UNEP-v1在预测结构和机械性质方面表现优于EAM势能，适合于大规模MD模拟。

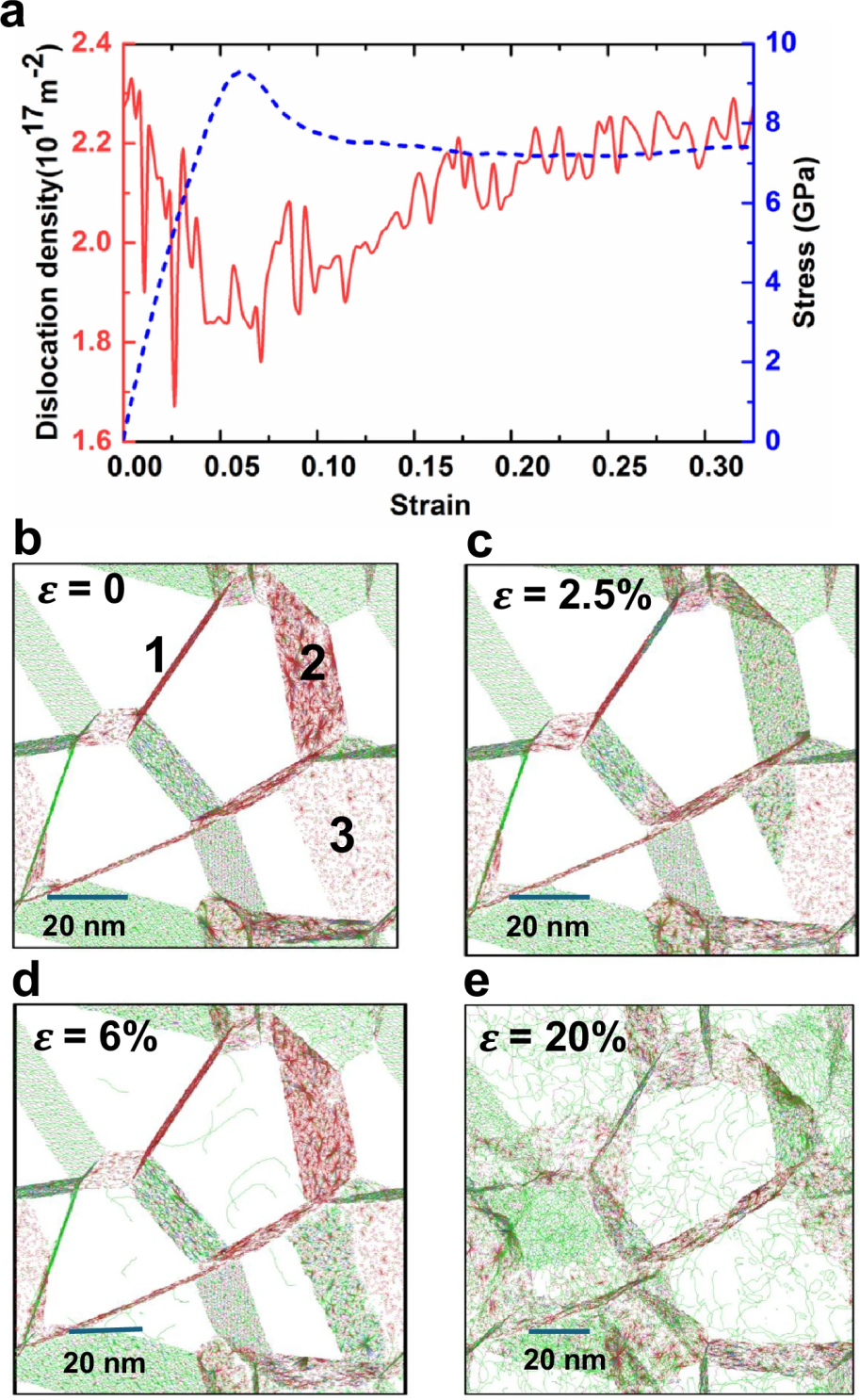
图 6

接下来，作者模拟了含有100,205,176个原子的等摩尔BCC多晶MoTaVW系统，并进行了MD模拟以研究压缩下位错密度的变化（图6a）。在弹性阶段，位错密度减少，并在屈服应变（6%）时达到最小值，随后由于密实度增强而逐渐恢复。对于大应变（ϵ ≥ 16%）的情况，位错密度趋于稳定，符合BCC-Ta的实验行为。

为进一步深入了解塑性变形机制，作者提取了在选定应变下的多晶MoTaVW系统中的位错密度分布（图6b–e）。在压缩过程中，所有位错都被局限在多晶系统的晶界内，并且这一模式在应力-应变曲线的线性响应（弹性）区域保持不变。在弹性区域内（0-2.5%），位错从其他类型转变为1/2螺位错，并在屈服应变（6%）时恢复。进入塑性阶段后，部分晶界开始发射、滑移，并将位错固定在晶粒内，显示出边界稳定性对MPEAs硬度的显著影响。

通过百万原子规模的MD模拟，作者揭示了塑性变形的复杂细节，特别是位错在晶界中的行为。UNEP-v1模型在MoTaVW合金塑性研究中的应用，展示了该方法的通用性和高计算效率。

为了展示UNEP-v1模型的多功能性，作者通过大规模MD模拟研究了MPEAs中的初级辐射损伤，使用MoTaVW合金系统作为示例。为准确描述短距离内的强相互作用力，作者引入了双体Ziegler-Biersack-Littmark（ZBL）势能，训练了一个结合NEP-ZBL模型。UNEP-v1和ZBL部分在1到2Å之间平滑连接，2Å以上仅激活UNEP-v1部分，1Å以下则由ZBL部分主导。

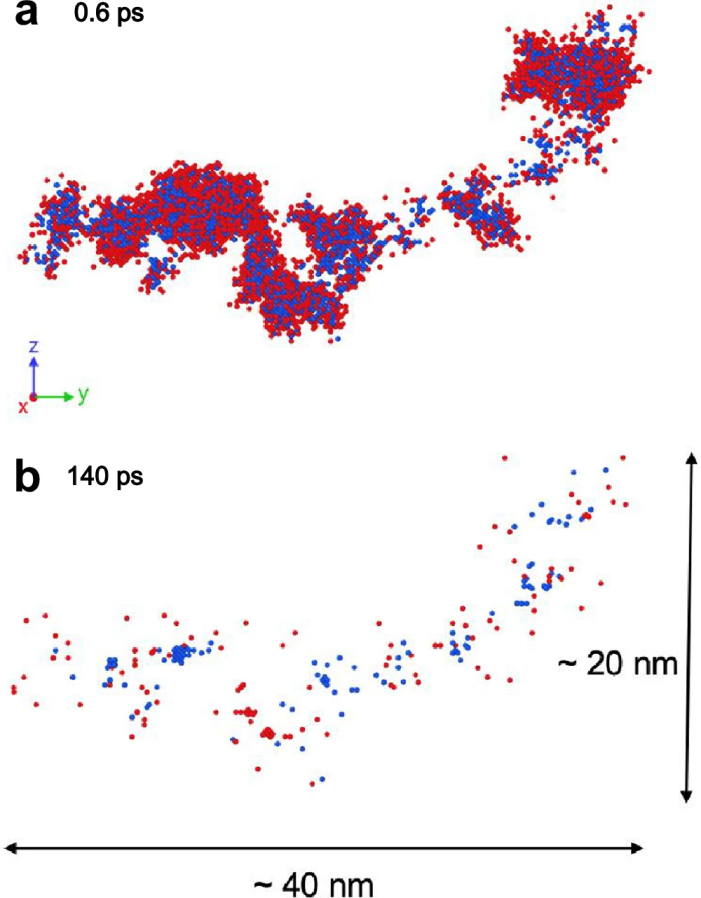
图 7

图7a显示了在初级打击原子能量为100 keV、约0.6 ps时形成的缺陷快照。经过几十个皮秒后，缺陷分布趋于稳定。图7b展示了在140 ps时稳定的缺陷分布，共有121个残余点缺陷，包括空位和间隙原子。空位和间隙原子的最大簇大小分别为15和11。相比之下，先前对元素W的研究在类似条件下报告了183个残余点缺陷，最大缺陷簇的大小超过200个原子。因此，MPEAs的缺陷数量较少，缺陷簇较小。模拟结果与类似的钨基耐火MPEA实验研究一致，该材料展现了卓越的辐射抗性、几乎无辐射硬化，并且即使在高剂量下也没有辐射诱导的位错环。通过对1600万原子的MD模拟，作者进一步证明了UNEP-v1模型在研究初级辐射损伤中的通用性和高效率。然而，仍需要更详细的研究来全面了解合金化在影响辐射抗性中的作用。

作者展示了UNEP-v1模型在大规模MD和MCMD模拟中的可靠性，并与EAM模型结果和实验数据进行了详细比较。以下是三个应用的示例：

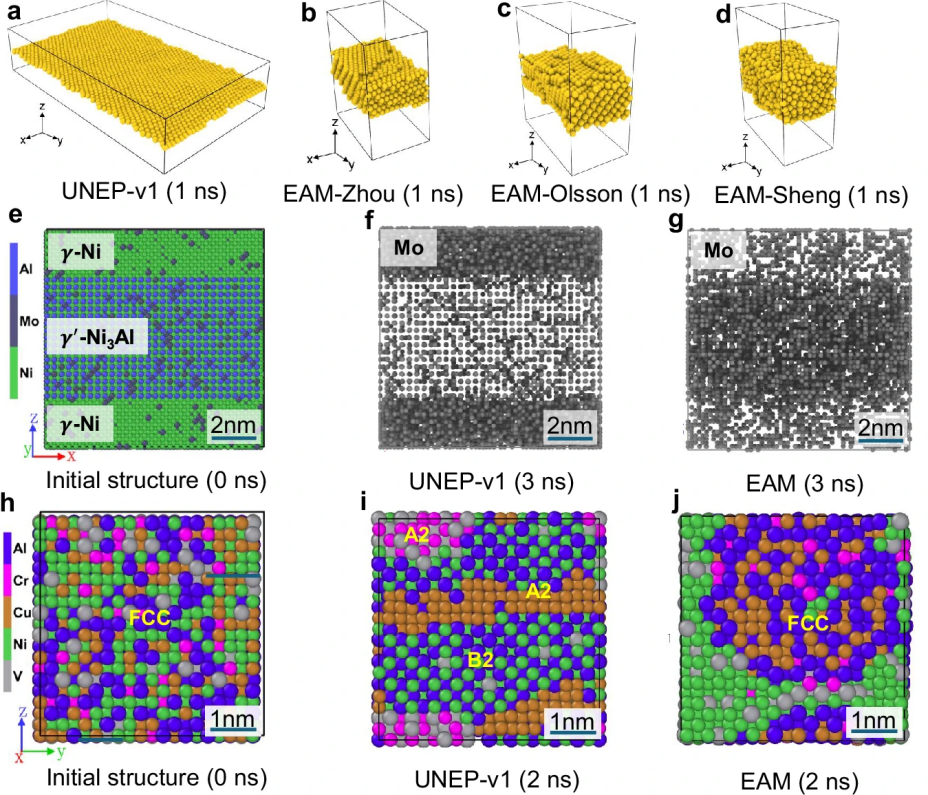
图 8

1. 金烯（goldene）模拟：作者使用UNEP-v1对金烯（一种金的单层形式，未包含在训练数据集中）进行了MD模拟。金烯的稳定结构为三角形晶格（图8a）。在300 K下，UNEP-v1能够保持金烯片层的稳定性，展示了典型的二维材料的翘曲。相比之下，使用文献中EAM势能的模拟结果（图8b-d）显示，金烯单层结构无法保持稳定。该结果证明了UNEP-v1模型在配置空间中的良好泛化能力。

2. Mo分布的MCMD模拟：在γ-Ni和γ'-Ni3Al的超晶格结构中，作者使用MCMD模拟研究了Mo的分布。初始时Mo的浓度为8.1%（图8e），根据UNEP-v1模型，最终γ'-Ni3Al中的Mo浓度与γ-Ni中的比值为Kγ' /γ = 0.667（图8f），与实验观测结果一致。相比之下，Zhou等人的EAM势能（图8g）给出了Kγ' / γ = 4.981的值，与实验趋势相悖。

3. 富铝金属间化合物的MCMD模拟：作者使用MCMD模拟重现了实验上预期的BCC结构，尽管初始时含有大量FCC金属（图8h）。UNEP-v1模型成功地生成了无序（A2）和有序（B2）BCC结构（图8i），与实验结果完全一致。而Zhou等人的EAM势能则保持系统在FCC结构（图8j）。类似的结果也出现在Al0.20Cr0.12Cu0.19Ni0.35V0.14合金中，进一步证明了UNEP-v1模型在可靠性上的优势。

这些结果充分展示了UNEP-v1模型在大规模模拟中的优异性能，相比于EAM模型，能够更准确地捕捉复杂的物理现象。

本文提出了一种先进的NEP方法，能够为多种元素及其合金构建高效且精确的通用MLP。与之前的NEP版本相比，做出了两项重要扩展：一是为每种元素使用独立的神经网络，确保即使物种数量增加，回归能力也保持一致；二是引入多损失函数，优化不同参数子集，加速训练过程。通过将化学信息嵌入径向函数的可训练扩展系数中，1组分和2组分结构在描述符空间中划定了外边界，n组分（n≥3）结构则作为内插点。UNEP-v1模型在研究MPEAs的塑性和初级辐射损伤中展示了其多功能性和高效性，证明了该方法在材料建模中的应用潜力。

编译 | 于洲

审稿 | 王梓旭

Song, K., Zhao, R., Liu, J. et al. General-purpose machine-learned potential for 16 elemental metals and their alloys. Nat Commun 15, 10208 (2024).