本文探讨了为什么中位选民定理在现实政治中常常失效。文章指出，中位选民定理假设选民的偏好是单峰的且不相关，但在实际情况中，选民的偏好往往是相关的，例如，反对堕胎的选民也往往反对移民。这种相关性导致了政党无法简单地采取中庸路线，而是倾向于代表特定选民群体的偏好。文章通过一个简单的例子说明了这一点，并进一步讨论了排名选择投票制、中位选民定理的适用范围以及议会制国家的情况。最终，文章指出中位选民定理在现实世界中应用的局限性，特别是在涉及复杂政策议题的总统选举中。

🤔**选民偏好的相关性是中位选民定理失效的关键因素。** 例如，在移民和堕胎这两个议题上，选民的观点并非独立存在。反对堕胎的选民往往也反对移民，而支持堕胎的选民往往也支持移民。这种相关性导致了选民偏好的复杂性，使得政党无法简单地选择每个议题上最受欢迎的政策来最大化选票。这种相关性使得政党更倾向于代表特定选民群体的整体偏好，而非简单地追求每个议题上的中庸立场。这就好比一个超市的顾客，他们可能更倾向于购买一个包含多种他们喜欢的商品的礼盒，而不是单独购买每个他们喜欢的商品。这种选民偏好的相关性，使得中位选民定理的适用范围受到了限制，因为它忽略了选民在不同议题上的偏好之间的关联性。如果选民的偏好是独立的，那么中位选民定理或许能更好地描述政治现象，但现实情况并非如此。

🗳️**“先到先得”的选举制度（FPTP）加剧了中位选民定理的失效。** 在“先到先得”的选举制度下，获得最多票数的候选人胜出，这使得候选人更有动力去争取特定选民群体的支持，而非追求所有选民的中庸路线。例如，如果在一个有两个议题的选举中，有四个候选人代表了四个可能的政策组合，那么最有可能获胜的候选人并不是那个在每个议题上都采取中庸立场的候选人，而是那个代表了特定选民群体（例如，反对堕胎和移民的选民）的候选人。因为，即使这个候选人在总体上获得的选票数可能不是最多的，但他们可以获得足够多的选票来战胜其他候选人。这种选举制度的设计，使得政党更倾向于形成鲜明的政治立场，以吸引特定选民群体，而非追求中庸路线。这就好比在一个比赛中，如果获胜的标准是获得最多票数，那么选手更有动力去争取特定群体的支持，而非追求所有人的喜爱。

📊**中位选民定理仅适用于单峰偏好和特定投票机制。** 中位选民定理的适用范围非常有限，它只适用于单峰偏好的情况，即所有可能的政策结果可以按照某种标准排序，并且每个选民都对该标准有一个最优的偏好，并且偏离这个最优偏好的程度越高，他们的满意度就越低。例如，如果选举议题是决定移民人数，那么每个选民都会有一个理想的移民人数，并且偏离这个理想人数的程度越高，他们的满意度就越低。在这种情况下，中位选民定理才适用。然而，在现实生活中，许多政治议题的政策结果并非如此简单，例如，决定从哪些国家接纳移民，或者决定一系列复杂的政策组合。在这种情况下，选民的偏好是多维的，并且每个选民对不同政策结果的排序方式都可能不同，中位选民定理便不再适用。

🌍**议会制国家中，政党更有动力迎合特定选民群体。** 在议会制国家，选举结果往往不是产生一个单一的赢家，而是产生一个议会，并且除非一个政党获得绝对多数的选票，否则政府通常是由多个政党组成的联合政府。在这种情况下，政党更有动力去迎合特定选民群体，因为他们可以通过精准满足这些选民的诉求，从而获得他们的支持，从而确保他们在议会中占据席位。而试图采取中庸路线的政党则很可能失去所有选民的支持。这就好比在一个市场上，如果有多个商家可以满足不同的顾客需求，那么商家更有动力去迎合特定顾客群体的需求，而非追求所有顾客的平均需求。

Published on November 3, 2024 2:03 PM GMT

Scott asks why, if the Median Voter Theorem is true, American politicians aren't all middle of the road, and barely distinguishable from each other.

Elegant as this proof may be, it fails to describe the real world. Democrats and Republicans don’t have platforms exactly identical to each other and to the exact most centrist American. Instead, Democrats are often pretty far left, and Republicans pretty far right. What’s going on?

He suggests a number of reasons. And they're all probably true at the margin. But there's a much more basic reason why parties aren't clones of each other: preferences are correlated.

I'm going to give a really simple toy example, and we're going to see that correlated preferences + first pass the post is enough to blow the Median Voter Theorem out of the water.

Let's pretend there's only two issues that matter to the American voter. Immigration, and Abortion. And let's pretend that these issues are binary - they're either fully legal, or completely banned^[1].

40% of voters want abortion to be banned, and 60% want it to be legal.

60% of voters want immigration to be banned, and 40% want it to be legal.

But opinions on these two issues are not uncorrelated. Almost nobody is against abortion, but loves immigration. Pretty much everyone who wants abortion to be banned wants immigration to be banned, and everyone who want immigration to be legal wants to abortion to be legal.

So voter preferences look like this.

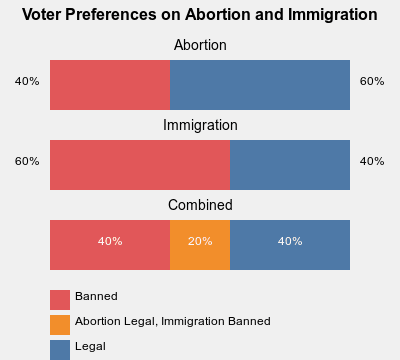
Now, if we wanted to satisfy the most preferences, under reasonable assumptions^[2] we should ban immigration.

But if you had 4 candidates, representing each of the 4 possible policy choices, the one who advocated this policy would come in a distant third:

Candidate	Abortion Policy	Immigration Policy	Voter Support
A	Banned	Banned	40%
B	Legal	Legal	40%
C	Legal	Banned	20%
D	Banned	Legal	0%

I think this models the real world pretty well. Republicans and Democrats don't just differ a bit on the details, they represent baskets of policies, each of which the majority of their voters want. A party that chose the most popular option for each policy would be less tempting both to democrats and to republicans than their current party.

Other Related Stuff

That's the gist of the post over, view this as an appendix.

Ranked Choice Voting

I think that ranked choice doesn't have this problem^[3], but haven't yet put in the time to prove it for the general case: e.g.

Let's assume that when picking a 2nd/3rd choice candidate 50% of voters care about abortion more and 50% care about immigration more. Then we get this:

Candidate	1st choice	2nd choice	3rd choice	4th choice
A (ban/ban)	40%	10%	10%	40%
B (leg/leg)	40%	10%	10%	40%
C (ab leg/im ban)	20%	40%	40%	0%
D (ab ban/im leg)	0%	40%	40%	20%

If we give 1 point to 3rd choice, 2 for second and 3 for 1st we would end up with scores:

Candidate	Score
A (ban/ban)	150 (403 + 102 + 101)
B (leg/leg)	150 (403 + 102 + 101)
C (ab leg/im ban)	180 (203 + 402 + 401)
D (ab ban/im leg)	120 (402 + 40*1)

Median Voter Theorem doesn't apply to First Pass The Post

The Median voter theorem only applies to voting mechanisms where if a candidate would be preferred to everyone else in a head to head match, they would also win in a multi-candidate match. This doesn't apply to FPTP where two similiar candidates can split the vote, letting a less preferred candidate win.

Median Voter Theorem basically never applies

The Median Voter Theorem only applies to single peaked preferences. This means that all possible outcomes can be ordered from most X to least X, and everybody just picks an amount of X they want.

So for example, the Median Voter Theorem would apply if everybody was voting on how many immigrants should be let into the country, since then everybody picks a number, and the further away the number of immigrants is from this number the sadder you are.

But it wouldn't apply if everybody was picking which countries to let immigrants in from, because everybody would rank them in different orders - some people would say the only people we should let in are Canadians, others might say Japanese or Europeans or whatever.

And it definitely definitely definitely doesn't apply to Presidential elections where you're voting on an incredibly broad set of policies, each of which people will have their own complex opinions on.

Median Voter Theorem is kind of trivial

As discussed, the Median Voter only applies when:

a) If a candidate would be preferred to everyone else in a head to head match, they would also win in a multi-candidate match.

b) All possible outcomes can be ordered from most X to least X, and everybody just picks an amount of X they want.

At which point it's obvious the Median candidate will win, because they are preferred to every other candidate in a head to head match (by definition of Median).

Parliamentary Democracies

The Median Voter Theorem only applies when there is a single winner of the election. But most countries don't actually have a single winner - they have a parliament, and unless a single party is preferred by a majority of the electorate over all other parties, the country will usually be ruled by a coalition.

Under these circumstances parties have an incentive to cater to a particular group of people. Since they can almost exactly match what the group wants, they are almost guaranteed their votes. Someone who tries to take the middle of the road approach won't get any votes. If proportional representation is used, you would naively expect there to be as many parties as there are seats, each getting exactly one seat. In practice people vote strategically + vote for the most salient parties, so parties tend to be significantly bigger than this.
 

1. ^{^}

   Whilst this obviously isn't true in real life, in practice the real question tends to be whether to move the current policy a bit more to the left, or a bit more to the right, which ends up as effectively a binary choice for most people, unless you happen to want a position exactly between where it currently is and where it will probably end up if your party wins.

2. ^{^}

   E.g. 
   - Those who want to ban abortion don't feel much more strongly about the issue than those who want to make it legal.
   - People's opinion on about one issue doesn't depend on what policy is chosen for the other, so if you make abortion legal, nobody will as a result change their mind about immigration.

3. ^{^}

   For any implementation where score per ranking is linear in the ranking. After all FPTP is just a degenerate ranked choice where all ranks below 1st get 0.

Discuss