

关键词:自适应在线学习,量子态学习
导 读
本文是发表在 Quantum 上的论文 Adaptive Online Learning of Quantum States 的详细解读。该项研究由北京大学李彤阳课题组与普林斯顿大学 Elad Hazan 教授课题组合作完成。
论文利用自适应在线学习方法,实现对动态量子态关于量子比特数

论文地址:
https://quantum-journal.org/papers/q-2024-09-12-1471/
01
引 言
量子态的有效学习是量子计算中的一个重要问题。不同于经典的情形,完整刻画
然而以上方法均未涵盖现有量子计算机的一个重要问题:量子态的涨落。在实际场景中,我们通常无法持续校准量子态,例如在 IBM 的量子计算平台上,一个包含测量的量子电路可能连续执行成百上千次,而在这些实验中途不会进行校准。在现实中,量子态
02
问题设定
考虑一个
我们考虑两种度量:动态后悔值和适应性后悔值。
1. 动态后悔值衡量玩家的损失与变化的比较器(comparator)之间的差异,其界限通常由最佳比较器随时间的变化程度(路径长度
2. 适应性后悔值的定义更为精细,其衡量所有时间区间内的最大后悔值,本质上刻画了比较器的变化。在这一设定下,我们考虑量子态在某些时刻发生跳变的情形,相应适应性后悔值的定义是
03
算法设计
最小化动态后悔值 我们提出最小化动态后悔值的 Algorithm 1、2,将不同步长的在线优化算法作为专家策略,并利用乘子权重法选择最优专家,更新权重以找到最佳步长。这一算法设计参考了[2],引入专家算法的需求源于,为了获得动态后悔值界限,学习率必须是路径长度的函数,而路径长度在事先是未知的。值得注意的是,在量子态的学习问题中,直接应用在线梯度下降会导致梯度上界正比于系统维度


最小化适应性后悔值 对于损失函数中

04
理论结果
针对以上两种问题情景下提出的算法,我们证明了相应的后悔值上界(regret bound)和错误次数上界(mistake bound)。
在动态后悔值的设定下,假设路径长度
在适应性后悔值的设定下,同样假设损失函数
此外,我们还考虑了 Algorithm 1 在量子计算实际场景中的应用:假设预先给定
05
数值实验
为了支持我们的理论发现,我们开展了一系列数值实验以验证所提出模型的有效性。
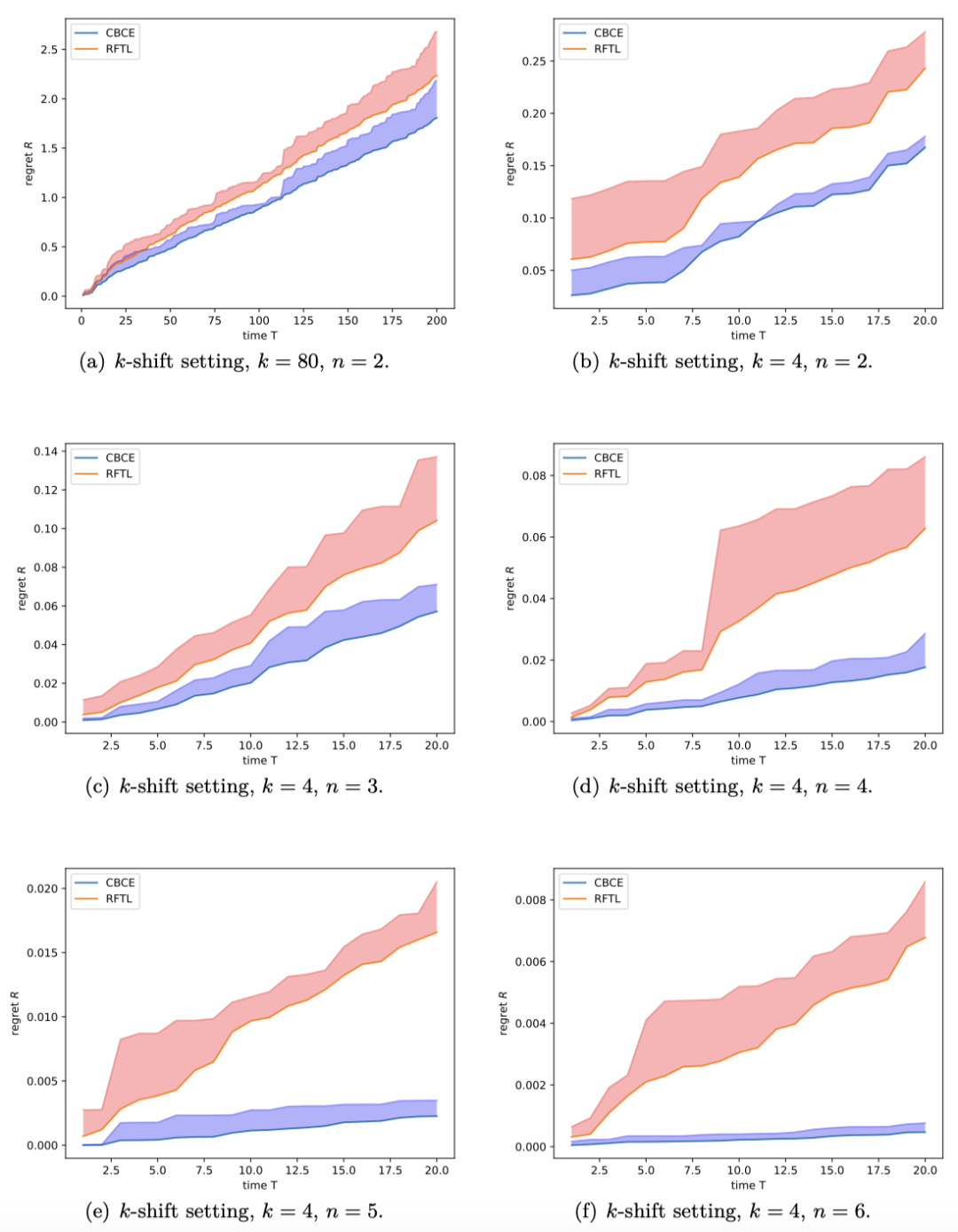
与非自适应算法的对比 自适应在线学习算法的一大显著优势在于捕捉量子态的动态变化。此前的算法如 RFTL 对于固定量子态有良好的预测能力,但不能很好适应量子态演化。我们比较了 RFTL 算法与我们的 Algorithm 3在量子态发生k次跳变的情形下累积的适应性后悔值,结果如下图所示。“CBCE”代表 Algorithm 3,“RFTL”为非自适应算法。两条曲线表现出相似的趋势,但 Algorithm 3实现了更小的后悔值。在子图 (b)-(f) 中可以明显看出,随着
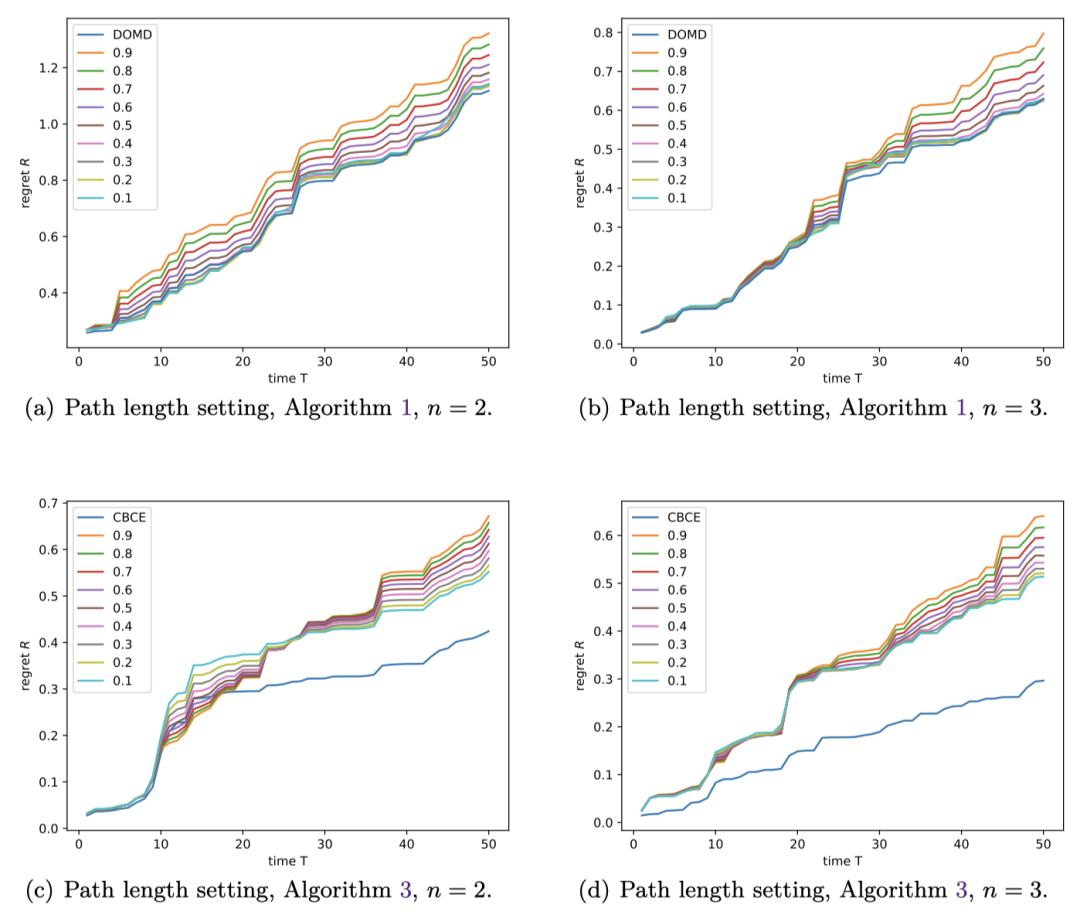
在路径长度有界的设定下,算法的动态后悔值随时间变化如下所示,其中“DOMD”对应我们的 Algorithm 1,“CBCE”对应 Algorithm 3,0.1-0.9的数字对应不同学习率的非适应性 RFTL 算法,类似地可以观察到自适应算法的优势。
后悔值上界的验证 我们还开展了实验用于验证后悔值的上界。
后悔值表征算法预测与最佳值差距在
在子图(b) 中,为了精确验证上界,我们绘制了比值

在路径长度有界的设定下,实验取得了类似的结果,从而验证了算法的理论上界。
06
结 论
本文利用适应性在线学习方法,为可变量子态的确定提供了有力的理论上界。后续工作会进一步对此方法进行拓展和完善,并探索 regret 值的下界、单步测量的不同量子态遵循不同动态演化等开放问题。
参考文献
[1] Elad Hazan, Introduction to online convex optimization, Foundations and Trends® in Optimization 2 (2016), no. 3-4, 157–325, arXiv:1909.05207.
[2] Lijun Zhang, Shiyin Lu, and Zhi-Hua Zhou, Adaptive online learning in dynamic environments, Advances in Neural Information Processing Systems, vol. 31, 2018, arXiv:1810.10.
[3] Scott Aaronson, Xinyi Chen, Elad Hazan, Satyen Kale, and Ashwin Nayak, Online learning of quantum states, Advances in Neural Information Processing Systems, vol. 31, 2018, arXiv:1802.09025.
[4] Kwang-Sung Jun, Francesco Orabona, Stephen Wright, and Rebecca Willett, Improved strongly adaptive online learning using coin betting, Artificial Intelligence and Statistics, pp. 943–951, PMLR, 2017, arXiv:1610.04578.

图文 | 杨睿、王昕兆
PKU QUARK Lab
关于量子算法实验室
量子算法实验室 QUARK Lab (Laboratory for Quantum Algorithms: Theory and Practice) 由李彤阳博士于2021年创立。该实验室专注于研究量子计算机上的算法,主要探讨机器学习、优化、统计学、数论、图论等方向的量子算法及其相对于经典计算的量子加速;也包括近期 NISQ (Noisy, Intermediate-Scale Quantum Computers) 量子计算机上的量子算法。
实验室新闻:#PKU QUARK
实验室公众号:
课题组近期动态


— 版权声明 —
本微信公众号所有内容,由北京大学前沿计算研究中心微信自身创作、收集的文字、图片和音视频资料,版权属北京大学前沿计算研究中心微信所有;从公开渠道收集、整理及授权转载的文字、图片和音视频资料,版权属原作者。本公众号内容原作者如不愿意在本号刊登内容,请及时通知本号,予以删除。

点击“阅读原文”转论文链接

