来源:雪球App,作者: T6584,(https://xueqiu.com/3211767709/304584531)

本周CCFI下跌4.9%,SCFI下跌215.63,加速下跌的趋势并没有改变的迹象,目前还没有看到运价拐点出现的迹象。
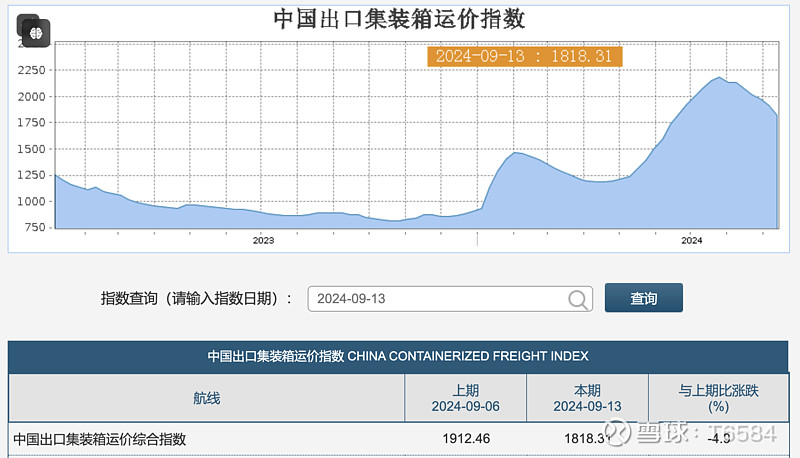
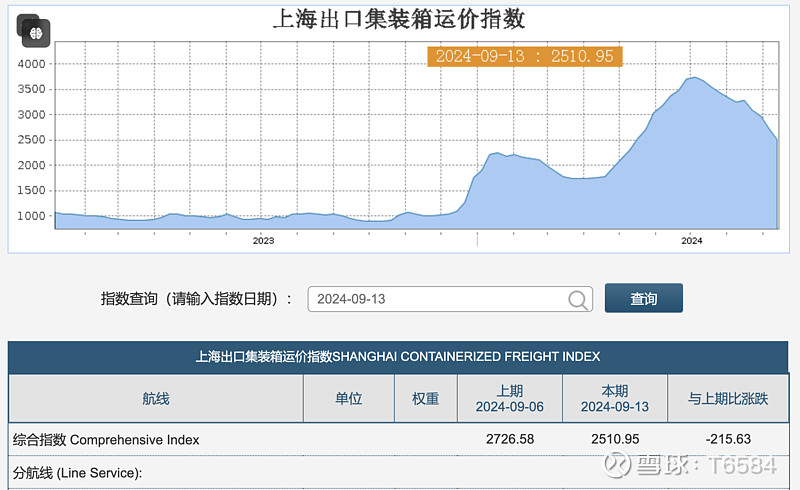
虽然运价没有企稳的迹象,但股价在经历了一周又一周的下跌后,本周表现尚可,似乎有了止跌回升的趋势。
但这究竟是起死回生还是回光返照呢?
不知道
在持有海狗的过程中,很多水手都有过各种各样的疑问。
CCFI的涨跌具体能影响海狗多少?
欧线期货究竟和海狗股价有什么关系?
外围集运股的涨跌与海狗走势的关系是什么?
······
与此类似的问题还有很多,如何判断呢?
在我看来,核心就在于你要知道:相关关系并不等于因果关系。
于是,本周给水手们推荐一本查尔斯·惠伦的《赤裸裸的统计学》。
这是一本有关统计学的书籍,但它不是教你统计学基础原理的教科书,书中的确在一些案例中附带了计算过程和公式来阐述其原理,不过好在这些公式和计算过程并非高等数学中天书一般的密码,所以大可不必太担心,即便跳过也不会影响整体的阅读效果。

查尔斯·惠伦是美国达特茅斯大学教授,1997 到 2002 年间担任《经济学人》杂志驻美国中西部地区记者。他的这本《赤裸裸的经济学》是畅销多年的经济学普及读物。
我读这本书的时候,被书中很多有趣的案例所吸引,同时觉得受益匪浅。因为本书从统计学的角度揭示出了生活中那些反常识现象的根本原因,同时也为我们揭示了人们是如何利用统计数据来欺骗他人的。
正如马克·吐温的一句名言:谎言有三种:谎言、该死的谎言,以及统计学。
数据本身并不会撒谎,但不同的数据处理方式却会令其具有欺骗性。讲一个我自己的段子:
多年前的一天,我和一个同事聊天,谈论的主题是深圳的房价。这其中当然少不了对工资低的抱怨和房价高的抨击,接着也就自然而然的开始抱怨社会的不公平。
就在这个时候,我跟同事说:“你看,我和你还有咱们领导,我们三个人一共有三套房,这算下来不正好人均一套房呢。所以你看,这不也挺公平的嘛,大家不都有一套。”
想必大家也都猜到了这背后的真相,那就是领导有三套。
这当然是当时开玩笑的话,不过仔细想想,我们生活中不就正好存在大量这种带有欺骗性质的数据吗?比如城市平均工资的涨幅、再比如人均消费水平的提高。为什么这些数据总是和我们真实的感受不一致,多数原因都在于这些数据的处理方式迷惑了我们。
一组数据(3、4、5、6、102),它们的平均数是24,中位数是5,你认为哪一个数字更能反映这组数字的整体情况呢?想想我刚说的人均一套房的笑话,你肯定已经知道了答案。
利用不同处理方式得出的数据来骗人,这几乎是从古至今屡见不鲜的事。书中列举的一个例子就十分真切的说明了这中现象。
以美国前总统小布什的减税政策为例,根据小布什政府的说法,这一政策将惠及绝大多数的美国家庭。相关政府官员指出,在这项政策推行之后,将会有9200万美国人享受减税待遇,人均减税额超过1000 美元(具体数字应该是1083美元)。
但这个关于减税政策的概括准确吗?《纽约时报》评价说:“数据本身并没有撒谎,只不过有些数据没有发出声音罢了。” 是不是会有9200万美国人将享受减税待遇?答案是肯定的。 那么,这些人中的大部分人都可以少缴纳约1000美元的税款吗?不是的。因为减税额的中位数还不足100美元。
只有数量相对少的巨富们才有资格享受大额减税,而正是这些人拉高了平均值,让人均减税额看起来比绝大多数美国人真正享受到的要高。中位数对异常值并不敏感,因此在这个例子中,如果要看小布什政府的减税政策对普通家庭的影响,中位数可能会是一个更为准确的描述性数据。
回想一下我们在日常工作中,相信很多人在做工作汇报的时候也都或多或少的利用过这种处理数据的方式来撒谎。比如在汇报销售额时,从10万增长到15万,如果单看数值那也就只有5万的增长,如果我们换算成百分比来表示增幅,那就是50%的增长率。虽然两种方式表述的实质内容一样,但显然第二种看上去增幅会更大。
以上这些小套路仅仅是利用统计学进行数据骗局的一个方面,当我读这本书的时候,我发现这本书真正所揭示的理论并非是在教我们如何识别出这些数据骗局,而是告诉我们如何清楚的意识到自己的认知偏见。
制造一个数据骗局和被数据骗局所欺骗,虽然从表面上看完全是两回事,但这其中最本质的原因是一样的,都是因为人类本身所具有的认知偏见。也就是说,我们之所可以制造出数据骗局,之所以会被统计数字欺骗,都是因为我们对于这个世界的认知存在着无法避免的偏见。
所谓偏见就是以偏概全,比如说大家熟知的“贴标签”、“地图炮”这都是一种以偏概全的行为,它们都是用一小部分的样本特性来概括整个群体的特性,比如遇见一个奇葩的人,就觉得这个人所在的省份的人都奇葩。这些都是常见的以偏概全的形式,那么为什么我们会经常出现这种以偏概全的情况呢?
这并非因为人们在人格方面或生理方面有缺陷,而是因为亿万年的进化过程中,我们在用脑方面的不断妥协与平衡。人的认知活动都是由大脑来完成的,可以说人类进化出一个超级大的大脑是人类登顶食物链顶端的必备要素。
但是这样一个超级武器,也同样有它的软肋,那就是对于人类来说它是消耗能量最大的器官。人类能够吃饱肚子的时代并不长,即便是今天依然有吃不饱饭的人。在这样的环境中,我们对于大脑的利用方式当然是以最省力原则来,所以说:人类最佳的用脑方式是能不用脑就不用脑。
这时候你就会发现,为什么“贴标签”、“地图炮”这种行为会很广泛了,因为它为我们提供了一种快速、且省力的方式来认知事物。所以以偏概全虽然不是一个很好的认知方式,但是它却是人类一路进化而来的一种妥协下的平衡方式。
以偏概全还意味着,只要你没有从根本上改变自己的观念,那么无论你的样本容量有多大,偏见都不会消除。就像刚才说的“地图炮”,如果你不从自己看待事物的角度和思维方式上有根本的改变,那么无论你遇到多少这个省份的人,你也不会改变对这个省份的刻板印象。
书中罗列出了在统计学中,我们常犯的五种偏见,相信你在生活中也一定都遇到过这些偏见的真实案例。
选择性偏见
顾名思义是和我们的选择有关,比如说一个针对某一机场消费者展开的调查肯定是存在偏见的,因为选择乘飞机出行的人一般来说会更加富有一些;而在高速公路旁的休息区展开的调查,可能会存在与机场调查结果相反的问题。
此外,由于愿意在公共场合接受采访的人与不喜欢被打扰的人之间也是有差别的,因此这两个调查都有可能存在先天的偏见。假如你在一个公共场合询问100个人是否愿意接受一个小调查,其中有60人表示愿意回答你的问题,那么这60人与剩下的那些匆匆经过你身边、拒绝跟你有眼神接触的40人之间,可能在某些方面存在着巨大差别。
选择性偏见是在我们开始着手时就已经具有的偏见,所以无论在之后的过程中我们进行如何的调整,已经产生的偏见都不会消失。
书中讲述的《文学文摘》在1936年一次失败的民意测验案例可谓是将选择性偏见的特点阐述的淋漓尽致。
《文学文摘》作为当时影响力颇大的新闻周刊,向该杂志的订阅者以及能够从公共档案中查到地址的汽车和电话主人寄去了一份调查问卷,总共加起来有1000万名美国公民收到了这份问卷,这个样本容量在当时算得上是天文数字了。对于民调来说,优质样本越大,结果就越准,因为误差在减小;但是如果样本本身存在问题,那么民调规模越大,“垃圾”就会越堆越多、越堆越臭。
《文学文摘》预测兰登将会以57%的支持率击败罗斯福赢得选举,而事实又怎么样呢?罗斯福获得了60%的选民投票以及多达46个州(总共48个州)的支持,以压倒性优势赢得了选举。《文学文摘》的样本就是典型的“垃圾”:该杂志的订阅者们比普通美国人要富有,因此更有可能投票给保护富人利益的共和党,1936年家中就拥有汽车和电话的选民的投票情况也是如此。
回头看看我们的现实生活,你会发现这样的偏见我们在大多时候都会犯,比如,误以为自己朋友圈中流行的事物就是现在的主流趋势,但很显然任何一个人的社交圈都不足以代表整个社会的主流趋势。
发表性偏见
肯定性的研究发现相比否定性的研究发现更容易发表,而这种现象会影响我们对于事实的判断。
也就是说,媒体对于研究发现的报道是存在偏见的,而这种偏见从根本上讲并非媒体有意而为,很多时候也是因为媒体终究要迎合大众的口味喜好。
人们总是对于反常的、小概率的、出人意料的事件比较感兴趣。同时,大众往往对于那些斩钉截铁、能给出确定性答案的报告比较感兴趣,如果你的报告在最后不能给出一个直截了当的结果,那么多数人都会觉得这篇文章毫无意义,哪怕报告本身是十分严谨且具有学术价值的。
比如对于媒体来说,报道一篇电子游戏与直肠癌有关的研究报告显然要比报道一篇电子游戏与直肠癌无关的报告会获得更多的点击量。前者是勾起大众兴趣的兴奋剂,而后者则是看一眼就觉得毫无新意的陈词滥调。
而对于治疗一些疑难杂症的治疗方法来说,显然发表这种病能被治愈的报道会比发表它们不能被治愈的报道,更具吸引注意力。
就像大家在雪球看股票分析,很多人看了半天最想知道的就是涨不涨,至于别的他并不关心。
举个生活中的例子,在你的印象中,你觉得所有涉及车祸的男女司机中,男女司机的比例大概有多少?想一秒钟。你可能会回答1:2或者是2:1。这个问题对于大多数人来说,答案基本上就是2:1。
因为很多人意识到男司机比女司机要多,所以会觉得男司机应该是2,女司机是1。但是现实生活中的数字远远比这个大,有一组数据显示是4.6:1,男司机是4.6个,女司机是1个。
为什么会这样呢?其实一个重要原因就是因为我们媒体的各种报道。媒体特别喜欢报道女司机出车祸,然后就导致女司机出车祸这个事情在你脑子里面比较容易想起来。报道的比例是什么样的呢?每报道1个男司机出车祸,大概会报道3.8个女司机出车祸。
虽然男司机出车祸的人数远远比女司机多,但报道的比例完全是反过来的。而这些报道的偏见又恰好影响了你对于事件的判断,这就是发表性偏见所造成的误导。
记忆性偏见
马克思主义曾经解释说:人的本质是一切社会关系的总和。假如一个人没有记忆,那么他的社会关系从何而来呢?如果没有记忆,你究竟是谁呢?
记忆很神奇,但并不十分可靠。1993年,一位哈佛大学的研究人员进行了一项关于饮食习惯和癌症关系的研究,他收集了两组女性的饮食习惯数据,一组对象为被诊断出患有乳腺癌的女性,另一组对象则由年龄相仿的健康女性组成,通过对她们早年的饮食习惯进行对比研究发现:患有乳腺癌的女性在年轻时喜欢吃高脂肪含量食物的人数明显偏多。
但实际上,这项研究并不能揭示饮食习惯和癌症之间的关系,仅仅只是告诉我们癌症是如何影响一个女人对她早期饮食习惯的记忆的。所有参与研究的女性在几年前都接受了一个关于饮食习惯的调查,那时她们中间还没有一个人被诊断出患有癌症。一个令人震惊的发现是,患有乳腺癌的女性在回忆她们的饮食构成时,食物的脂肪含量明显上升了,甚至比她实际摄入的要高得多;而没有患上乳腺癌的女性则没有这一倾向。
俗话说:好记性不如烂笔头。也许正是帮我们克服回忆性偏见的好方法。我们很容易将事物进行关联,找出规律,而并非实事求是的进行回忆。人会合理化自己的行为,会试图找出事物的成因,而不能接受毫无理由的事情。
所以当我们明确知道不好的结果后,我们就容易去回忆自己不好的习惯,这样的关联虽然不能帮助我们摆脱现实的困境,但却可以给自己一个看似合理的解释。
幸存者偏见
可以说这是最容易欺骗我们的一种偏见,同时它在金融市场出现的频率十分之高。
有一个案例就很好的解释了这一偏见。在二战时期,美军对德国和日本法西斯展开了大规模战略轰炸,每天都有上千架轰炸机呼啸而去,返回时往往损失惨重。美国空军对此十分头疼:如果要降低损失,就要往飞机上加防弹钢板;但如果整个飞机都加上钢板,那么速度、航程、载弹量等都要受影响。
怎么办?空军请来数学家亚伯拉罕·沃尔德。沃尔德的方法十分简单:他把统计表发给地勤技师,让他们把飞机上弹洞的位置报上来,然后自己铺开一张大白纸,画出飞机的轮廓,再把那些小窟窿一个个添上去。画完之后大家一看,飞机浑身上下都是窟窿,只有飞行员座舱和尾翼两个地方几乎是空白。但到这里并没有结束,问题的关键才刚刚浮出水面。
沃尔德告诉大家:从数学家的眼光来看,这张图明显不符合概率分布的规律,而明显违反规律的地方往往就是问题的关键。飞行员们一看就明白了:如果座舱中弹,飞行员就完了;尾翼中弹,飞机失去平衡就要坠落——这两处中弹,轰炸机多半就回不来了,难怪统计数据是一片空白。因此,结论很简单:只需要给这两个部位焊上钢板就行了。
常规的思维很容易让我们去关注那些窟窿最多的地方,然后对其进行加固处理。而然事实却并非如此,这些能够被我们进行统计的飞机都已经是战争的幸存者了,所以如果不能打破常规思维的局限,破除偏见。我们是无法找到真相的。
在金融市场中,这类情况更为常见,也更为“阴险”。比如基金,那些号称连续跑赢市场大盘的基金,很可能就是这样的一种“幸存者”。
举个例子,假设一家基金公司开放了20只新基金,其中每只基金跑赢大盘的概率都约为50%(这一假设与长期数据是吻合的)。现在,基础概率学告诉我们,该公司第一年只有10只新基金的表现能够打败大盘,连续两年打败大盘的基金为5只,连续3年的基金只剩下了2~3只。
而就在此时,神奇的事情发生了。我们可以对外宣传这2~3只基金,号称它们连续三年跑赢大盘。而然这就像在3次抛硬币中都得到了正面向上的结果,接下来的结果更有可能是回归平均值。
健康用户偏见
定期服用维生素的人更有可能不受疾病困扰,原因往往不是维生素有什么特殊功效,而是因为他们就是那类定期服用维生素的人。
《纽约时报》健康专栏作家加里·陶布斯对此进行过解释:“就从最简单的角度来分析,那些忠于健康生活方式的人(按时吃药、定期运动、饮食规律等)与其他人有本质区别,这就是问题所在。”
对于那些试图揭示某些活动(如定期运动或规律饮食等)是否对健康有益的研究来说,这样的一种偏见可能会使结论变得没有那么清晰。我们觉得自己所比较的只是某种单一的饮食差异或生活习惯,但事实上,如果处理组和控制组的成员没有实现完全的随机取样,我们所比较的就是两类不同的人了:习惯规律饮食的那一组人拥有健康的生活习惯,而不习惯的人可能在生活的其他方面也忽略健康习惯。
就像能够保持定期运动的人,不仅仅是在运动方面与别人有差异,同时也意味着他们的生活有着基本的保证,有着稳定可靠的收入来源以及众多其它因素。所以你会发现,本来你想证明的是运动与人的健康关系,但很可能你收集到的证据是在说明生活收入越稳定且越高的人越健康。
那么,面对上述五种偏见我们应该怎么做呢?或者说我们应该如何识破上述五种偏见呢?
核心在于我们要清楚一个事实,就是我一开始讲的:相关关系并不等于因果关系。
两个变量存在正相关或负相关的关系,这并不代表其中一个变量的改变是由另一个变量的变化引起的。
就像前面所说的运动与健康的例子,运动的人多数都很健康,这并不能证明运动就能使人健康,更不能说明健康的原因是运动。因为这其中还会有影响事物的第三因素。
比如书中的一个例子,在美国有一项统计数据显示:学生的考试成绩和家里拥有的电视机数量呈正相关。但这并不意味着望子成龙的家长多买电视机,孩子的成绩就能提高。
合理的解释是:受过良好教育且收入稳定的家庭既能够买的起多台电视机,也能辅导好孩子的学习,使其在考试中发挥出色。在这其中,电视机数量很可能是由第三变量(家长的受教育程度或者家庭收入)来决定的。
错误的把相关关系当做因果关系来看,就会让我们被那些隐藏的第三变量所迷惑,从而忽视掉事物的真正起因。同时,它还会让我们出现因果倒置的错觉。
最后,祝水手们中秋节愉快!

