
导语

熊巍 | 作者

论文题目: Koopman neural operator as a mesh-free solver of non-linear partial differential equations 论文链接: https://doi.org/10.1016/j.jcp.2024.113194 KoopmanLab的论文: https://doi.org/10.1063/5.0157763 KoopmanLab的代码: https://github.com/Koopman-Laboratory/KoopmanLab
1. 背景
1. 背景
2. Koopman 理论和动力系统视角下的
偏微分方程求解问题
2. Koopman 理论和动力系统视角下的
偏微分方程求解问题
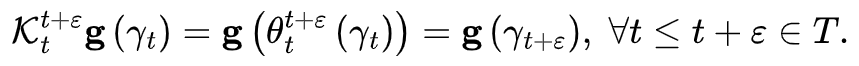
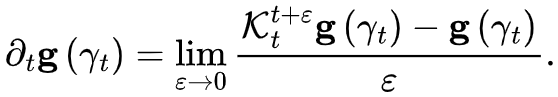
3. Koopman神经算子
3. Koopman神经算子
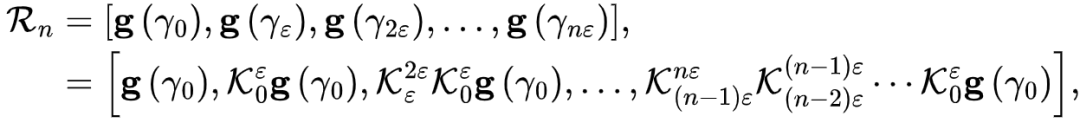
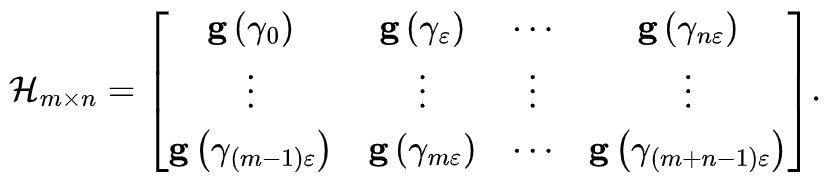

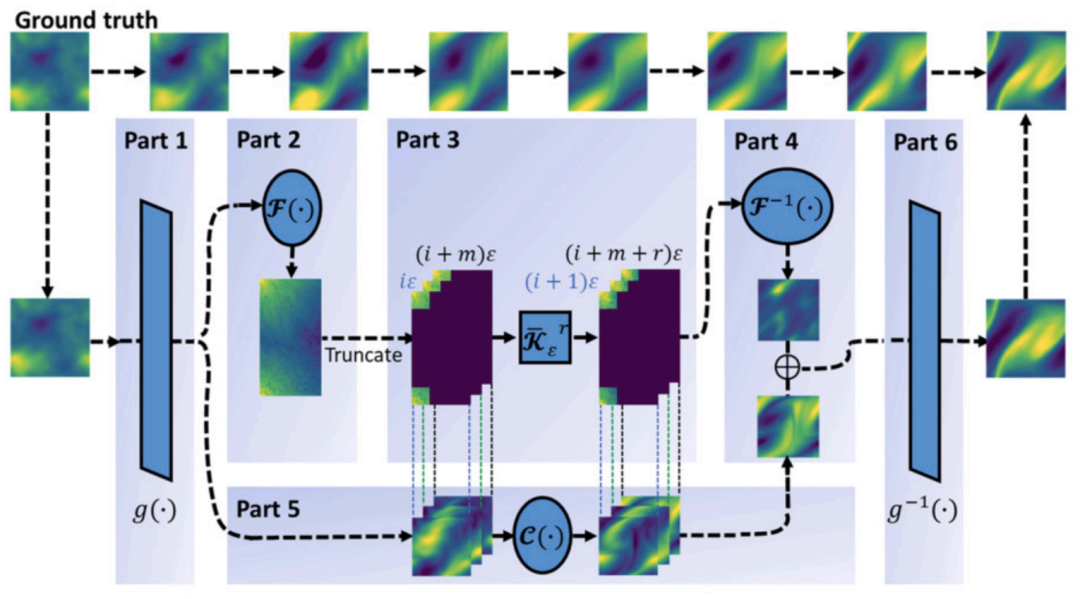
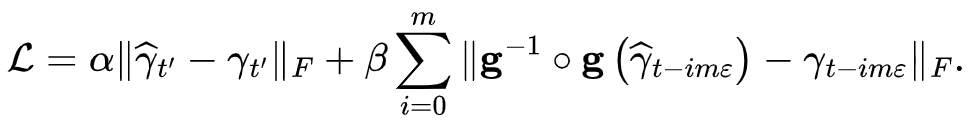
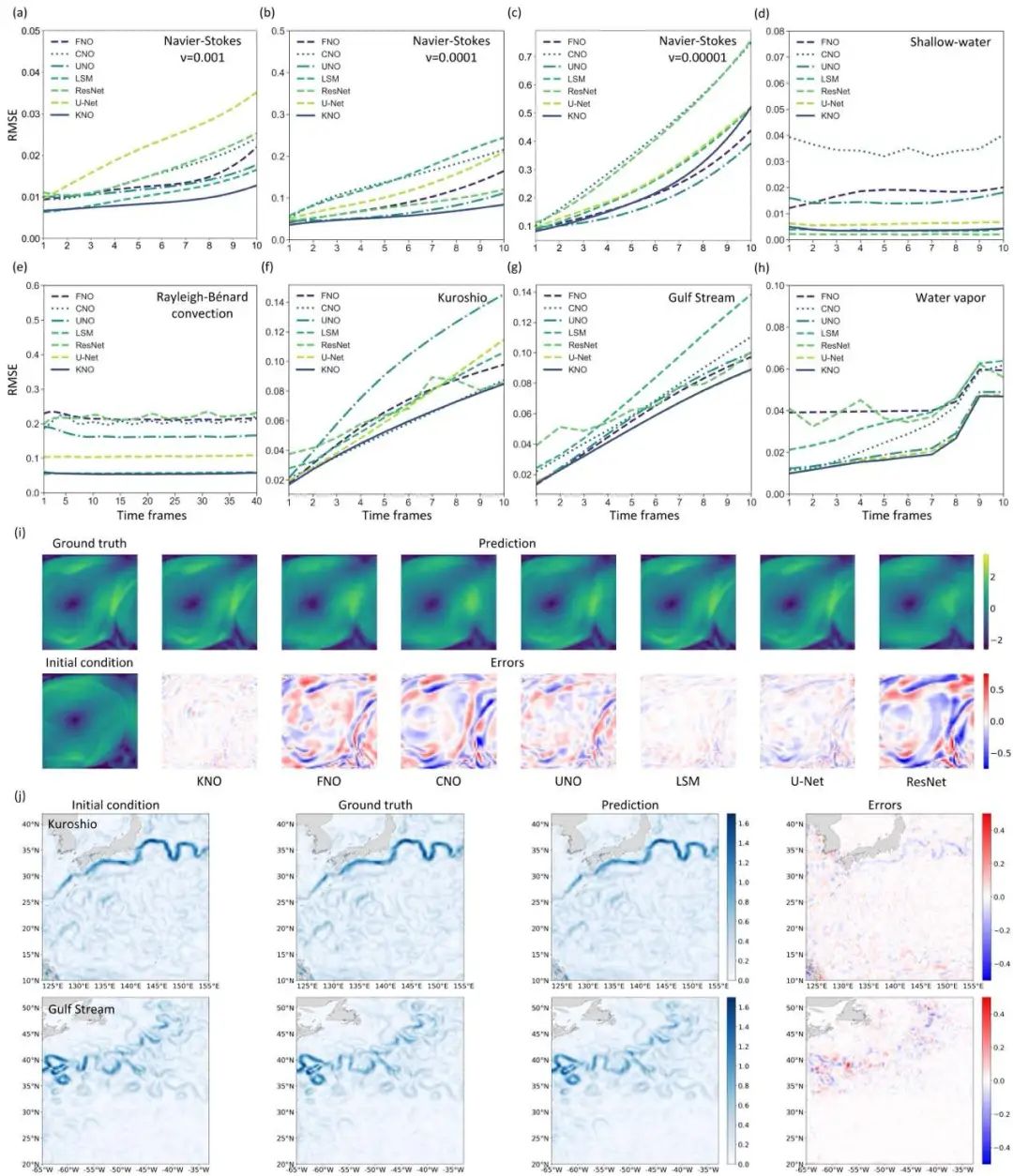
4. Koopman神经算子的性质
4. Koopman神经算子的性质
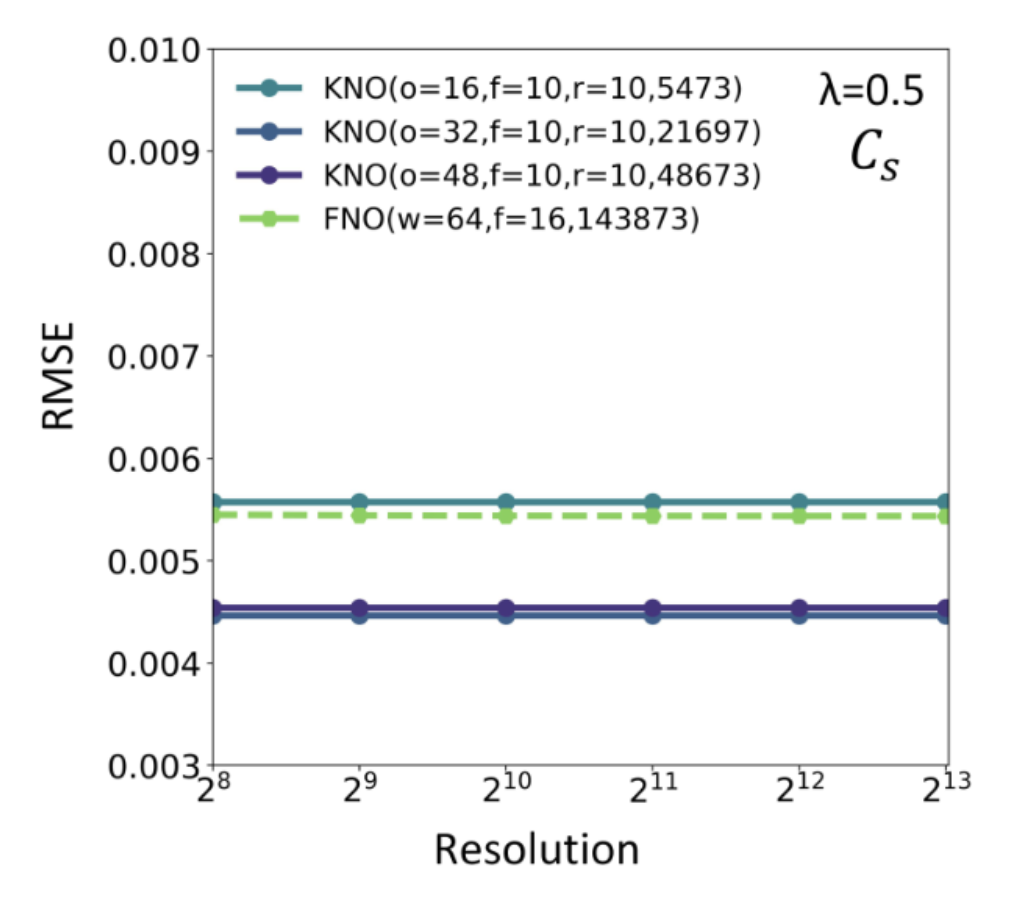
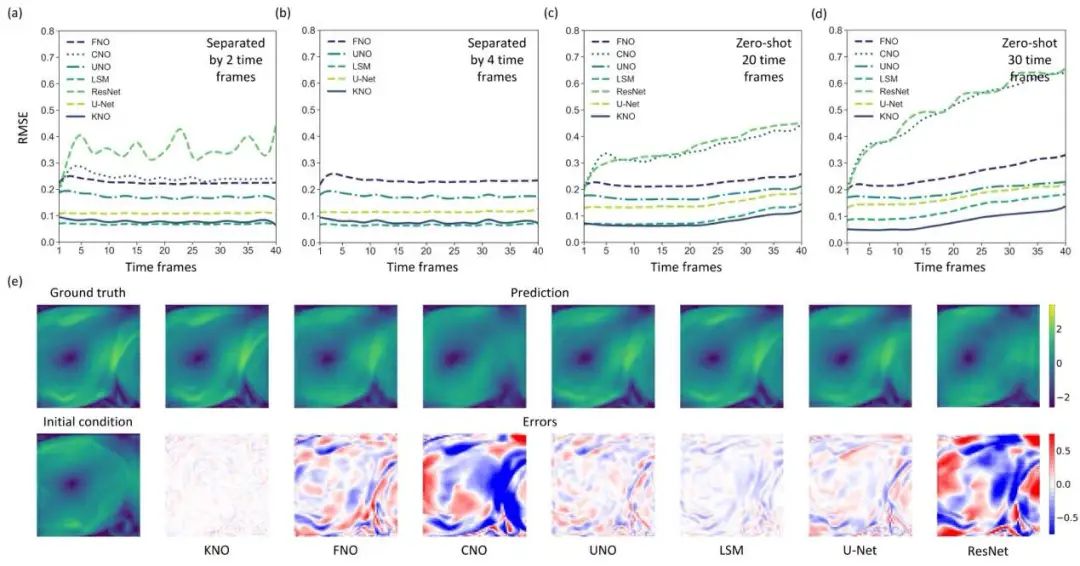
5. 总结
5. 总结

AI By Complexity读书会
大模型、多模态、多智能体层出不穷,各种各样的神经网络变体在AI大舞台各显身手。复杂系统领域对于涌现、层级、鲁棒性、非线性、演化等问题的探索也在持续推进。而优秀的AI系统、创新性的神经网络,往往在一定程度上具备优秀复杂系统的特征。因此,发展中的复杂系统理论方法如何指导未来AI的设计,正在成为备受关注的问题。
集智俱乐部联合加利福尼亚大学圣迭戈分校助理教授尤亦庄、北京师范大学副教授刘宇、北京师范大学系统科学学院在读博士张章、牟牧云和在读硕士杨明哲、清华大学在读博士田洋共同发起「AI By Complexity」读书会,探究如何度量复杂系统的“好坏”?如何理解复杂系统的机制?这些理解是否可以启发我们设计更好的AI模型?在本质上帮助我们设计更好的AI系统。读书会于6月10日开始,每周一晚上20:00-22:00举办。欢迎从事相关领域研究、对AI+Complexity感兴趣的朋友们报名读书会交流!
6. 加入集智,一起复杂!
点击“阅读原文”,报名读书会


