今天为大家介绍的是来自清华大学的张颢团队的一篇论文。近年来，分子生成算法在药物设计中的应用迅速发展，而分子多样性是分子生成算法性能的一个重要方面。然而，现有的指标，例如richness和internal diversity，无法有效地度量分子多样性，因为它们无法同时反映分子多样性的两个方面：分子数量和分子不相似性。针对这一挑战，作者提出了Hamiltonian diversity（哈密顿多样性），定义为分子集合中的最短哈密顿环。这种新指标从理论上同时反映了分子多样性的两个方面。作者提供了Hamiltonian diversity的高效Python实现，并且展示了它与真实世界分子多样性的高度一致性和它在分子生成算法设计中的应用潜力。

药物研发是一个多阶段的“漏斗式”筛选过程，因此药学家们期望在上游的药物分子设计阶段得到尽可能多样的候选分子集合，从而提高最终实现药物上市的概率。此外，多样的药物分子也有利于缓解耐药性和副作用等。因此，对于分子生成方法，其生成分子的多样性是算法评估中的一个核心指标。

在计算机辅助药物设计中，richness和internal diversity (IntDiv) 是最常用的两种分子多样性指标。其中，richness定义为分子集合的大小，反映了“分子数量”，而IntDiv定义为分子集合中两两距离的平均值，反映了“分子不相似性”。如下图所示，这两个指标反映了分子多样性两个正交的方面，因此在比较两个分子集合的多样性时可能得到不同的结果，导致争议。

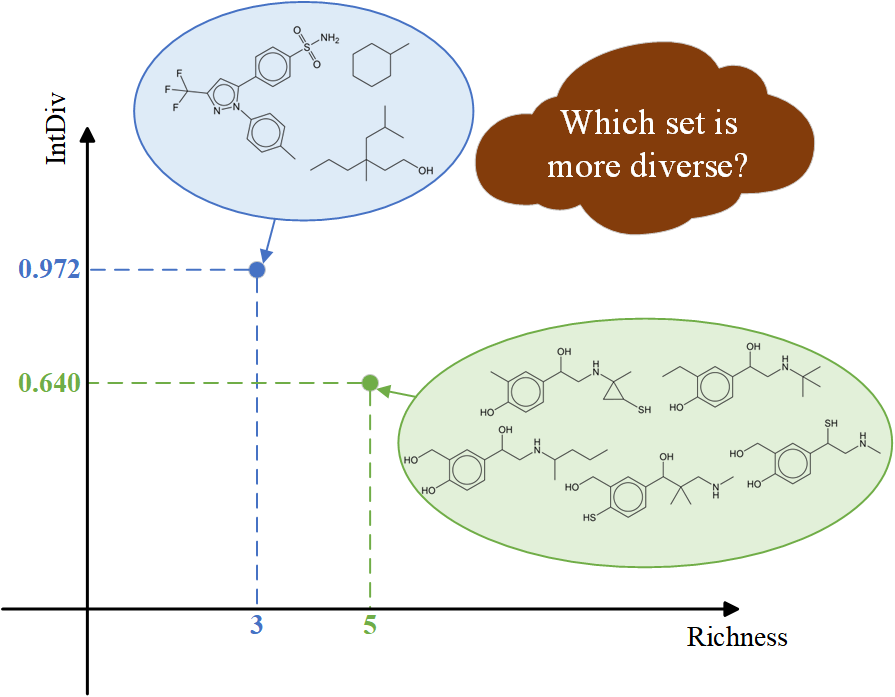
作者首先系统地回顾了现有的分子多样性指标，并将其分为两类：以richness为代表的reference-based指标和以IntDiv为代表的distance-based指标。作者进而提出，理想的分子多样性指标应当满足两个原则：

单调性：

在分子集合中加入一个新分子，其多样性不减，且当且仅当新分子与已有分子之间距离为0时多样性不变；

不相似性：

对于两个两分子集合，分子距离较大的集合分子多样性也较大。

作者指出，现有的分子多样性指标都不能同时满足这两个原则。

为解决上述问题，作者提出将分子集合直观地对应于一个无向完全图，其中每个顶点表示一个分子，每条边的权重为两分子之间的距离。哈密顿环是图论中的重要概念，即一条经过图中每个顶点有且仅有一次的环路，而最短哈密顿环的求解即图论中经典的旅行商问题（TSP）。Hamiltonian Diversity（HamDiv）定义为分子集合对应的图中的最短哈密顿环。

作者从理论上验证了HamDiv同时满足单调性和不相似性两个原则，其中单调性由分子距离度量的三角不等式保证。目前最常用的分子距离指标是扩展连通性指纹（ECFPs）之间的谷本距离（Tanimoto distance），它满足三角不等式，也被用于IntDiv等现有指标的计算中。因此，在HamDiv的实现和定量实验中都使用了这一距离指标。

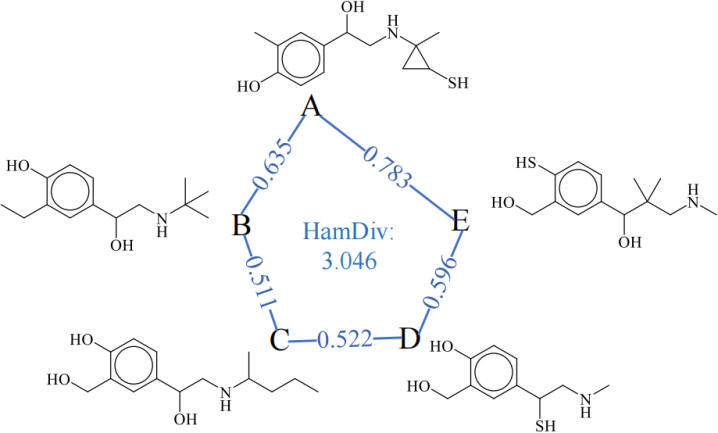
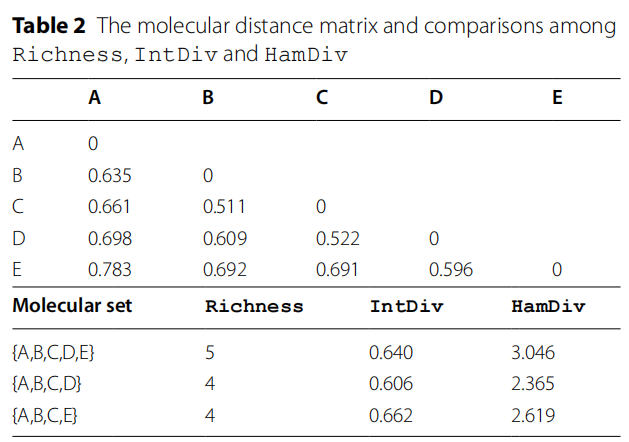
上图给出了一个分子集合的实例。结果表明，richness不满足不相似性原则，IntDiv不满足单调性原则，而HamDiv同时满足两个原则。此外，它还具有较强的可解释性，即每个分子对多样性的贡献可以被定量表示。

HamDiv的求解过程TSP是一个NP-hard问题。作者对比了TSP不同的精确和近似求解方法的速度和精确度，并针对不同大小的分子集合选用不同的方法，使得HamDiv的求解对10000个分子以内的集合计算可行。

在实验部分中，作者选用生物活性数据集作为分子多样性的金标准，对比了不同分子多样性指标与金标准的相关系数。结果表明，与已有的其他指标相比，HamDiv与真实世界分子多样性具有更高的一致性。此外，作者将HamDiv融合到了Reinvent分子生成算法的损失函数中，有效提升了算法生成分子的多样性，这表明HamDiv可以为分子生成算法的设计提供指导。

总而言之，HamDiv是首个同时满足两个分子多样性原则的指标，这对于公平有效地评估分子多样性至关重要。目前，大部分分子生成算法的评估方式是，在生成的分子中选取固定数目（例如100个）最高分分子，对比其性质得分的均值和IntDiv。虽然Richness的固定保证了IntDiv对比的公平性，但是性质得分和IntDiv之间仍然存在trade-off，导致对比结果的争议。基于HamDiv，研究者可以设定一个性质得分的固定阈值，并计算算法生成的超过阈值的分子集合的HamDiv，从而公平地对比分子多样性。

Hu, X., Liu, G., Yao, Q. et al. Hamiltonian diversity: effectively measuring molecular diversity by shortest Hamiltonian circuits. J Cheminform 16, 94 (2024). 

https://doi.org/10.1186/s13321-024-00883-4