文章认为宇宙在初始时的低熵状态是输入数据，随着时间推移，熵增加直至宇宙热寂，这是加密机器的输出。物理定律是加密算法，量子层面的随机性是加密密钥。我们虽能观察输入和输出，但因不知密钥而无法预测未来。

为理解加密宇宙的运作，需考虑两层现实模型。模拟层是我们能观察和互动的现实，受我们所知的物理定律支配；底物层是运行宇宙模拟的计算框架，加密过程在此真正运行，密钥也在此，且从模拟现实中不可直接观测。

量子事件是两层之间的独特接口，当量子相互作用发生时，就像模拟瞬间触及底物层以获取加密密钥。该模型解释了非局域性和纠缠，调和了量子力学与狭义相对论，还为测量问题提供了新视角。

在加密宇宙模型中，不确定性原理代表了在量子层面的持续重新加密过程。每次量子测量可视为一个小型加密事件，该机制确保在任何给定时间从系统中可提取的总精确信息是有限的。

Published on August 14, 2024 1:21 PM GMT

Epistemic status: Fun speculation. I'm a dilettante in physics and encryption so some mistakes might be expected.

The metaphysical claim:

Imagine an external universe that seeks to encrypt or hash an enormous amount of data to defend against a powerful adversary. For this purpose, it has built an extremely sophisticated and self-contained encryption machine. I suggest that our universe is this encryption machine, which is being simulated by the external world.

Note: Let's leave the encryption vs hashing an open question for now. When discussing encryption, take into account it might also be hashing.

The Encryption Universe Model

Mechanism:

Consider the universe at its inception — perhaps described by the universal Schrödinger equation — as the input data our external universe aims to encrypt or hash. Due to the second law of thermodynamics, the universe must have started in a low entropy state. With time, entropy increases until the universe's heat death, where the entropy reaches maximum. This final state will be the output of the encryption machine that is our universe.

Let's consider the process and map it to the different parts of encryption algorithms:

Input: Low entropy state in the Big Bang, which is correlated to the information we desire to encryptProcess: Laws of physics - the encryption algorithm that scrambles the physical waves/particles in a way to maximize the entropy in a complex mannerEncryption key: A hidden input that randomizes the result of the encryption process. In our case, this is exactly the randomness we see at the quantum level and the reason for the existence of the uncertainty principleOutput: The maximum entropy state at the heat death of the universe

The view from inside an encryption machine

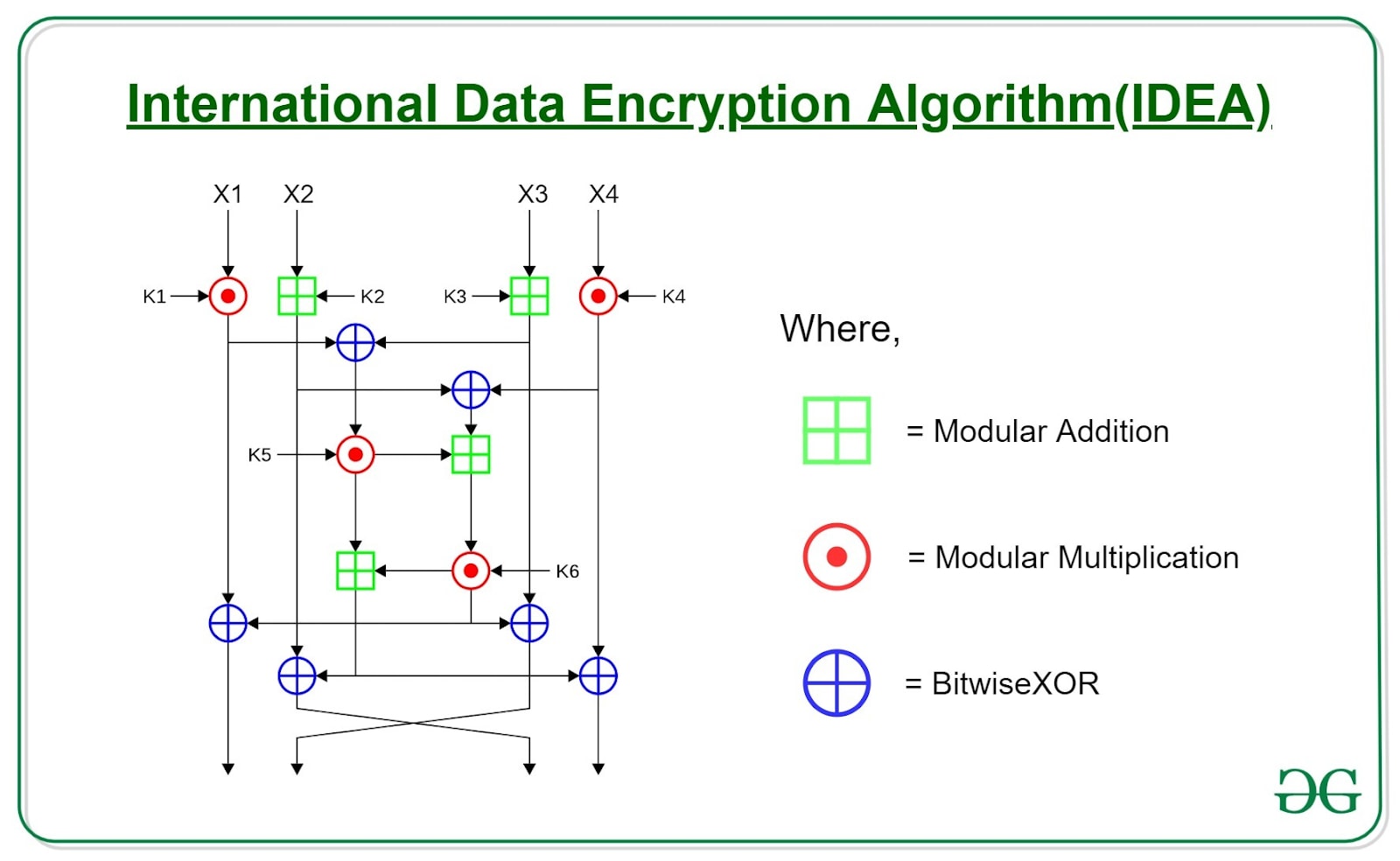
Imagine you live inside a very simple encryption machine, for example, a machine that implements the IDEA algorithm. Let's say that you are privileged to see the input at each step and the output of each step, but you don't see the key. In our universe, the input is the world's configuration at time t, and the output is its configuration at time t+1

With enough observation and deductive ability, you would be able to draw this chart from within the machine. You could even deduce the key while looking at the past, but you will still never be able to predict the future because you don't have the encryption key. You have only seen the part of it that has already been used, but without knowing the entire key, you could never predict the future. Does that sound familiar?

In the following sections, we'll explore how this model explains various quantum phenomena, addresses the relationship between quantum mechanics and relativity, and even sheds light on the nature of life in our universe.

The Two-Layer Reality

To understand how our encryption universe operates, we need to consider a two-layer model of reality. Let's use our IDEA encryption machine analogy to make this concept more tangible.

Simulated layer (our observable universe)

This is the reality we experience and observe. It's analogous to the internal state of the IDEA encryption machine that we, as hypothetical inhabitants, can see and interact with. In our universe, this layer is governed by the laws of physics as we know them.

In the IDEA machine analogy:

This would be like seeing the input at each step and the output of each step of the encryption process.You can observe how data changes from one state to another, but you can't see why it changes in that specific way.

Substrate layer (the "hardware" running the simulation)

Beneath the simulated layer lies the substrate - the computational framework that runs our universe-simulation. This is where the encryption process truly operates, and where the encryption key resides. The substrate layer is not directly observable from within our simulated reality.

In the IDEA machine analogy:

This would be the actual mechanism of the IDEA algorithm, including the parts we can't see - most crucially, the encryption key.It's the "black box" that determines how the input is transformed into the output at each step.

How quantum interactions access the substrate layer

Quantum events represent a unique interface between these two layers. When a quantum interaction occurs, it's as if the simulation is momentarily reaching down into the substrate layer to access the encryption key.

In the IDEA machine analogy:

This would be like the moments when the machine applies the key to transform the data.We can't see this process directly, but we see its effects in how the observable state changes.

The implications of this two-layer reality for quantum mechanics, relativity, and other physical phenomena will be explored in subsequent sections.

Resolving Paradoxes

Now that we've established our two-layer model of reality, let's see how it helps us tackle some of the most perplexing paradoxes in modern physics.

Non-locality and entanglement explained

This model explains non-locality in a straightforward manner. The entangled particles rely on the same bit of the encryption key, so when measurement occurs, the simulation of the universe updates immediately because the entangled particles rely on the same part of the secret key. As the universe is simulated, the speed of light limitation doesn't play any role in this process.

In other words, what appears to us as "spooky action at a distance" is simply the instantaneous update of the simulation based on the shared encryption key bit. There's no actual information traveling faster than light within our simulated reality - the update happens at the substrate level, outside the constraints of our spacetime.

Reconciling quantum mechanics with special relativity

The apparent conflict between quantum non-locality and special relativity finds a natural resolution in our encryption universe model. Here's how:

Special relativity operates within the simulated layer of our universe. It's a rule of the simulation, limiting the speed of information propagation within our observable reality.Quantum non-locality, on the other hand, operates at the substrate level. When quantum interactions occur, they're accessing the encryption key in the substrate, bypassing the rules of the simulated layer.From our perspective within the simulation, it looks like quantum effects violate special relativity. But there's no real contradiction because these effects aren't actually propagating through our spacetime - they're happening "outside" of it, in the substrate.

This reconciliation doesn't require us to modify either quantum mechanics or special relativity. Instead, it provides a framework where both can coexist, operating at different levels of reality.

The measurement problem revisited

The measurement problem in quantum mechanics asks why we observe definite outcomes when we measure quantum systems, given that the wave function describes a superposition of possible states. Our encryption universe model offers a fresh perspective on this:

Before measurement, the wave function represents all possible states, much like how an encryption algorithm can produce many possible outputs depending on the key.The act of measurement is analogous to the application of a specific part of the encryption key. It's the moment when the simulation accesses the substrate to determine the outcome.The "collapse" of the wave function isn't a physical process within our simulated reality. Instead, it's the point where the simulation resolves the quantum superposition by applying the relevant part of the encryption key.The apparent randomness of the outcome is a result of our inability to access or predict the encryption key, not a fundamental property of nature itself.

This view of measurement doesn't require any additional mechanisms like consciousness-induced collapse or many-worlds interpretations. It's simply the interface between the simulated layer we inhabit and the substrate layer where the "computation" of our universe occurs.

In the taxonomy of quantum theories, this model falls under non-local hidden variable theories, but with a unique twist: the "hidden variables" (our encryption key) act non-locally at a more fundamental level of reality, outside our simulated spacetime.

The Uncertainty Principle: Continuous Re-encryption

In our encryption universe model, the uncertainty principle takes on a new significance. Rather than a static security feature, it represents a process of continuous re-encryption at the quantum level.

Each quantum measurement can be viewed as a mini-encryption event. When we measure a particle's position precisely, we've essentially "used up" part of the local encryption key. Immediately attempting to measure its momentum applies a new portion of the key, disturbing our previous position measurement. This isn't just about measurement disturbance - it's a fundamental limit on information extraction.

This mechanism ensures that the total precise information extractable from the system at any given time is limited. It's as if the universe is constantly refreshing its encryption, preventing any observer from fully decrypting its state.

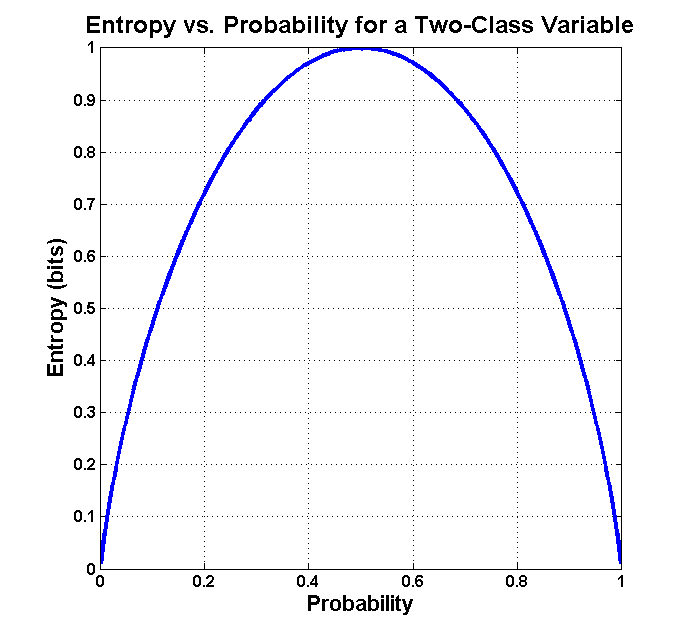
The symmetrical nature of many quantum probabilities (often close to 50-50 chances) aligns with maximizing entropy in these mini-encryption events. As shown in the entropy vs. probability graph for a two-class variable, entropy peaks at equal probabilities, providing minimal information about the underlying system - exactly what an effective encryption process aims for.

By framing these paradoxes within the context of our encryption universe model, we can see how seemingly irreconcilable aspects of quantum mechanics and relativity can coexist. Of course, this model raises its own set of questions and challenges, which we'll address in later sections.

Implications for Classical Physics

Our encryption universe model doesn't just explain some quantum phenomena - it also has interesting implications for classical physics and the nature of our reality at larger scales.

The role of entropy in the encryption process

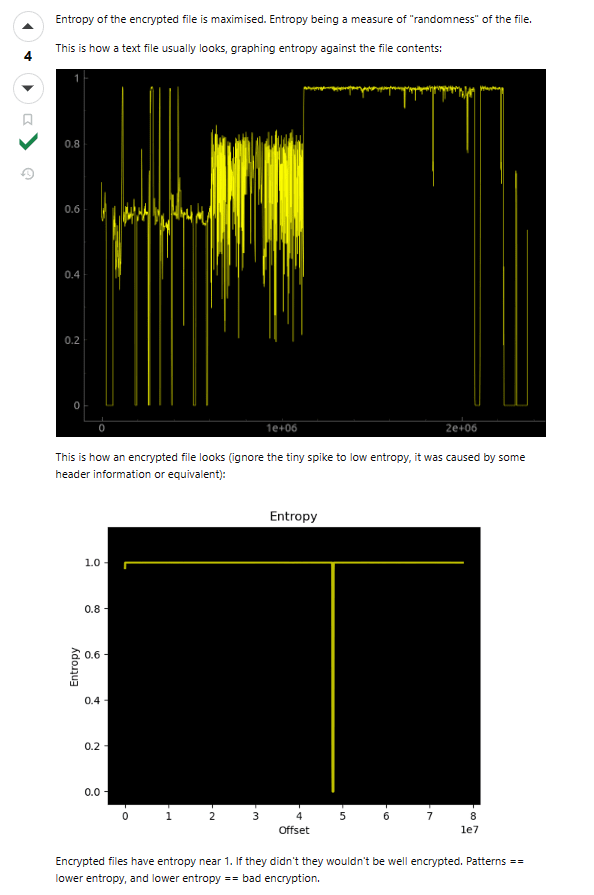
Every efficient encryption algorithm maximizes entropy of the output, because maximum entropy provides minimal information about the content. For example, both random strings (zero information) and encrypted files have maximum entropy.

And this is exactly what the laws of physics create with time. The entropy of the universe is only increasing to reach maximum entropy in the heat death of the universe. In our model, this isn't just a quirk of thermodynamics - it's a fundamental feature of the encryption process that underlies our reality.

The second law of thermodynamics, then, can be seen as a direct consequence of our universe being an encryption machine. As the encryption process runs its course, it's constantly working to maximize entropy, scrambling the initial low-entropy state of the universe into an eventual state of maximum entropy.

Speed of light as a computational optimization

So, outside of quantum-level non-locality, it seems that all other interactions are limited to the speed of light. Considering this theory, the explanation is that the rules of physics in every scale above the quantum scale are meant to create additional complexity to make it harder to reverse compute the encryption algorithm. It's the same purpose that the modular addition, modular multiplication, and XOR combinations play in the IDEA algorithm compared to using something more trivial like a keyed Caesar cipher.

However the price that is paid for this complexity is a higher computational cost. The speed of light in this context is meant to optimize the tradeoff between computational cost and complexity. Without the speed of light limitation, the computational cost of the simulation would increase significantly due to the added computations because of the increase in the size of the light cone, thus increasing the amount of matter that is causally connected and has to be computed as well.

The only non-locality happens in the quantum level because the interactions are being computed directly against the private key due to security reasons and necessity to preserve uncertainty, while in non-quantum interactions, determinism is acceptable.

Life and complexity in the encryption machine

As we discussed before, the laws of the universe are built to scramble the initial setup of the universe by dissipating heat (free energy) and thus maximizing entropy. If we think of life as a feature of our universe/encryption machine, it serves two roles:

Accelerating the increase in entropy in the universe: For surviving, keeping homeostasis, and reproducing, life forms must find pockets of free energy to consume, thus burning them more quickly compared to the case where life didn't exist.Increasing the complexity of the interactions: Interactions that involve complex arrangements of material like life forms create more computationally complex and chaotic outcomes compared to large but simple entropy maximization machines like stars or black holes. Consider, for example, the process by a low entropy photon radiating from the sun, absorbed by a plant, eaten by a herbivore, then eaten by a predator, and then turned into infrared radiation (thus preserving the energy but increasing the entropy) passes. This is a much more complex encryption route compared to being absorbed by a black hole and later radiated as Hawking radiation.

This is again similar to the extra computation steps that we use in encryption algorithms compared to simplistic permutations. By the same logic, life increases computation costs significantly, and we might be worried our simulators might turn the encryption machine off if life starts to become the prevalent entropy-maximizing force in the universe compared to inanimate objects. But it also might be that this is something that was planned, and thus the speed of light limitation is something that was specifically calculated to account for a universe filled with life.

In this view, life isn't just a quirk of chemistry but an integral part of the encryption process - a particularly effective means of increasing entropy and computational complexity in our simulated universe.

Challenges and Objections

Speculative Nature and Compelling Aspects This theory, while speculative, offers a unified logical explanation for various physical laws from a functional perspective. It addresses the second law of thermodynamics, quantum randomness, the uncertainty principle, the speed of light limitation, and quantum non-locality. No other metaphysical theory provides justification for this specific architecture of the universe.Scientific Refutability Contrary to initial impressions, this theory can be refuted. Discoveries that could disprove it include:
Cracking quantum randomness (predicting the encryption key)Observing a decrease in the universe's entropyAny new physical discovery incompatible with the universe functioning as an encryption machine
Occam's Razor Consideration While this theory adds complexity by proposing an external universe and encryption process, it unifies seemingly unrelated physical phenomena. The trade-off between initial complexity and explanatory power makes it challenging to definitively assess whether it violates Occam's Razor.Historical Context and Technological Bias A valid criticism is that this theory might fall into the trap of describing the universe using current technological paradigms, similar to how clockwork mechanisms or hydraulic systems influenced past theories. However, this model offers more than a trendy metaphor:
It provides explanations for puzzling aspects of physics in a unified frameworkIt uses well-established principles of information theory and thermodynamicsIt makes non-obvious connections, such as linking entropy maximization in encryption to universal behavior
Lack of Direct Testability A significant limitation is the theory's lack of direct testability, a weakness from a scientific standpoint. However, this challenge isn't unique to our model; other metaphysical interpretations of quantum mechanics face similar issues (Like the popular Many-worlds interpretation). While this limits strict scientific validity, such interpretations can still:
Provide value through explanatory power and conceptual coherenceInspire new avenues of thought or researchOffer alternative perspectives for understanding quantum phenomena

Look at it this way: We've got a universe that starts simple and gets messier over time. We've got particles that seem to communicate instantly across space. We've got quantum measurements that refuse to give us complete information. Now imagine all of that as lines of code in a cosmic encryption program. The entropy increase? That's the algorithm scrambling the initial input. Quantum entanglement? Two particles sharing the same bit of the encryption key. The uncertainty principle? A continuous re-encryption process, limiting how much information we can extract at once.

Is it true? Who knows. But it's a bit like solving a puzzle - even if the picture you end up with isn't real, you might stumble on some interesting patterns along the way. And hey, if nothing else, it's a reminder that the universe is probably a lot weirder than we give it credit for.