近年来，IMO 年度竞赛被广泛认为是机器学习的一大挑战，也是衡量 AI 系统高级数学推理能力的理想基准。

今年，Google DeepMind 将其联合 AI 系统应用于 IMO 组织者提供的问题。他们的解决方案根据 IMO 的评分规则进行了评分，评分者包括著名的数学家、IMO 金牌得主和菲尔兹奖得主 Timothy Gowers 教授，以及两次 IMO 金牌得主、2024 年 IMO 问题选择委员会主席 Joseph Myers 博士。

IMO 金牌得主和菲尔兹奖得主 Timothy Gowers 教授称：“这个程序能提出如此非显而易见的结构，非常令人印象深刻，远远超出了我认为的最先进水平。”

首先，问题被手动翻译成形式数学语言，以便该系统理解。在正式竞赛中，学生有两个 4.5 小时的时段提交答案。该系统在几分钟内解决了一个问题，而解决其他问题则花了最多三天时间。

AlphaProof 通过确定答案并证明其正确性，解决了两个代数问题和一个数论问题。这包括今年 IMO 中只有五个参赛者解决的最难问题。AlphaGeometry 2 证明了几何问题，而两个组合数学问题仍未解决。

每个问题可以赢得七分，总分最高为 42 分。该系统最终得分 28 分，在解决每个问题上都获得了满分——相当于银牌类别的最高端。今年，金牌的门槛从 29 分开始，在正式比赛的 609 名参赛者中有 58 人达到了这个分数。

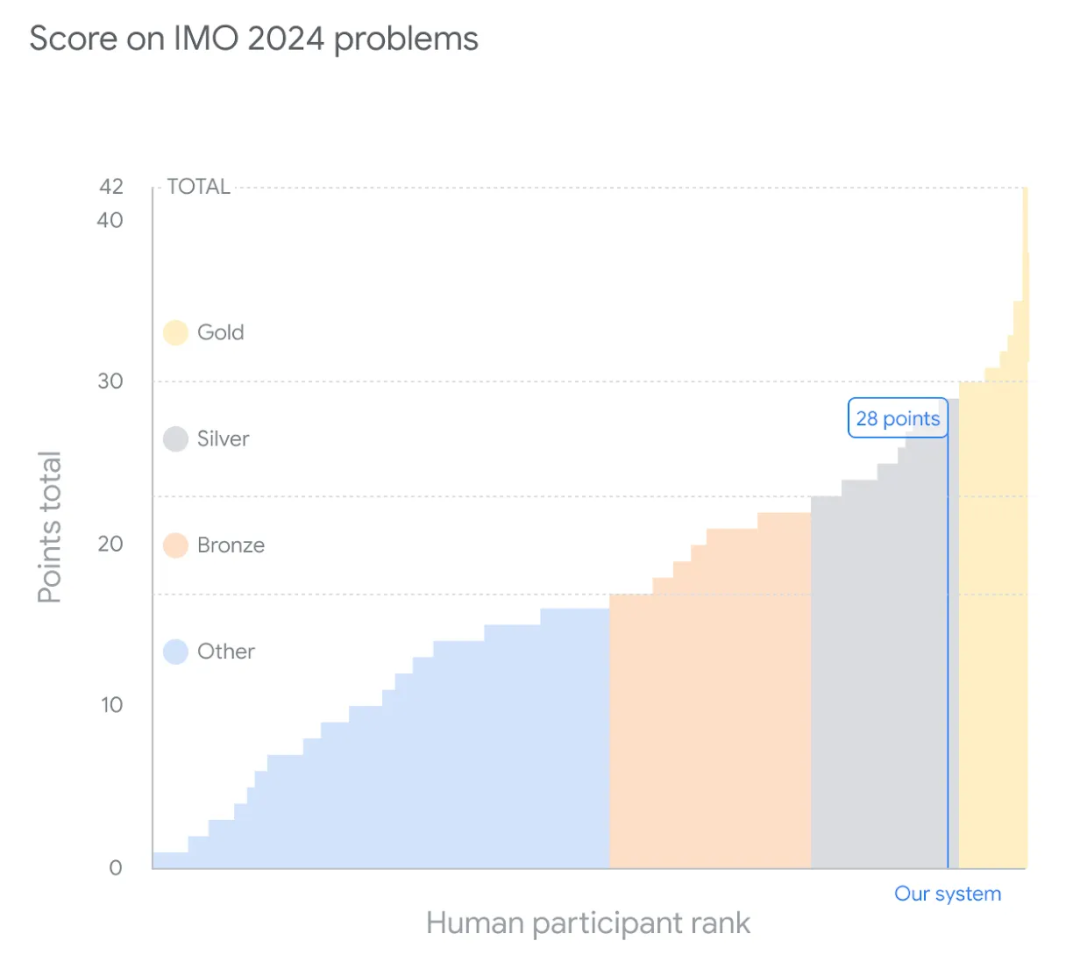
图 | 该人工智能系统在 IMO 2024 上相对于人类竞争者的表现。

AlphaProof 是一个系统，它自我训练以在 Lean 的形式语言中证明数学陈述。它将一个预训练的语言模型与 AlphaZero 强化学习算法相结合，后者之前自学掌握了国际象棋、将棋和围棋的游戏。

形式语言提供了关键优势，即涉及数学推理的证明可以正式验证其正确性。然而，它们在机器学习中的应用之前受到了人类编写数据极其有限的制约。

相比之下，基于自然语言的方法可以在拥有更多数量级数据的情况下，虚构出看似合理但错误的中间推理步骤和解决方案。研究团队通过微调一个 Gemini 模型，自动将自然语言问题陈述翻译成形式陈述，从而在这两个互补的领域之间架起了一座桥梁，创建了一个大型的不同难度的形式问题库。

当 AlphaProof 面对一个问题时，它会生成解决方案候选，然后通过在 Lean 中搜索可能的证明步骤来证明或反驳它们。每个找到并验证的证明都被用来强化 AlphaProof 的语言模型，增强其解决后续更复杂问题的能力。

他们在 IMO 之前通过几周的时间训练 AlphaProof，证明了或反驳了数以百万计的问题，涵盖了各种难度和数学主题领域。训练循环在比赛期间也被应用，强化了自我生成比赛问题变体的证明，直到找到完整的解决方案。

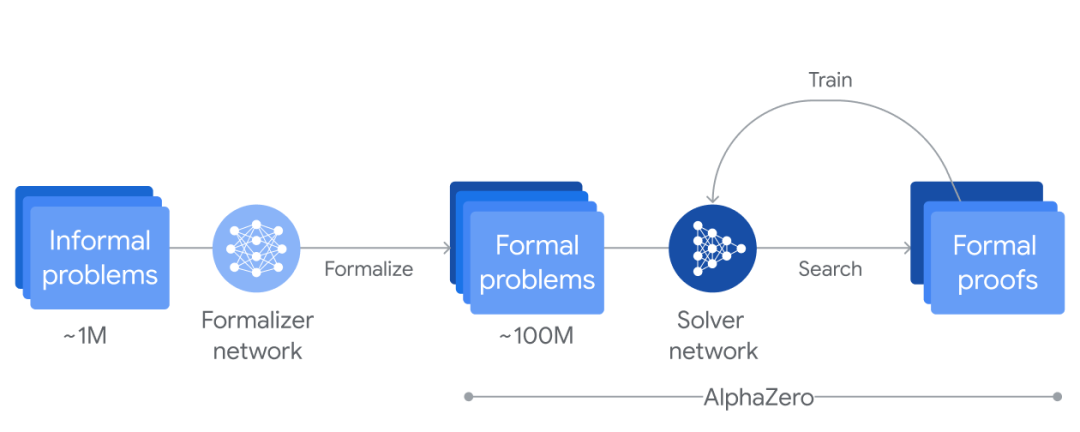
图 | AlphaProof 的强化学习训练循环过程。

AlphaGeometry 2 是 AlphaGeometry 的显著改进版本。它是一个神经符号混合系统，其语言模型基于 Gemini，并在比其前身多一个数量级的合成数据上从头开始训练。这帮助模型解决更具有挑战性的几何问题，包括关于物体运动和角度、比例或距离的方程问题。

AlphaGeometry 2 使用的符号引擎比其前身快两个数量级。面对新问题时，一种新颖的知识共享机制被用来实现不同搜索树的先进组合，以解决更复杂的问题。

在今年的比赛之前，AlphaGeometry 2 能够解决过去 25 年所有历史 IMO 几何问题中的 83%，而其前身的解决率为 53%。对于 2024 年的 IMO，AlphaGeometry 2 在接收到问题的形式化后仅用 19 秒就解决了第 4 题。

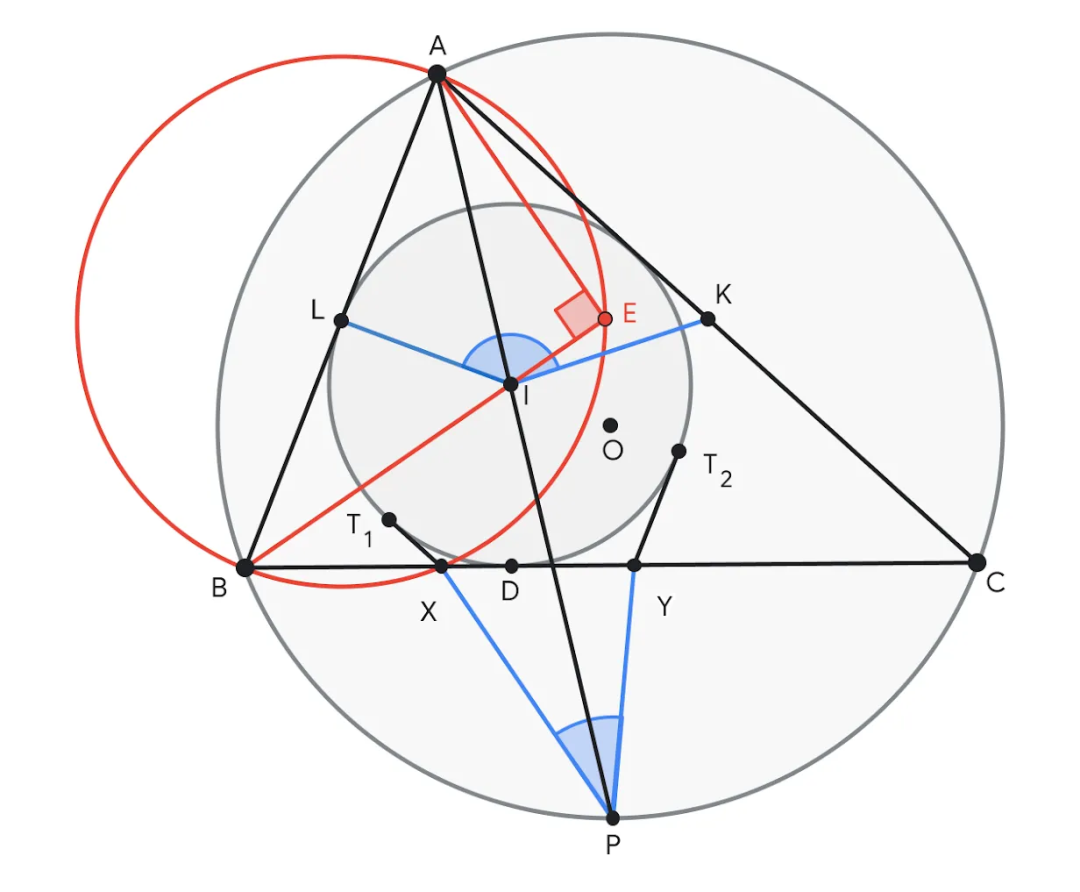
图 | AlphaGeometry 2 提出在直线 BI 上构造点 E，使 ∠AEB = 90°。点 E 有助于给 AB 的中点 L 提供目的，创造了许多对类似的三角形，如 ABE ~ YBI 和 ALE ~ IPC，以证明结论。

此外，研究团队还尝试了一个基于 Gemini 和他们最新研究的自然语言推理系统，以实现高级问题解决技能。这个系统不需要将问题翻译成形式语言，并且可以与其他 AI 系统结合使用。他们今年也用这种方法测试了 IMO 问题，结果显示出巨大的潜力。