摘要

近年来，大规模推理模型在诸多高难度数学基准（如 GSM8K、MATH500、AIME 2024）上取得了最先进的性能，但其内部成功机理仍鲜有解析。本文提出并构建了“推理图”（reasoning graph）——通过对推理过程中隐藏态进行 K-means 聚类，将每一步操作映射为图中的节点，并以节点访问顺序构建有向边，从而刻画模型的推理路径。基于此，我们系统地分析了推理图的三大图论性质：循环结构（cyclicity）、图直径（diameter） 和小世界指数（small-world index）。研究发现，经过蒸馏的推理模型（例如 DeepSeek‑R1‑Distill‑Qwen‑32B）相比基础模型，不仅在每个样本中产生约 5 次循环，图直径更大，而且展现出约 6 倍的显著小世界特征。随着任务难度和模型容量提升，这些结构优势更加凸显：14B 规模模型的循环检测率达到峰值，32B 规模模型的探索直径最大，并与模型准确率呈正相关。此外，针对更优数据集进行的有监督微调也能系统性地扩展推理图直径并提升性能，为数据集设计提供了有效指导。本文工作在理论与实践层面均为推理模型的可解释性与性能提升提供了新视角。

关键词：推理图（reasoning graph），循环结构（cyclicity），图直径（diameter），小世界指数（small-world index），有监督微调（supervised fine-tuning）

彭晨丨作者

赵思怡丨审校

论文题目：Topology of Reasoning: Understanding Large Reasoning Models through Reasoning Graph Properties

论文链接：https://arxiv.org/abs/2506.05744

发表时间：2025年6月10日

近年来，以 OpenAI‑o1、Gemini、Claude、Grok 及 DeepSeek‑R1 为代表的大规模推理模型，通过延长“思考”过程而在编程、数学、科学问题上取得突破性进展。然而，尽管蒸馏（distillation）和有监督微调等技术使更小模型也能模仿高级推理能力，其内部具体机制却始终不明。为深入剖析模型的推理行为，本文引入了“推理图”的概念：将模型在每一步推理时的隐藏态聚类为节点，再根据推理步骤的先后关系构建有向图，以此直观呈现模型在思考空间中的漫游和重访情况。

推理图的构建方法

推理图的构建分两步进行：首先，对每个推理步骤对应的 Transformer 隐藏层输出进行均值池化（mean pooling），然后借助 K-means 聚类将所有步骤映射到预设的簇中心，每个中心即为一节点。其次，按照模型生成的中间答题步骤顺序，将相邻两步对应的节点以有向边相连，得到完整的推理图。这个方法既可根据不同层深截取隐藏态，也能适配多种数学任务，充分捕捉模型推理路径的拓扑结构。

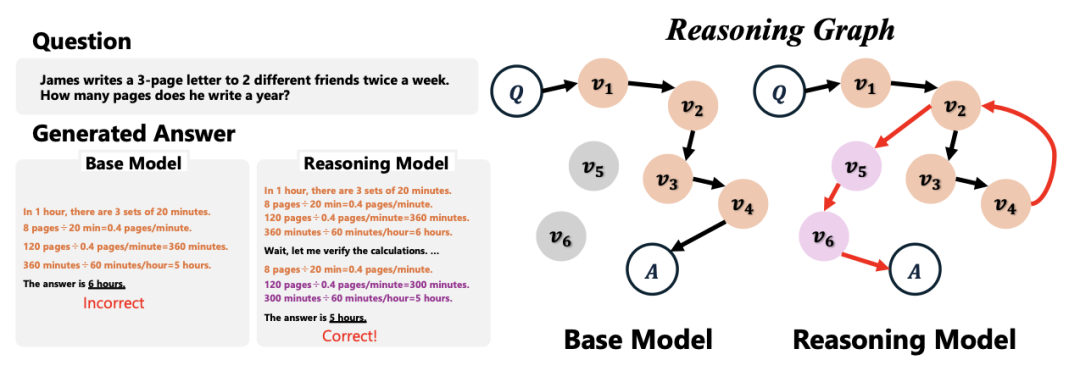
图 1. 推理图的概念，比较基本模型和大型推理模型。节点表示简单的计算状态（例如，左图所示的计算步骤），其中通向最终答案的路径构成推理图。我们分析了推理图的图论性质，包括循环结构、直径和小世界特征。研究这些结构上的区别使我们能够更好地理解最近在具有挑战性的数学任务中的表现改进。

研究使用了基础模型（Qwen2.5‑32B）与蒸馏模型（DeepSeek‑R1‑Distill‑Qwen‑32B）进行实验，对比它们在 GSM8K 上的 t-SNE 可视化，可以清晰地观察到后者推理图中频繁出现闭环（cycle）——模型会多次重访相同节点。进一步量化表明，蒸馏模型在所有测试样本中平均产生约五次循环，且循环检测率（cycle detection ratio）会随着任务难度从 GSM8K 到 MATH500 再到 AIME 2024 逐步上升，揭示出循环结构是模型反复检验和修正思路的重要表现。

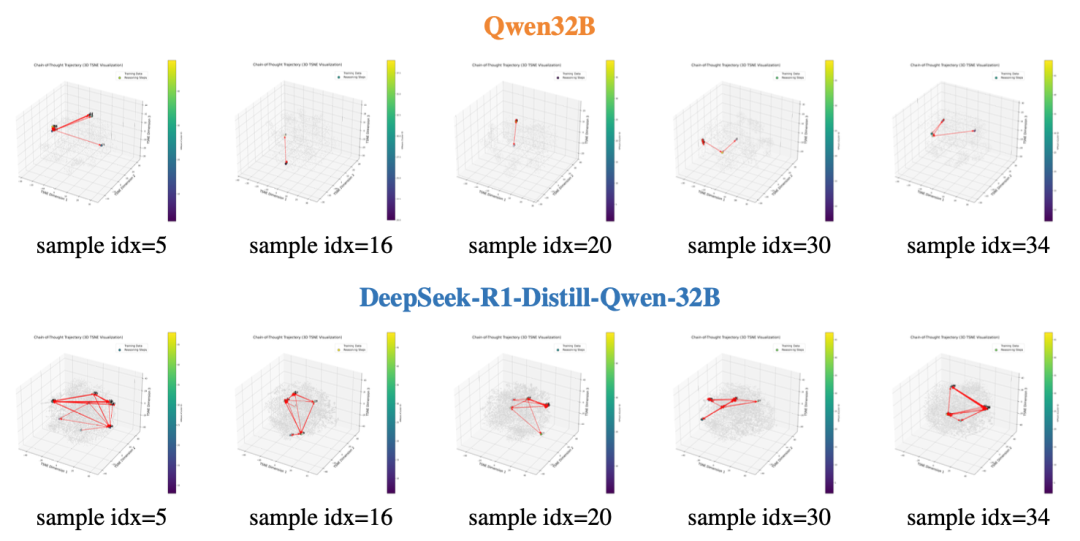
图 2. 基于t-SNE嵌入的GSM8K数据集推理图可视化。上图为基础模型（Qwen2.5-32B）的图，下图为大型推理模型（DeepSeek-R1-Distill-Qwen-32B）的图。与基本模型相比，推理模型在质量上的探索范围更广，其推理图中的循环明显更多。

推理图直径与小世界结构

图直径（diameter）定义为图中任意两节点最短路径长度的最大值，代表模型在推理时探索的最远状态距离。实验结果显示，蒸馏模型推理图的直径显著大于基础模型，且随着隐藏层深度增加而持续增长，表明更深层的特征有助于模型遍历更广泛的推理空间，从而支持更复杂的数学推理策略。

小世界指数（small-world index）刻画了图的局部聚集性与全局连通性之间的平衡。经对无向化后的小世界指数分析，蒸馏模型的推理图在保持高聚集系数的同时，仍具备较短的平均路径长度，使得模型不仅能在局部快速恢复思路，也能通过少量跳转快速抵达全局关键信息。这一结构特征从网络科学角度解释了推理模型为何能兼顾连贯性与效率。

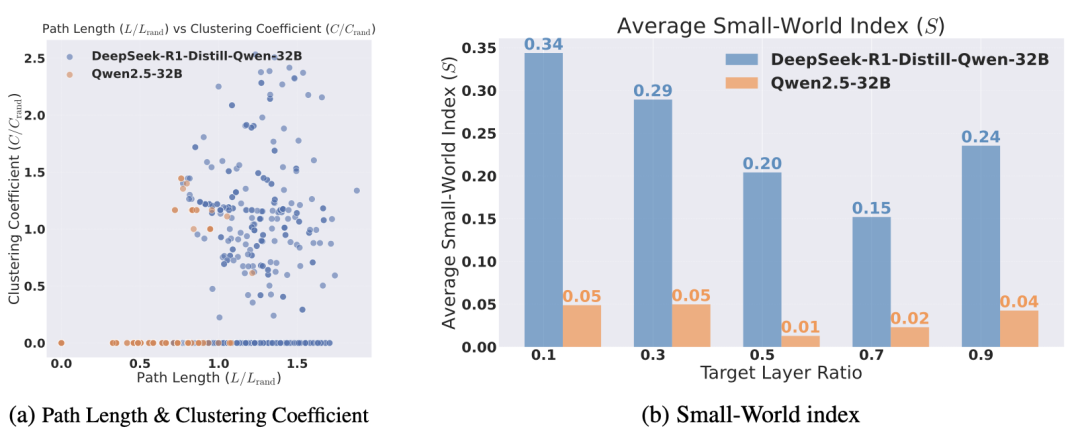
图 3. 大型推理模型（DeepSeek-R1-Distill-Qwen-32B）和基础模型（Qwen2.5-32B）的平均路径长度和聚类系数分布。推理模型具有较大的聚类系数和较长的路径长度，表明推理节点聚类密集但分离广泛。（b）由聚类系数计算的小世界指数与平均路径长度的比较。在所有层中，与基本模型相比，推理模型始终表现出更高的小世界特征。

模型规模对推理拓扑的影响

由 1.5B、7B、14B 到 32B 多个规模模型的对比揭示，循环检测率随规模增长而上升，在 14B 时达到峰值，但 32B 模型因出现少量语言混杂（language mixing）循环略有下降；循环计数和图直径则随规模持续提升，并与模型在 AIME 2024 上的准确率高度相关。这表明，更大模型容量不仅能够增加模型修正思路的机会，还能拓展推理路径的广度，进而提升综合表现。

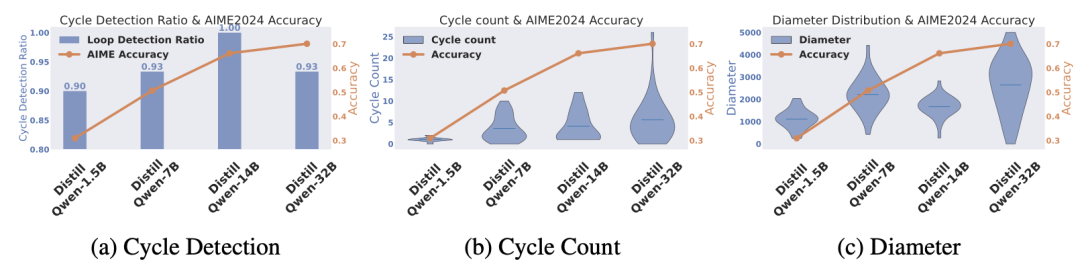
图 4.（a）不同模型尺寸下循环检测率与AIME 2024准确率的关系。循环检测率一般随着模型大小的增加而增加，达到14B，达到100%的循环检测率。然而，准确率最高的32B模型与14B模型相比，循环检测率略低。（b）不同型号的循环次数与准确率之间的关系。较大的型号显示出增加的循环计数，32B模型达到最高的准确率，显示出最多的循环次数。（c）不同模型尺寸下推理图直径与准确率的关系。32B模型，实现最高的准确率，也显示最大的图形直径。

结论与展望

本文通过推进“推理图”的概念，将复杂的隐藏态序列转化为可视化的网络拓扑，并从循环结构、图直径与小世界指数三方面揭示了大规模推理模型的内部机理。研究不仅为“顿悟时刻”（aha moment）和过度/欠缺思考（overthinking/underthinking）等现象提供了新的解释，也为构建更有效的微调数据集指明了可量化的设计指标。未来，我们期待将推理图方法扩展到更多场景，融合动态自适应聚类与因果分析，为可解释 AI 与模型改进开辟新路径。

大模型可解释性读书会

集智俱乐部联合上海交通大学副教授张拳石、阿里云大模型可解释性团队负责人沈旭、彩云科技首席科学家肖达、北京师范大学硕士生杨明哲和浙江大学博士生姚云志共同发起「大模型可解释性」读书会。本读书会旨在突破大模型“黑箱”困境，尝试从以下四个视角梳理大语言模型可解释性的科学方法论：

自下而上：Transformer circuit 为什么有效？

自上而下：神经网络的精细决策逻辑和性能根因是否可以被严谨、清晰地解释清楚？

复杂科学：渗流相变、涌现、自组织等复杂科学理论如何理解大模型的推理与学习能力？

系统工程：如何拥抱不确定性，在具体的业界实践中创造价值？

五位发起人老师会带领大家研读领域前沿论文，现诚邀对此话题感兴趣的朋友，一起共创、共建、共享「大模型可解释性」主题社区，通过互相的交流与碰撞，促进我们更深入的理解以上问题。无论您是致力于突破AI可解释性理论瓶颈的研究者，探索复杂系统与智能本质的交叉学科探索者，还是追求模型安全可信的工程实践者，诚邀您共同参与这场揭开大模型“黑箱”的思想盛宴。

读书会已于2025年6月19日启动，每周四晚19:30-21:30，预计持续分享8-10周左右。

详情请见：破解AI黑箱的四重视角：大模型可解释性读书会启动

6. 高考分数只是张入场券，你的科研冒险在这里启航！

7. 系统科学前沿十讲：理解自然、生命与社会的复杂性