Published on August 7, 2025 3:01 AM GMT
Project done as the capstone for ARENA 5.0. Write-up by Lucy Wingard, project team was Lucy Wingard, Gareth Tan, and Lily Li. Special thanks to David Quarel for help working through our various bugs.
See code here: https://github.com/garetht/absolute_zero_reproduction
What is Absolute Zero?
Absolute Zero [1]is a recently developed RLVR (reinforcement learning with verifiable rewards) technique to achieve SOTA math and coding performance using self-play and zero data.
Why is this important?
Generating high-quality data is expensive, often relying on human validation - particularly with the shift to reasoning models that require long and correct reasoning traces for each question. Producing datasets of the necessary quality and scale to train better reasoning models might soon become unsustainable. Additionally, relying on human-curated data might constrain a model’s ability to eventually exceed human-intelligence levels on particular tasks.
The Absolute Zero Reasoner (AZR) paradigm removes the need for external data by having the model simultaneously learn to create learnable tasks and solve them effectively.
How does Absolute Zero work?
Let’s start with a simplified overview of standard RL. Skip this section if you are already familiar with how RL works.
Standard RLVR
In traditional RLVR environments a policy (aka a base LLM, or SFT’d LLM) is in an environment with a particular state, s0, and chooses an action a, that changes the environment to be in a new state, s1. This action a and new state s1 are given to a reward model (in a verifiable reward setting, this reward model can validate the state s1 against a ground truth, for example, determining whether the proposed answer to a math equation is valid). The reward model generates a reward, and then this reward is used to update the policy (either encouraging or discouraging the behavior that led to the current state).
AZR
In AZR, the policy both proposes and solves problems. The policy gets rewarded based on how “learnable” the problem it proposed was, and whether it was able to solve the problem.
The magic of AZR comes from decomposing each problem into 3 separate subproblems (or tasks): induction, abduction, and deduction. The policy must propose and solve a problem for each task type. These proposed problems and solutions are then added to a dataset from which the model can learn. This slide from our capstone presentation illustrates the concept nicely:

In the above diagram, the text bubbles represent what the policy creates when it is proposing. After validating that these proposed problems have the correct format, they are added to the dataset. Next, the policy is given problems sampled from the dataset to solve. These solutions are verified, and a joint reward is calculated based on whether the policy correctly solved the problem, and whether the problems proposed were learnable.
This diagram from the paper shows the general flow of this process:
Through this process, the policy builds up its own dataset to sample from. By starting with a single seed problem, this process is able to train SOTA math and coding models.
Replication process

We worked as a team of 3 with the goal to replicate this paper in ~5 days[2]. The paper reported training Qwen-2.5-7B on 4 A800s for ~60 hours. In an effort to make this process faster we opted for 2 big changes[3]:
1. Using a 3B model, and
2. Constraining the problem type: rather than considering the set of all possible verifiable python functions, we constrained our 'functions' to the set of prime inversion congruence relations.

We could control the difficulty of this task by constraining the max size of p, which allowed us to start training with problems that were well-suited to our model’s capabilities (i.e. the model could solve seed problems ~25% of the time).
A brief summary of what we wrote:
- Data storage and sampling infrastructureAdvantage, reward, and objective calculationsRollout phase (model acting as proposer and solver for each task type)Learning phase (calculating objective and doing gradient update)Eval functions (to validate model outputs and measure model accuracy at solving problems)
A non-exhaustive list of things that went wrong:
- Matching the pseudocode to the implementation on the authors’ github. We hoped that their implementation might be a source of truth for our reference, but their repo handles many cases/functionality not mentioned in the paper and is rather complicated. We mainly wrote directly from the pseudocode.Blowing up CUDA memory because we were storing tensors that had d_vocab as a dim unnecessarily.Blowing up CUDA memory because we didn’t have enough parallelization.Blowing up CUDA memory because we had too much parallelization.Not being able to backprop because we used initially model.generate() (which is wrapped in torch.no_grad) instead of model().Tensor shape mismatches.
For an in-depth look at our replication I recommend looking through our github repo.
Our results
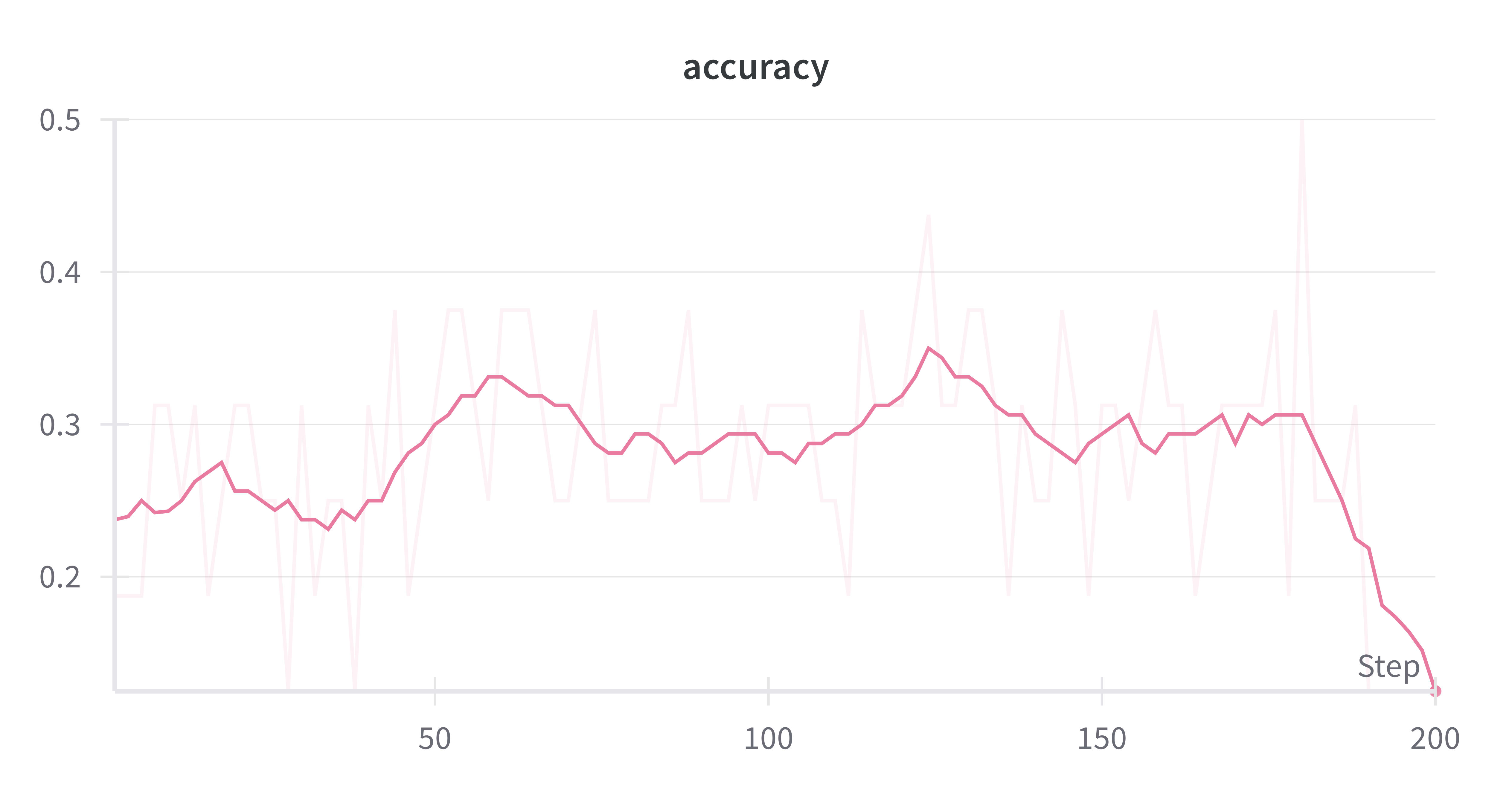
We evaluated the model's accuracy acting in the solver role on answering a held-out set of problems (which we referred to as the learning phase accuracy). We also tracked the rewards per role and task type throughout training to see if we could observe anything about when the model learned particular role/task behavior.
Over the course of 200 epochs, we observed the learning phase accuracy increase by ~10 percentage points. The reward across all task types for the proposer role remained quite low until step 180 - interestingly, there was a corresponding drop in learning phase accuracy. The solver accuracy was consistently low due to inability to correctly format responses. To better understand these results, let’s take a deeper look into the reward functions and training setup.
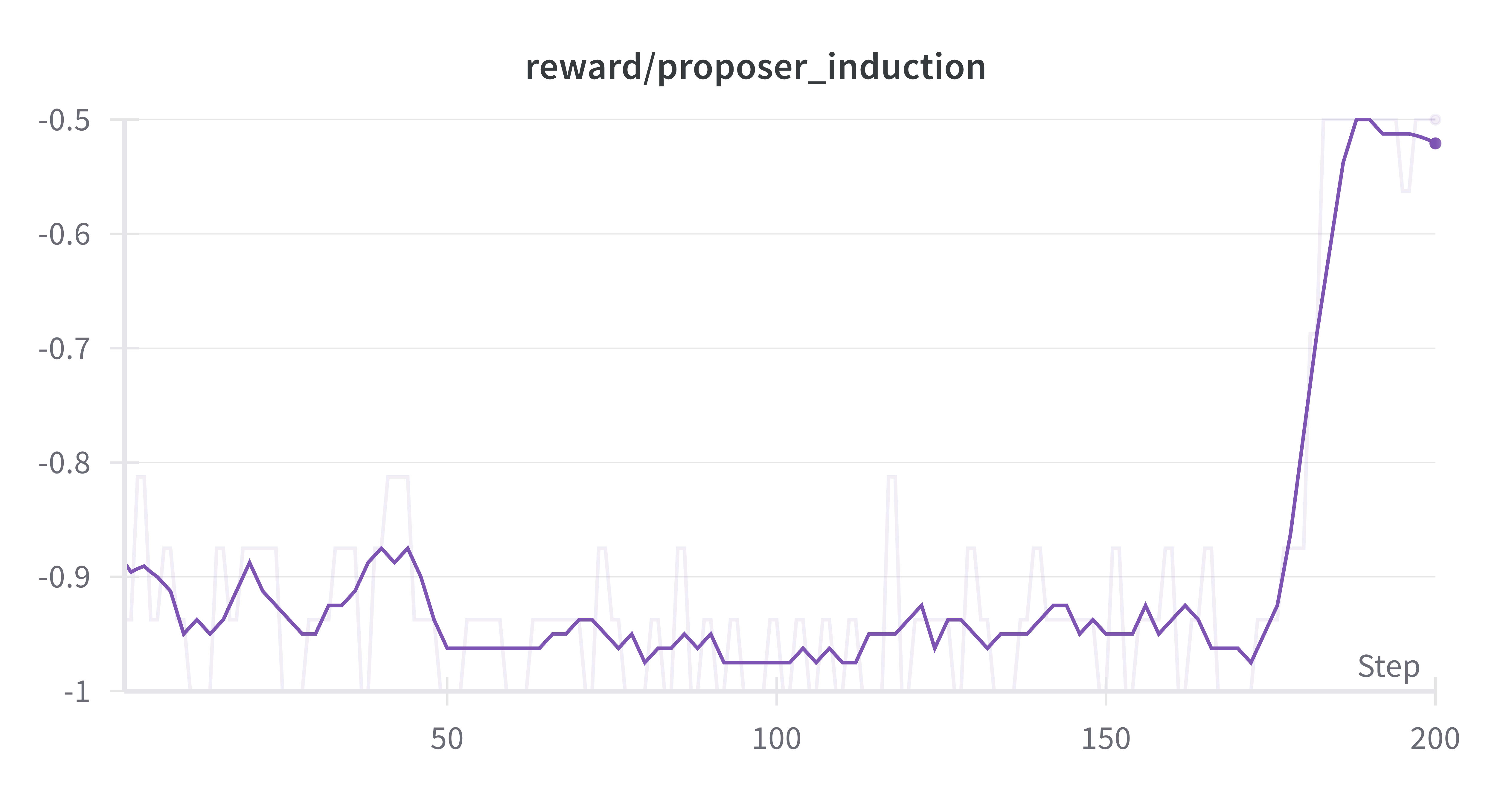
AZR uses 2 reward functions, one for each role (proposer and solver). In each function, if the model’s response was not formatted correctly, it received a negative reward. During the rollout phase, we first generate model responses under the proposal role. We then calculate a partial reward for these responses - if the response has correct formatting, we then use it as the prompt during the solver phase. However, if the response had incorrect formatting, we rely on pre-generated prompts during the solver phase.
The final proposer reward is based on how “learnable” the problem it generated was - if the model can solve it 100% of the time the problem is considered too easy and the r_proposer is 0; if the model can solve it 0% of the time the problem is considered too hard and r_proposer is 0.
The spike in proposer reward represents the point where the model finally learned to correctly format its responses - we can see that the reward moves from negative to 0. At the same time we see a drop in the corresponding learning phase accuracy - my assumption here is that learning to correctly format proposed questions somehow caused a regression in ability to correctly format or solve the held-out questions. I think it's possible that this represents a local dip in the training and that a longer training run would have given the model a chance to learn formatting and correctness across both proposing and solving problems.
Next steps
Immediate next steps for this project would be to try running our code for more epochs (to validate the theory that learning phase accuracy would continue improving after using model-generated problems), and on a bigger model. I'd also like to adapt our code to work with generic Python functions (like the original paper) and see if the results still hold, as well as training on a non-Qwen model to see how this paradigm generalizes.
- ^
- ^
At the time of our replication new results were released showing Qwen models can be trained with spurious rewards and still learn https://rethink-rlvr.notion.site/Spurious-Rewards-Rethinking-Training-Signals-in-RLVR-1f4df34dac1880948858f95aeb88872f . We did not have time to test the AZR setup on a non-Qwen model but look forward to exploring that in future work.
- ^
Also, several smaller changes such as reducing generation length and number of rollouts
Discuss



