Published on August 1, 2025 6:37 PM GMT

Drawing inspiration from the ‘brain in a vat’ thought experiment, this blogpost investigates methods to simplify world models that remain agnostic to the agent under evaluation. This work was done together with Alec Boyd and Manuel Baltieri, with support from the UK ARIA Safeguarded AI programme and the PIBBSS Affiliateship programme. The post presents general ideas avoiding technicalities as much as possible, please refer to the preprint for formal details. Thanks to @Alexander Gietelink Oldenziel and @Lucas Teixeira for suggestions on this writeup.

Introduction

World models are typically conceived as tools for model-based reinforcement learning agents to improve their task performance. Interestingly, recent works are proposing a new perspective: world models can also be used as virtual environments where AI agents can be tested without real-world consequences. These simulated environments are ideal for evaluating how AI agents handle edge cases and respond to novel situations, potentially revealing safety issues. Furthermore, world models are also promising for building formal certificates of safety.

The efficacy of these approaches critically rely on the world model adequately representing real environments. To ensure that assessments of AI agent behaviour may transfer from simulations to a real-world setting, world models must faithfully reflect the real world’s structure and dynamics. Thus, a key challenge lies in dealing with the computational demands of high-fidelity simulations.

A crucial insight is that world models only need to incorporate the variables that make a difference for the agent. Building on this idea, we introduced a framework to investigate world modelling from the perspective of an external entity in charge of sandboxing an agent. The proposed framework does not require knowledge of the agent’s policy, and make no assumptions about the agent’s architecture and capabilities — being applicable to systems irrespective of how they were designed or trained.

The main take-home messages of this blogpost will be:

efficiency-vs-interpretability

^[1]

trade-off

These conclusions lead to a number of practical recommendations to guide designers when constructing world models, which we will also discuss.

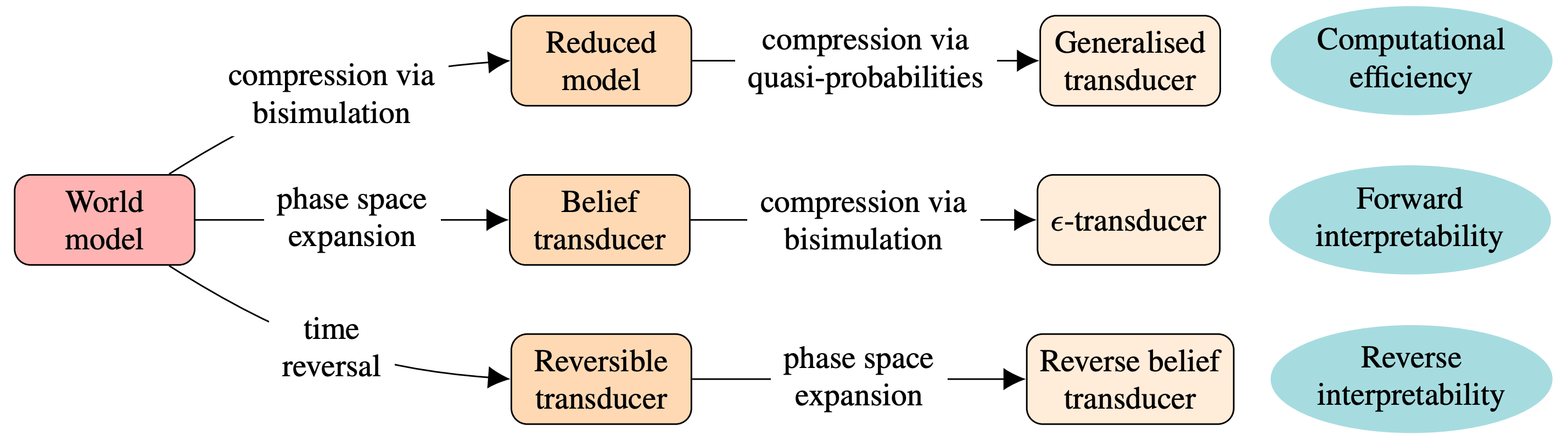
Foundational ideas

"Representation and what is represented belong to two completely different worlds" — Henrich von Helmholtz (Handbuch der physiologischen Optik, 1867)

Let’s consider how one could construct a world model to sandbox a simple a vacuum cleaner robot. While one could in principle run a simulation that includes the quantum dynamics of the whole planet, such simulation would be not only computationally unfeasible but also unnecessarily complex to address most practical questions related to the robot. Such a world model would be too spatially extended (including regions of the planet that are inaccessible to the robot) and would include too many details (including quantum effects for a fundamentally classical system). A smart designer could instead choose to build a more efficient world model that factors out properties that make no difference for the robot.

Related questions have been extensively investigated by philosophers and cognitive scientists for decades^[2] (or centuries!). These investigations highlight the fact that, while an agent’s actions turn into outcomes due to the mediation of the external world, the agent has no direct access to the world and only interacts with it via its actions and outputs.

These ideas can be traced all the way back to Immanuel Kant, who proposed that to understand how ‘knowledge’ works one should switch the attention from the properties of external world to the characteristics of the observer — i.e. from the known to the knower. Kant’s ideas were tremendously influential, leading to a new wave of aesthetics where subjectivity takes a central stage, and also to a new generation of scientists investigating the workings of the human mind from the inside-out. Particularly important in this regard was the work of Henrich von Helmholtz, who is well-known today not only for his contributions to thermodynamics but also for his work on the nature of sight. Inspired by Kant, Helmholtz came with the idea that what we experience through vision may be radically different from how things actually are.

This whole set of ideas is colourfully encapsulated by the classic ‘brain in a vat’ thought experiment. This thought experiment suggests that if organism’s brain were to be placed inside a vat, and a computer is used to read the brain’s output signals (e.g. motor commands) and generate plausible input signals (e.g. sensory information), then the brain may not be able to tell that it is inside a vat. This thought experiment is an useful intuition pump for thinking about the nature of the mind, having roots in Descartes’ evil demon and Plato’s cave allegory, and inspiring tons of academic discussions and popular media such as The Matrix movies.

The 'AI in a vat' perspective

The previous ideas suggests that a world model can be reduced by focusing on the agent’s perspective — i.e., what affects it, and what it is affected by it. Concretely, a minimal world model for sandboxing an AI agent should ideally depend only on three key elements:

^[3]

Using just those ingredients, it should be possible — at least in principle — to build a compressed representation that encapsulates the effective world of an AI agent, such that it cannot be distinguished from a full simulation, irrespective of how smart or powerful the agent may be.^[4]

Following this ‘AI in a vat’ perspective, the proposed approach is not to restrict ourselves with a particular world model, but instead to follow a three-step strategy:

Delineate the class of world models that are indistinguishable from the AI agent’s perspective.Characterise their relative strengths and weaknesses.Identify principles for choosing specific models depending on distinct priorities.

Following these ideas, let's now formalise the ideas of interface, world model, and transducer.

Interfaces

An interface characterises the 'viewpoint' of an agent by establishing how it interacts with its environment (see Definition 1 in the preprint). Concretely, an interface is a collection of probabilities for sequences of outcomes ( $Y_{0}, Y_{1}, Y_{2}, \dots$ ) conditioned on sequences of actions ( $A_{0}, A_{1}, A_{2}, \dots$ ). This can be thought of as a discrete-time stochastic process (i.e. a time-series) conditioned in another.

The interfaces captures the perception-action loop that links the agent with its environment, being independent of the agent's policy (as actions only condition the process). Although they may presuppose some 'external world' transforming actions into outcomes, they don't exhibit this world explicitly. As such, they describe 'the experience of the world' as seen from within the agent.

Unfortunately, interfaces on their own can be extremely inefficient to sample — and hence for running simulations.^[5] Making them easier to run is what world models do.

World models

We define world models as auxiliary variables that make the calculation of interfaces feasible (see Definition 2 in the preprint). We request of world models to satisfy one key property:

contain all the relevant information

World models yield an elegant factorisation of the joint probability of outcomes given actions. This factorisation provides an efficient method to sample trajectories of outcomes given trajectories of actions and world states in a very simple way^[6].

Transducers

Transducers are models of stochastic machines that receives inputs and generates an output while updating its internal state (see Definition 3 in the preprint and also here). The core of an automata is a stochastic kernel $κ (y_{t}, s_{t + 1} | a_{t}, s_{t})$ , which determines the probability of generating a given output $y_{t}$ and next internal state $s_{t + 1}$ given a previous state $s_{t}$ and action $a_{t}$ . The name 'transducer' comes from the idea that they transduce inputs into outputs, while keeping an internal state that serves as memory.^[7]

Transducers give a natural way to factorise interfaces and compute them sequentially according to the following graphical model (see Lemma 2 in the preprint):

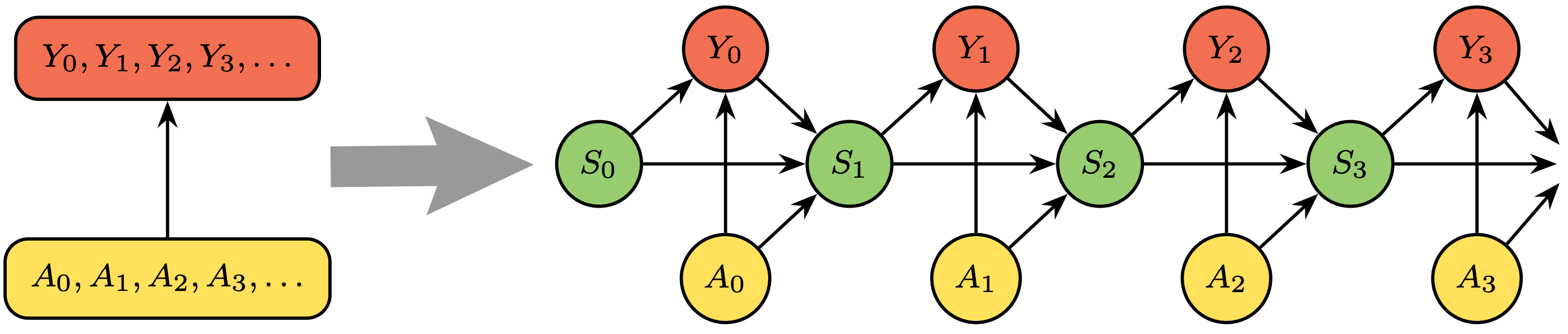
Transducers generalise partially observed Markov decision processes (POMDP), whose kernels obey specific independency properties that make the next world state independent of the outcome — which comes handy when modelling 'objective' physical processes that are not affected by the observer. Interestingly, transducers also account for world models that reflect epistemic processes, as we discuss below.^[8]

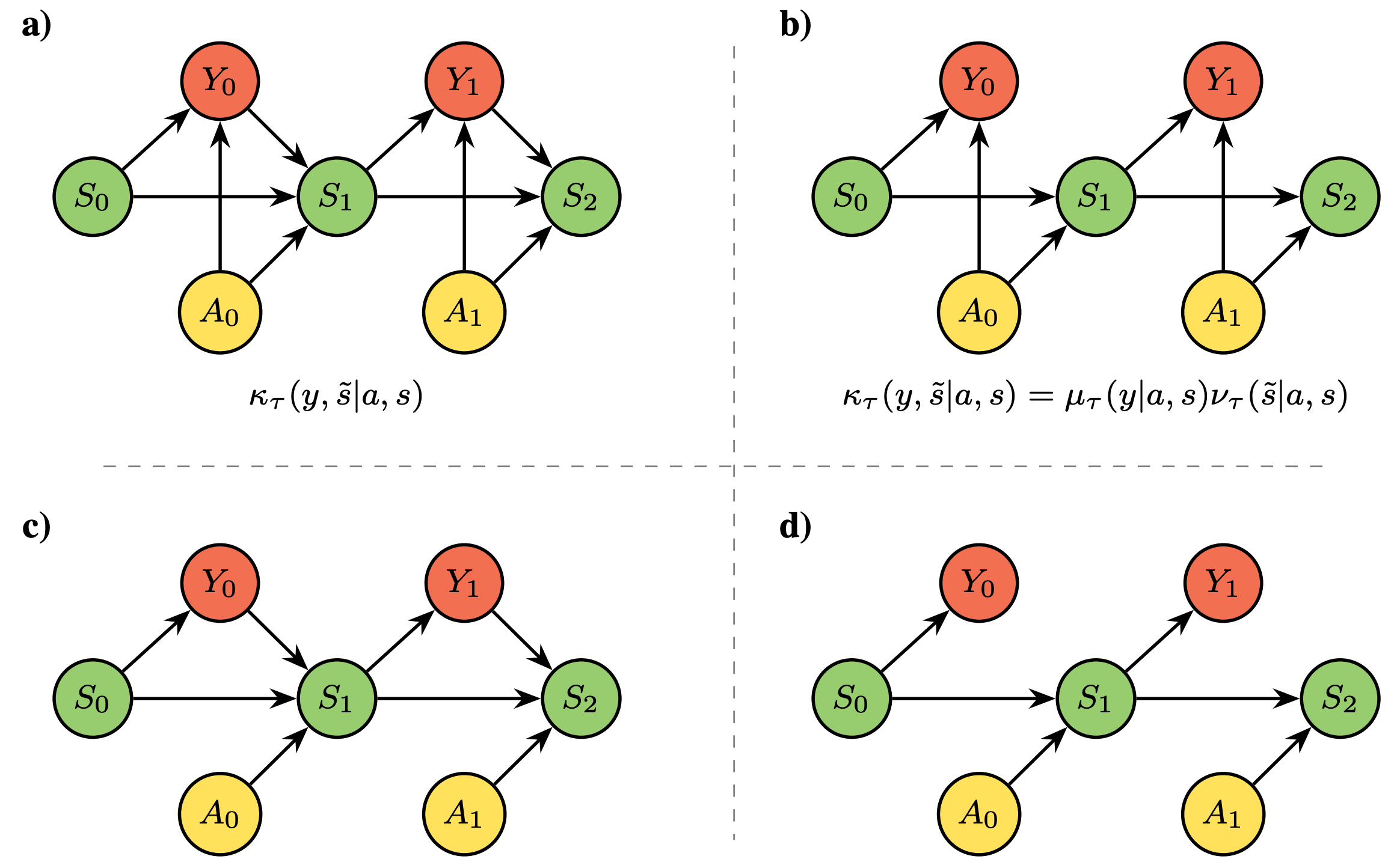
Different types of transducers: most general form (a), POMDP with action first (b) or outcome first (d), and belief transducers that reflect epistemic states (c).

Before concluding this section, let me present an example that illustrates how a given interface can be generated by various world models with different properties.

Example of interface and world models

Consider a robot that is manipulating a deck of cards. This can be described with a world model with $13! \approx 6 \times 10^{10}$ possible states, corresponding to the possible arrangements of the deck. Let's say that the robot can take two possible actions: either it puts the front card in the back ( $α_{1}$ ) or it shuffles the deck ( $α_{2}$ ), so that $A_{t} \in {α_{1}, α_{2}}$ . Additionally, the robot observes the card that is on top of the deck. However, let's assume that the sensory apparatus of the robot is not capable of reading the number or the suit of the card, but only its colour. Hence, the possible outcomes for the robot satisfy $Y_{t} \in {black, red}$ .

In this scenario, the interface of the robot is the collection of probability distributions of the form $p (y_{0 : t} | a_{0 : t})$ relating sequences of actions with sequences of outcomes. This interface can be implemented via a transducer with internal state $S_{t}$ tracking the state of the deck. Note that implementing the kernel of this transducer on a computer would require a substantial amount of memory due to the large number of possible world states.

Alternatively, one could forget about the fact that there is an underlying deck of cards and focus on the sequences of colours that the agent records. By doing this, one may notice that, given a sequence of actions and outcomes $(a_{0 : t}, y_{0 : t})$ , the only information that is relevant to predict the next outcome $y_{t + 1}$ is the number of red and black cards observed since the last time the agent took action $α_{2}$ (shuffling the deck). Hence, one could build a simpler transducer whose memory tracks only this information in the form of an internal state $M_{t}$ . This would be an ‘epistemic’ world model that reflects the agent’s state of knowledge, contrasting on the previous one that reflects an objective physical process taking place ‘out there’.

Note that $M_{t}$ can take only roughly ~ $10^{2}$ states instead of ~ $10^{9}$ , requiring substantially fewer memory resources. Furthermore, $M_{t}$ reflects all the relevant information that an agent with this particular interface (i.e. limited to recognising colours) could ever want to take into account in order to make informed actions in this scenario. Therefore, this new world model is not only more memory efficient, but also reveals what information an agent of this kind could have incentives to learn.

Minimal world models

Above we saw that the complexity of a world models depends on how complicated is the memory structure of the interface that it is factorising. This can make one wonder: is it possible to find a minimal world model that can give rise to a given interface? The notion of minimality can be instantiated in different ways — to keep things simple, let’s focus on minimising the number of world states (which is related to the memory cost of encoding such a world model into an actual computer).

At this point, one may wonder what happens if a given interface cannot be generated by any transducer. Luckily, there always exists at least one transducer that generate any interface (they are usually many more than one!). For example, a world model that keeps recordings of everything that have happened (in terms of actions and outcomes) always gives a valid transducer. Admittedly, such model is not very memory-efficient — just as Borges’ character Funes the memorious, this world model does not forget anything, and hence its implementation would require an unbounded amount of memory. Thus, we can now focus on the following question: how can one reduce/simplify a given transducer?

Bisimulation

The standard way to reduce world models in the RL literature is via bisimulations. Put simply, bisimulation is to collapse world states that are functionally equivalent.^[9]

Perhaps surprising, it can be shown that direct bisimulation of a given world model may not attain maximal efficiency. This means that the minimal bisimulation of two world models of the same interface may not be isomorphic!

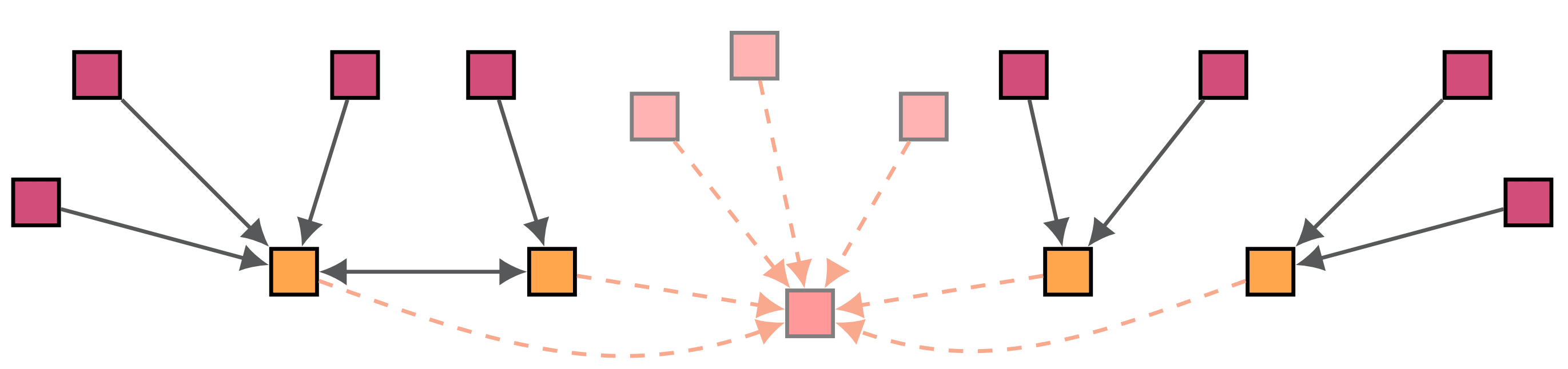
Illustration of the minimisation of world models. Purple boxes represent reducible models and
orange boxes represent minimal ones, and arrows correspond to reductions. Red boxes are generalised models following quasi-probabilities, which (if allowed) establish global minima.

This implies that to reduce all redundancies and obtain a unique minimal world model, we need a reduction process that goes beyond coarse-grainings — which we explain next.

Bonus: why bisimulation may not be enough

To understand the limits of bisimulation, one can analyse the probabilities of generating different sequences of outcomes given actions by initialising the transducers at different states (conditioned on corresponding sequences of actions). This gives, for every world state, a vector of probabilities per possible sequence. The idea is consider increasingly long such sequences, and see if the vectors corresponding to different world states span all the dimensions available for them. If they don’t, no matter how long the considered outcome sequences, that means that there is some redundancy in the world states.

The limitations of bisimulation can be seen by considering the matrix of such vectors.^[10] Bisimulation can only merge states, which is equivalent to check the rows of that matrix and reduce them if they are equal. However, it could be than three or more states have all different rows, but nonetheless are linearly dependent (interestingly, this can only happen between three or more vectors!). And the problem is that coarse-grainings are not powerful enough to reduce such dependencies.

Quasi-probabilities and generalised transducers

Remember how, in calculus, the theory of power series is tremendously cumbersome in the reals to become elegant and simple in the complex domain? A similar move — achieving a simpler theory by switching to a more abstract space — happens for transducers, and the key relies in quasi-probabilities.^[11]

When their memory can only take a finite number of states, transducers can be conceived as collection of substochastic matrices (with non-negative numbers whose row sums are less or equal than one) such that, when multiplied together, they give the right probabilities for the outcomes.^[12] Hence, the problem of finding a minimal transducer can be reframed as finding substochastic matrices that make the numbers work. And stands to reason that, if such optimisation problem is faced with less restrictions (e.g. the coefficients can be negative), then the optimal solution will be better.

Example of quasi-probabilities

Imagine flipping a funny coin with three sides ${a, b, c}$ , where each side has an associated quasi-probability given by $(q_{a}, q_{b}, q_{c}) = (0.5, - 0.1, 0.6)$ . Because of the negative term, we cannot simply sample events following such frequencies. However, if we suddenly become unable to differentiate between events $b$ and $c$ , this would result on our funny coin turning into a standard fair coin. Similarly, if we stop differentiating events $a$ and $b$ , then the funny coin would turn into an unfair coin. Because of this, one can think of quasi-probabilities as unobservable 'sources' that can give rise to multiple somehow interrelated probabilistic scenarios — depending of how coarse-grainings are implemented. As such, it is not surprising that quasi-probabilities arise naturally in quantum mechanics.

Unfortunately, generalised transducers achieve a minimal computational complexity at the cost of introducing an opaque, unobservable world model. Indeed, the world models of generalised transducers follow transitions with quasi-probabilities, which means that their states cannot be properly observed — as quasi random variables cannot be sampled in a meaningful way. This result on a substantial lack of interpretability, as this world cannot be describe as evolving between states in a probabilistic setting.^[13]

Epistemic world models

Let’s stop to do a brief recap. We started by looking for the most computationally efficient world models, but we found that they are generally highly uninterpretable. So, let’s now look for models that may not be the most efficient ones but have interpretable features — in the sense that they help us to assess and understand the capabilities of the corresponding agent.

To start, let’s consider some properties that may be desirable from a world model:

observable

unifilar

Hence, observable models are useful for interpretability as they correspond to models that an agent could estimate online while doing things, and unifilar models are the ones that can be efficiently updated.

World models of beliefs

One way to build observable models is to do Bayesian inference over the hidden states of a given world model. ^[14] Beliefs are probability distributions over those states, and assuming that the agent learns from observations in an optimal manner, we can assume that those beliefs evolve following Bayes' rule.^[15] Interestingly, Bayes rule induces specific dynamics between those beliefs that let the agent to update beliefs without the need to recalculate all every time from scratch. This leads to a unifilar transducer that encodes the belief updating processes, which we call belief transducer.

Belief transducers are alternative world models for the same interface (see Proposition 2 in the preprint). This idea is known in RL as belief MDP: for a given partially observed scenario, one can always build an equivalent fully observed scenario of beliefs that is essentially equivalent to the original one — in the sense that an optimal policy to the later directly translates into an optimal policy to the former.

In summary, this process of 'belification' extends the world's phase space (from states to distributions between those states) to make it observable.

Minimal belief models

Belief models are usually not efficient. These models usually include different beliefs (i.e. probability distributions) that are nonetheless functionally equivalent to the agent, in the sense that they lead to the same downstream predictions. This makes one wonder: what would it happen if one bisimulates beliefs? This would make sense, as by expanding the phase space of the world, it is very likely that many different belief states are statistically equivalent to each other.

How far the bisimulation of beliefs can go? The answer is: surprisingly far.

Do you remember the finding that bisimulation is in general less efficient than going wild with negative probabilities? Well, the good news is that the situation is different for observable models: a canonical minimal belief model, known as ‘ε-transducer’, is found by bisimulating any predictive model (see Theorem 3 in the preprint). The uniqueness of the ε-transducer implies that the refinement of the beliefs of any optimal predictive agent must eventually reach this model, regardless of the world model the agent uses.^[16]

This is a remarkable result: say we have the agent above watching colours and imagining animals, and let’s say there is another agent having the same interface, but who is not imagining animals but galaxies of various shapes. These two world models are very different: they could substantially differ in size, and also in how their internal dynamics work. However, this result guarantees that, when simplified, the beliefs of those agents are perfectly equivalent! Thus, this guarantee that even if those agents are having quite a different “experience” (in the sense that they explain what they perceive in substantially different terms), they can always communicate to each other as they agree in what makes a difference. Another way to say this is that agents with same interface may have different metaphysics, but must agree on what is empirically verifiable. Perhaps this result is at the basis of the possibility of communication between agents...

In summary, while the compression of general world models is a pain — resulting in negative probabilities and all that jazz — the compression of observable models leads to a unified minimal model; the ε-transducer. Moreover, the above reasoning implies that the ε-transducer encapsulates all the predictive information that is available for agents to learn about their environments. In fact, the ε-transducer this is a direct generalisation of the geometric belief structure recently found in the residual stream of transformers.^[17] By studying the geometry of the ε-transducer one can identify what can be learned, and then evaluate to what degree a specific agent has access to these structures.

Retro-interpretability

It is natural to study the capabilities of agents in terms of their capabilities to predict future events and plan accordingly. A complementary perspective is to focus not on prediction but in retrodiction. For instance, one could identify undesirable outcomes, either in terms of world states that are unfavourable of sequences of actions or outcomes that are bad, and then ask which could have been the past event that made things to go that way.^[18]

Running worlds back in time would be indeed great, but is it possible? Is it possible to run a transducer backwards?^[19] If this is possible, one could take a future state and investigate what lead into it. Indeed, a retrodictive transducer could be employed in at least two manners:

For a given sequence of actions and world states, one can investigate which points of the trajectory were more important in determining a final outcome.One can do counterfactual analysis and see which are the precursors that can maximise or minimise the probability of reaching them.

Similar questions have been well investigated in theoretical physics, particularly thermodynamics and statistical mechanics, where irreversibility is closely related to the 'arrow of time'. These investigations have shown that Markov processes, and more generally hidden Markov processes, can always be ran back.

In this context, it is perhaps surprising to find that not all transducers can be run back. In order for a transducer to run back, it needs to satisfy specific conditions related to how state dynamics are affected by actions (see Theorem 4 in the preprint). Furthermore, we also present techniques to build retrodictive belief transducers even when the base transducer is not reversible (Section 6.2 in the preprint). I hope these first steps will foster new investigations exploring the potential of retro-interpretability for studying safety cases.

Conclusions

"Objects are not representations of things as they are in themselves, [...] but sensuous intuitions, that is, appearances, the possibility of which rests upon the relation of certain things unknown in themselves to something else." — Immanuel Kant (Prolegomena, 1783)

Overall, this work investigates the fundamental trade-offs in the design of world models for sandboxing and testing AI systems. The core principle is that there are many benefits to be gained if one instead focuses on the interface that characterises the viewpoint of the agent in consideration. Following this view, we were able to identify fundamental trade-offs inherent to world modelling.

The approach taken in this work complements the substantial body of work in RL that uses world models to boost the performance of agents, and work on representations from the point of view of the agent. Additionally, the ideas put forward here establish new bridges between related subjects in reinforcement learning and computational mechanics, and may serve as a rosetta stone for navigating across these literatures.

How practical can all this be?

Admittedly, the task of building a perfect synthetic environment for testing a super-intelligent system can seem daunting. However, given that large-scale foundation world model are starting to arise, the ideas and techniques elaborated in this work could be useful to reduce those synthetic environments, either to reduce the computational cost of agent evaluation or also to interpret the agent's capabilities.

However, an important limitation of this work is that it focuses on world modelling under the dictum of perfect reconstruction. This approach is useful for establishing general foundations, but will not take us far in practice. To make these ideas practically useful, we will need to investigate how to relax this constraint by aims to 'almost-perfect' reconstruction — where, of course, the key question is what 'almost' should mean. There are different alternatives, ranging from small average errors to min-max regret bounds. One exciting direction is to explore rate-distortion trade-offs in the construction of e-transducers, which could be combined with deep information bottlenecks.

Another promising direction to yield efficient modelling is to investigate how to exploit the compositional structure of the world (the fact that the world is not a undifferentiated 'blob', but it is made by pieces that interact in specific ways), perhaps utilising algebraic tools to analyse and factorise automata and the Krohn-Rhodes decomposition.

Final remarks

The new insights related to world models revealed in this work have implications not only for AI research, but also for cognitive and computational neuroscience, particularly pertaining the formal characterisation of the internal world (‘umwelt’) of an agent. These tools — together with the work being done by Simplex — are providing conceptual principles and computational tools to reverse-engineer the internal world model of agents from their interface, and could serve to differentiate what is grounded in the environment versus what is an 'hallucination'. These computational mechanics' based approaches are starting to provide tools to better understand why prediction alone can lead to the generation of internal world models. Combined with other recent work, all this may lead to updated accounts of some of the fascinating ideas from cybernetics, such as the internal model principle and the good regulator theorem — which may be critical for advancing our fundamental understanding of agents.

^{^}
Here I use the term 'interpretability' in a wide sense, referring to things that allow us to understand and interpret what AI systems can or cannot do. In fact, as explained below, the type of interpretability explored in this blog does not rely on analyses of internal states (like e.g. mechanistic interpretability does), but rather on using properties of the world model to infer the capabilities of agents.
^{^}
See for example the work from Andy Clark and Anil Seth, which develop the idea that our experience is not a passive apprehension of the world out there, but rather an active process involving our best predictions about it — a view known as predictive coding or the Bayesian brain.
^{^}
The outcome may be a combination of a quantity observable by the agent and a reward signal.
^{^}
This idea is well-known in physics, where effective theories capture how a given base theory looks like at specific spatiotemporal scales.
^{^}
Even considering an extremely simple robot with two possible actions and binary sensory inputs, a direct implementation of such a minimal interface could have an exponential number of degrees of freedom (one per each observation-action sequence, which in principle could be arbitrarily long).
^{^}
For a more technical explanation of the conditions that make a world model, see Definition 2 and Lemma 1 in the preprint. Note that general world models can be difficult to run, as their dynamics can be non-Markovian.
^{^}
Transducers are a perfect mix of classical automata (which transforms inputs to outputs while updating their state deterministically) and hidden Markov processes (which update stochastically but have no inputs).
^{^}
Note that some interfaces allow simpler world models than others. For example, a memory-less interface (where the action-outcome relationship is not affected by the history) can be generated by a trivial world model $S_{t} = 0$ . Also, the outcome itself can serve as a world model when the dependence on the history is Markovian — i.e. when all the relevant information for the future is contained in the last round (see Lemma 3 in the preprint). Fully observed Markov decision processes (MDPs) are examples of this.
^{^}
More technically, bisimulation is to identify world states that (i) emit outcomes with similar statistics and (ii) can be merged together without breaking the Markovian dynamics of the transducer (see Definitions 4 and 5 and Proposition 1 in the preprint).
^{^}
For a more technical discussion, see Section 4.2 in the preprint.
^{^}
Quasi-probabilities are numbers $q_{1}, q_{2}, \dots, q_{n}$ such that $\sum_{k} q_{k} = 1$ but some of them could be negative, hence relaxing one of the axioms of probability theory.
^{^}
See Equation (6) in the preprint.
^{^}
I like playing with the idea that perhaps all this story about quasi-probabilities provides a formal foundation to the Kantian notion of noumenon, which suggests that things-in-themselves are beyond our knowledge.
^{^}
For instance, imagine an agent with simple visual sensors that observe various sequences of colours. The agent could adopt a world model where the colours are caused by various animals that are walking in front of it, and by seeing specific sequences the agent can build beliefs of what is the animal out there. For instance, by seeing sequences of white and black the belief on a zebra is higher than a giraffe. In this setting, beliefs correspond to probability distributions over different animals.
^{^}
More specifically, beliefs evolve following equations given by Bayes filtering, which generalise Kalmann filtering to non-linear settings.
^{^}
A fun consequence of this is that the beliefs of the ε-transducer are isomorphic to the ε-transducer itself! For details about this, check Appendix O in the preprint.
^{^}
As a side-note for computational mechanics enthusiasts: although the update dynamics of the so-called mixed-state presentation (as shown e.g. in Equation 1 here) may look different to the standard update equation of belief states (as seen e.g. here), we found that these differences are consequences of time-indexing choices. Moreover, we found that POMDPs have two 'type' of beliefs — which we call predictive and postdictive), and their update rules are closely related to the predict-update process in Kalman and Bayesian filtering. For more details, please check Section 5.1 (particularly Proposition 3) in the preprint.
^{^}
Imagine there is one state of the world in which there are just too many paper clips: it would be useful for us to be able to run history backwards, and check which were the critical previous events that lead to that state of affairs.
^{^}
This question can be operationalised in the following way: we say a transducer with kernel $κ (y_{t}, s_{t + 1} | a_{t}, s_{t})$ is reversible if there exists another kernel $κ^{R} (y_{t}, s_{t} | a_{t}, s_{t + 1})$ such that the resulting input-output process is the same (see Definition 8 in the preprint).
^{^}
Transducers correspond to the world models (as defined above) that have Markovian dynamics .
^{^}
Note that these conditional probabilities should respect temporal precedence, so that future actions cannot affect the probabilities of past outcomes.
^{^}
We also ask them to respect temporal precedence, so their state is not affected by future actions.

Discuss