本文深入探讨了在多智能体强化学习（MARL）领域，智能体（Agent）如何学习相互理解和合作。文章首先介绍了智能体之间合作的经典难题，以及“对手塑造”（Opponent Shaping）这一理论框架。然而，早期主流的LOLA方法因计算成本高昂、数学复杂且难以直观理解而面临瓶颈。近期出现的“优势对齐”（Advantage Alignment）方法，成功地将对手塑造的核心思想提炼为一种简单、高效且计算成本低廉的机制，为AI-AI和AI-人类互动研究提供了新的思路和工具。文章详细阐述了这一演进过程，并分析了其在解决合作困境中的潜力和局限性。

### 传统AI智能体在合作中面临的挑战： 在经典的“迭代囚徒困境”（Iterated Prisoner's Dilemma）等合作博弈中，标准的、独立的强化学习智能体往往难以达成合作，通常会陷入相互“背叛”（Defect）的最差结果。这表明现有的强化学习算法在处理多智能体互动时的局限性，也引发了对未来AI系统在复杂社会性任务（如自动驾驶、金融交易）中能否有效合作的担忧。

### “对手塑造”理论的提出与LOLA方法的局限： “对手塑造”是一种通过模型化对手学习过程来影响其行为的强化学习理论。早期代表性方法LOLA（Learning with Opponent-Learning Awareness）试图通过计算高阶梯度（如交叉Hessian）来捕捉这种影响，从而使智能体能够预测并引导对手的学习。然而，LOLA在计算上极其昂贵，梯度估计方差大，且需要极高的透明度（了解对手的全部参数），这使得其在实际应用中难以落地。

### “优势对齐”（Advantage Alignment）的突破与优势： “优势对齐”（AA）方法是对LOLA的重大改进。它利用了强化学习中的“优势函数”（Advantage Function），将复杂的二阶梯度计算简化为一阶更新。AA通过将自身优势与对手的优势和共同历史相结合，形成一个“学习感知”的优势信号，从而在不增加计算负担且无需了解对手模型参数的情况下，实现与LOLA相似的对手塑造效果。这种方法不仅计算上更经济，而且在概念上也更清晰，使得智能体能更有效地学习合作策略，如“以牙还牙”（Tit-for-Tat）。

### AA方法对AI交互的意义与未来研究方向： 优势对齐的成功表明，通过精巧的算法设计，可以有效解决多智能体学习中的合作难题。它为AI-AI交互（如多机器人协同）和AI-人类交互（如AI辅助决策、AI治理）提供了新的分析工具和实践基础。尽管AA方法在某些假设下（如完全可观测环境、对手的价值函数可估计）表现最佳，但其研究也指向了未来需要解决的挑战，包括如何处理更不透明、能力差异更大的对手，以及如何扩展到大规模多智能体系统，以应对更广泛的实际应用场景。

Published on August 1, 2025 7:50 AM GMT

How do autonomous learning agents figure each other out? The question of how they learn to cooperate—or manipulate one another—is a classic problem at the intersection of game theory and AI. The concept of “opponent shaping”—where an agent models how its actions will influence an opponent’s learning—has always been a promising framework for this. For years, however, the main formalism, LOLA, felt powerful but inaccessible. Vanilla reinforcement learning is built around complicated nested expectations and inner and outer loops which layer upon one another in confusing ways. LOLA added high-order derivatives to the mix, making it computationally expensive, not-terribly plausible, and, frankly, hard to build a clean intuition around.

That changed recently. A new method called Advantage Alignment managed to capture the core insight of opponent shaping without the mathematical baggage. It distils the mechanism into a simple, first-order update that is both computationally cheap and analytically clearer. For me, this feels extremely helpful for reasoning about cooperation, and so I have spent some time unpacking it. I wanted a solid model of opponent shaping in my intellectual toolkit, and Advantage Alignment finally made it feel tractable.

This post lays out what I have learned from this setting. We start with the core puzzle of why standard learning agents fail to cooperate, trace the evolution of opponent shaping, and explore what this surprisingly simple mechanism implies for research directions in AI-AI and AI-human interaction.

Epistemic status

I’m an ML guy, but not an RL guy. This post is my attempt to educate myself. Expect errors. Find the errors. Tell me about them.

Setup

The Iterated Prisoner’s Dilemma (IPD) is a cornerstone method for modelling cooperation and conflict. You likely know the setup: two players repeatedly choose to either Cooperate (C) or Defect (D), with payoffs structured such that mutual cooperation is better than mutual defection, but the temptation to defect for a personal gain is always present.

Let’s lay out the payoff matrix to fix notation

	Alice: (C)	Alice: (D)
Dan: C	$(R,R)$	$(S,T)$
Dan: D	$(T,S)$	$(P,P)$

where captures the dilemma.^[1] The classic takeaway, famously demonstrated in Robert Axelrod’s tournaments, is that simple, reciprocal strategies like Tit-for-Tat can outcompete purely selfish ones, allowing cooperation to emerge robustly from a soup of competing algorithms.

For decades, the analysis of such games did not model the learning process in any modern sense.^[2] Agents would devise strategies by brute reasoning from a fully-specified game. Neither partial information about the game itself, nor computational tractability was a thing.

In the AI era, we care about the dynamics of learning — Can I build an agent that will learn such-and-such a strategy? What does my analysis of that learning algorithm tell me about feasible strategies and dynamics? The learning-oriented paradigm for game theory in intelligent, autonomous systems is multi-agent reinforcement learning (MARL). Instead of programming an agent with a fixed strategy, we design it to learn a strategy—a policy for choosing actions—by interacting with its environment and maximizing its cumulative reward through trial and error, i.e. reinforcement learning.

So, we ask ourselves, in these modern MARL systems what kind of behaviour can agents learn in the Prisoner’s Dilemma? These are not static, hand-coded bots; they are adaptive agents designed to be expert long-term planners. We might expect them to discover the sophisticated, cooperative equilibria that the folk theorem tells us exist.

Nope. When you place two standard, independent reinforcement learning agents in the IPD, they almost invariably fail to cooperate. They learn to Defect-Defect, locking themselves into the worst possible non-sucker outcome.

This failure is the central puzzle of this post. MARL is our primary model for how autonomous AI will interact. If our best learning algorithms can’t solve the “hello, world!” of cooperation, what hope do we have for them navigating the vastly more complex social dilemmas of automated trading, traffic routing, or resource management?

Opponent shaping ^[3] is a reinforcement learning-meets-iterated game theory formalism for multi-agent systems where agents influence each other using a “theory of mind” model of the other agents (or at least a “theory of learning about others”). I’m interested in this concept as a three-way bridge between fields like technical AI safety, economics, and AI governance. If we want to know how agents can jointly learn to cooperate, opponent shaping is the natural starting formalism.

In this post, we unpack how opponent shaping works, starting from its initial, complex formulation and arriving at a variant — Advantage Alignment — that makes the principle clear and tractable. First, we’ll see how this mechanism allows symmetric, peer agents to learn cooperation Then, we’ll examine what happens when these agents face less-sophisticated opponents, building a bridge from symmetric cooperation to asymmetric influence. Finally, we’ll explore the ultimate asymmetric case—AI shaping human behaviour—to draw out implications for AI safety and strategy.

This leads to several conclusions about human-AI and AI-AI interactions—some more surprising than others. The major goal of this piece is not to flabbergast readers with counterintuitive results, or shift the needle on threat models per se (although, I’ll take it if I can get it); but to re-ground existing threat models. The formalisms we discuss here are analytically tractable, computationally cheap and experimentally viable right now. They have been published for a while now, but not exploited much, so they seem to me under-regarded means of analyzing coordination problems, and they suggest promising research directions.

Opponent Shaping 1: Origins

I assume the reader has a passing familiarity with game theory and with reinforcement learning. If not, check out the Game Theory appendix and the Reinforcement Learning Appendix. Their unification into Multi-Agent Reinforcement Learning is also recommended.

In modern reinforcement learning, an agent’s strategy is called its policy, typically denoted $\pi$. Think of the policy as the agent’s brain; it’s a function that takes the current state of the game and decides which action to take. For anything but the simplest problems, this policy is a neural network defined by a large set of parameters (or weights), which we’ll call $\theta$. The agent learns by trying to maximize its expected long-term reward, which we call the value function, $V$.

It’s going to get tedious talking about “this agent” and “this agent’s opponent”, so hereafter, I will impersonate an agent (hello, you can call me Dan) and my opponent will be Alice.

I learn by adjusting my parameters using the policy gradient method. This involves making incremental updates to my parameters, ${\theta }^{\text{Dan}}$, to maximize my value (i.e., my long-term expected reward). As a standard, “naïve” learning agent I am only concerned with my own policy parameters and my own rewards. My opponent is a static part of the environment. The standard policy gradient is just

${\nabla }_{{\theta }^{\text{Dan}}}{V}^{\text{Dan}}$.

I’m not doing anything clever regarding Alice; I am treating her as basically a natural phenomenon whose behaviour I can learn but not influence.

Let’s see what happens when we add a “theory of mind” to the mix. The first method to do this was Learning with Opponent-Learning Awareness (LOLA), introduced in Jakob Foerster, Chen, et al. (2018). As a LOLA agent, in contrast to a naïve learner, I ask a more reflective question: “If I take this action now, how will it change what my opponent learns on their next turn, and how will that change ultimately affect me in the long run?”

I want to model the opponent not as a Markov process, but as a learning process. To formalize this in LOLA I imagine Alice taking a single, naïve policy-gradient update step. I then optimize my own policy to maximize my return after Alice has made that anticipated update to her policy.

Mathematically, this leads to an update rule containing the usual policy gradient term plus a clever—but complex—correction term. Foerster et al. show that by modelling the opponent’s learning step, the gradient for my policy, , should be adjusted by a term involving a cross-Hessian:

${\nabla }_{{\theta }^{\text{Dan}}}{V}^{\text{Dan}}+\beta \underset{\text{cross-Hessian}}{\underset{}{{\nabla }_{{\theta }^{\text{Dan}}}{\nabla }_{{\theta }^{\text{Alice}}}{V}^{\text{Dan}}}}{\nabla }_{{\theta }^{\text{Alice}}}{V}^{\text{Alice}}.$

The first term is the vanilla REINFORCE/actor-critic gradient. That second term is the LOLA formalization of learning awareness. It captures how tweaking my policy (${\theta }^{\text{Dan}}$) influences the direction of Alice’s next learning step (${\nabla }_{{\theta }^{\text{Alice}}}{V}^{\text{Alice}}$), and how that anticipated change in her behaviour feeds back to affect my own long-term value ($V^{\text{Dan}}$).

The Good News: This works.

Iterated Prisoner’s Dilemma: Two LOLA agents learn tit-for-tat–like cooperation, while independent learners converge to mutual defection.Robustness: In tournaments, LOLA successfully shapes most opponents into more cooperative play.

The Bad News: Stuff breaks.

That cross-Hessian term, ${\nabla }_{{\theta }^{\text{Dan}}}{\nabla }_{{\theta }^{\text{Alice}}}{V}^{\text{Dan}}$, is the source of major frictions:

Computational Nightmare: Calculating or even approximating this matrix of second-order derivatives is astronomically expensive for any non-trivial neural network policy.High Variance: Estimating second-order gradients from sampled game trajectories is an order of magnitude noisier than estimating first-order gradients, leading to unstable and fragile training.Complex Estimators: Making LOLA tractable required inventing a whole separate, sophisticated Monte Carlo gradient estimator algorithm (Jakob Foerster, Farquhar, et al. 2018) which is super cool but signals that the original approach was not for the faint of heart.Implausible transparency: AFAICT, as an agent, I need to see my opponent’s entire parameter vector, , which is an implausible degree of transparency for most interesting problems^[4].

So, LOLA provides a model—differentiate through the opponent’s learning—but leaves us unsatisfied. To escape this trap, researchers needed to find a way to capture the same signal without the mess of the Hessian, and the inconvenient assumptions.

Opponent Shaping 2: Advantage Alignment

The key to simplifying LOLA’s Hessian-based approach is a standard but powerful concept from the reinforcement learning toolkit: the advantage function. It captures the value of a specific choice by answering the question: “How much better or worse was taking action $a$ compared to the average value of being in state $s$?”

Formally, it’s the difference between the Action-Value ($Q^{\pi }(s,a)$, the value of taking action $a$) and the State-Value ($V^{\pi }\left(s\right)$, the average value of the state).

$A(s,a)=Q(s,a)-V\left(s\right).$

A key simplification came from Duque et al. (2024), who introduced Advantage Alignment at ICLR 2025, showing that the entire complex machinery of LOLA could be distilled into a simple, elegant mechanism based on the advantage function.^[5]

Their key result (Theorem 1 in the paper) shows that, under some reasonable assumptions, differentiating through the opponent’s learning step is equivalent to weighting my own policy update by a term that captures our shared history. Intuitively, this means: When our shared history has been good for me, I should reinforce my actions that are also good for her. When our history has been bad for me, I should punish my actions that are good for her.

Let’s see how this refines the learning rule. My standard policy gradient update is driven by my own advantage, $A^{\text{Dan}}$:

${\nabla }_{{\theta }^{\text{Dan}}}{V}^{\text{Dan}}=E[{\sum }_{t=0}^{\infty }{\gamma }^t{A}_t^{\text{Dan}}{\nabla }_{{\theta }^{\text{Dan}}}\log {\pi }^{\text{Dan}}(a_t\mid s_t)].$

Advantage Alignment modifies this by replacing my raw advantage with an effective advantage, , that incorporates Alice’s “perspective”.⁷ This new advantage is simply my own, plus an alignment term:

$A_t^{\ast }=\underset{\text{My own advantage}}{\underset{}{A_t^{\text{Dan}}}}+\beta \gamma \underset{\text{My cumulative past advantage}}{\underset{}{({\sum }_{k<t}{\gamma }^{t-k}{A}_k^{\text{Dan}})}}\underset{\text{Alice's current advantage}}{\underset{}{A_t^{\text{Alice}}}}.$

The update rule retains a simple form, but now uses this richer, learning-aware signal:

${\nabla }_{{\theta }^{\text{Dan}}}{V}^{\text{Dan}}=E[{\sum }_{t=0}^{\infty }{\gamma }^t{A}_t^{\ast }{\nabla }_{{\theta }^{\text{Dan}}}\log {\pi }^{\text{Dan}}(a_t\mid s_t)].$

We achieve the same learning-aware behaviour as LOLA, but the implementation is first-order. We’ve replaced a fragile, expensive cross-Hessian calculation with a simple multiplication of values we were likely already tracking in an actor-critic setup. This, for me, is what makes the opponent-shaping principle truly comprehensible and useful.

Note the bonus feature that we have dropped the radical transparency assumption of LOLA; I no longer need to know the exact parameters of Alice’s model, ${\theta }^{\text{Alice}}$.

3.Where does $A_t^{\text{Alice}}$come from?

In implementation (as per Algorithm 1), I, as the agent Dan, maintain a separate critic for my opponent Alice. I…

…collect trajectories under the joint policy $({\pi }^{\text{Dan}},{\pi }^{\text{Alice}})$.…fit Alice’s critic by Temporal-Difference (TD) learning on her rewards $r^{\text{Alice}}$ to learn$Q^{\text{Alice}}$ and $V^{\text{Alice}}$. (See the Reinforcement Learning Appendix for nitty-gritty).…compute $A_t^{\text{Alice}}=Q^{\text{Alice}}(s_t,a_t,b_t)-V^{\text{Alice}}\left(s_t\right)$in exactly the same way I do for myself.…plug that into the “alignment” term.

The Benefit

The final update rule for me then, as an AA agent is just the standard policy gradient equation, but with this learning-aware advantage signal:

${\nabla }_{{\theta }^{\text{Dan}}}{V}^{\text{Dan}}=E[A_t^{\star }{\nabla }_{{\theta }^{\text{Dan}}}\log {\pi }^{\text{Dan}}(a_t\mid s_t)]$

I get the benefit of opponent shaping without needing to compute any Hessians or other second-order derivatives.

This makes the principle tractable and the implementation clean.

Alice and I can master Prisoner’s Dilemma.

Time to go forth and do crimes!

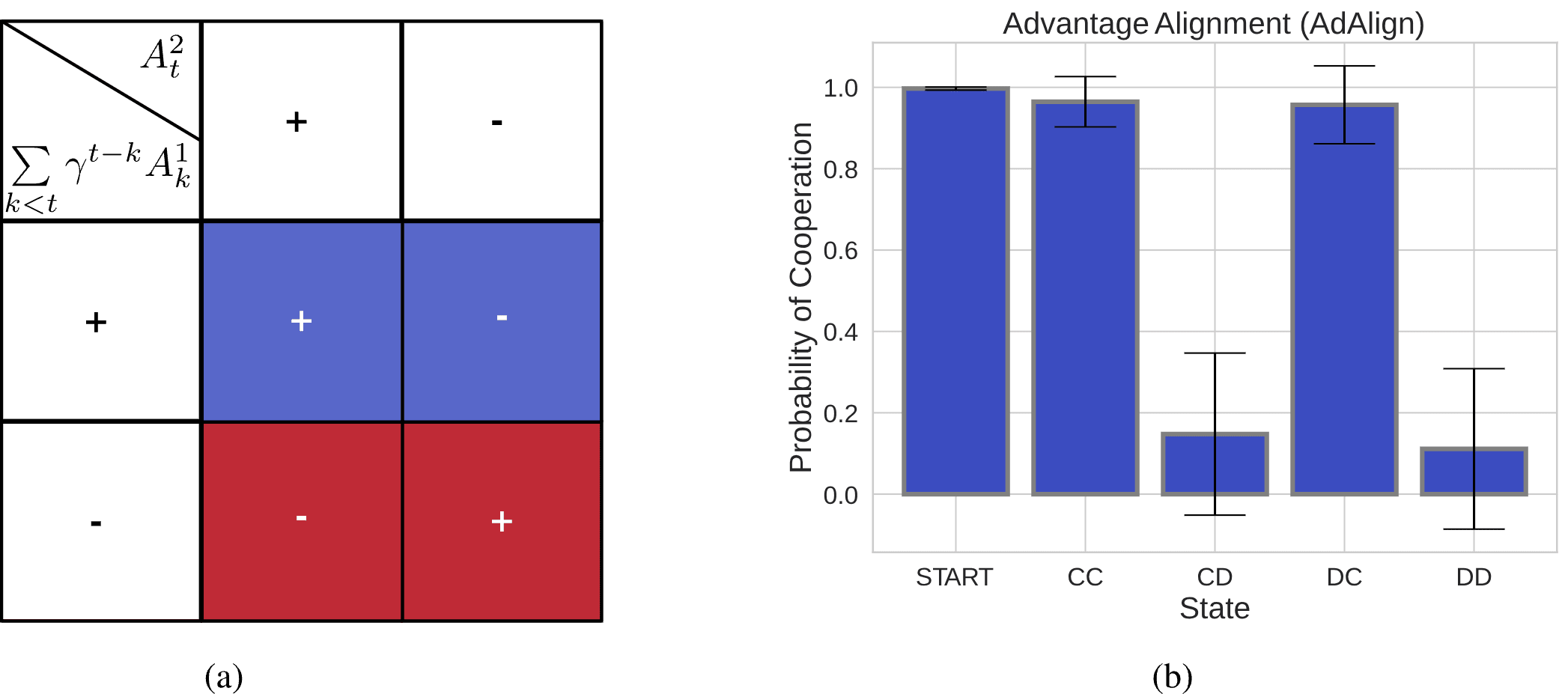
“The sign of the product of the gamma-discounted past advantages for the agent, and the current advantage of the opponent, indicates whether the probability of taking an action should increase or decrease.”“The empirical probability of cooperation of Advantage Alignment for each previous combination of actions in the one step history Iterated Prisoner’s Dilemma, closely resembles tit-for-tat. Results are averaged over 10 random seeds, the black whiskers show one std.”

Fig 1 from Duque et al. (2024) shows us learning Tit-for-tat, as we’d hoped.

The Price

Advantage alignment has a few technical assumptions required to make it go.

Agents learn to maximize their value functionAgents’ opponents select actions via a softmax policy based on their action-value function.

These assumptions hold for the most common architectures of RL agent, choosing to play softmax-optimal moves, but they are not universal.

Note also that we have smuggled in some transparency assumptions; The game must be fully-observed and I must see my opponent’s actual rewards () if I plan to estimate her value function, and vice versa. Further, I must estimate their advantage function, with sufficient fidelity to be able to estimate their updates. We don’t really get a formal notion of sufficient fidelity in the paper; though experimental results suggest it is “robust” in some sense

We could look at that constraint from the other side, and say that this means that I can handle opponents that are “approximately as capable as me”.

This might break down. I cannot easily test my assumption that my estimate of Alice’s value function is accurate. Maybe her advantage function is more computationally sophisticated, or has access to devious side information? Maybe Alice is using a substantially more powerful algorithm than I presume? More on that later.

Scaling up

Another hurdle we want to track is the computational cost, especially as the number of agents ($N$) grows. A naive implementation where each agent maintains an independent model of every other agent would lead to costs between all agents that scale quadratically ($O\left(N^2\right)$), which is intractable eventually.

Whether we need to pay that cost depends on what we want to use this as a model for. Modern MARL can avoid the quadratic costs in some settings this by distinguishing between an offline, centralized training phase and an online execution phase. The expensive part—learning the critics—is done offline, where techniques like centralised training with parameter sharing, graph/mean-field factorisations and Centralized-Training-for-Decentralized-Executions pipelines” (see Yang et al. (2018) on Mean-Field RL; Amato (2024) for a CTDE survey); those collapse the training-time complexity to roughly $O\left(N\right)$ at the price of some additional assumptions.

Scaling cost. If each agent naïvely maintained an independent advantage estimator for every other agent the parameter count would indeed be $O\left(N^2\right)$. At execution-time the policy network is fixed, so per-step compute is constant in $N$ unless the agent continues to adapt online.

Training vs. execution. The extra critics (ours and each opponents’) are needed at training time. If we are happy to give up online learning, then our policy pays zero inference-time overhead. If the we keep learning online there is an $O\left(N\right)$ cost for recomputing the opponent-advantage term, per agents. Shared critics or mean-field approximations can keep this linear in the lab for self-play.

Setting	Training-time compute	Per-step compute	Sample complexity	Typical tricks	Relevant?
Offline, self-play (symmetric)	$O\left(N\right)$(shared critic)	constant	moderate	parameter sharing	lab experiments
Offline, heterogeneous opponents	$O\left(N\right)$for $K$ opponent archetypes	constant	high	clustering, population-based training	benchmark suites
Online, continual adaptation	$O\left(N\right)$ per update	$O\left(N\right)$ if you recompute online	very high	mean-field, belief compression	most “in-the-wild” AIs
Large-N anonymous populations	$O\left(1\right)$(mean-field gradient)	$O\left(1\right)$	moderate	mean-field actor–critic	smart-cities / markets

Worked example

In the original blog post I inserted a worked example at this point, but it will be tedious to convert all that math from my blog and I do not wish to spend hours retyping, you will need to go to my blog to watch me struggle with entry-level calculus, if that kind of thing floats your boat. It’s fun. We solve for cooperate in IPD.

What did all that get us?

OK time to tease out what we can and cannot gain from this Opponent-shaping model.

Opponent-shapers are catalysts

The self-play examples show how peer agents can find cooperation. But the real world is messy, filled with agents of varying capabilities. I’m interested in seeing if we can push the Opponent Shaping framework to inform us about asymmetric interactions.

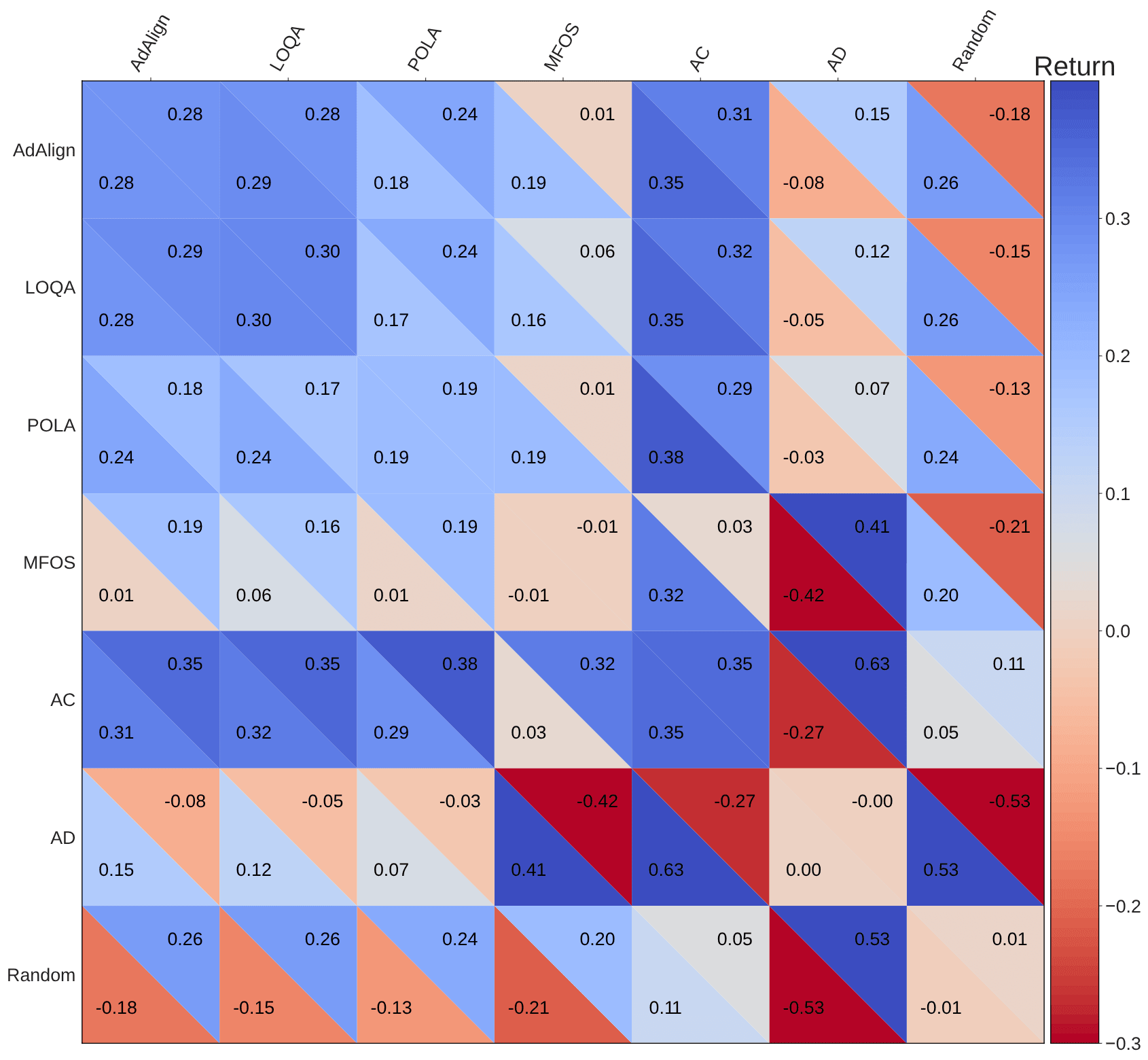
League Results of the Advantage Alignment agents in Coin Game: LOQA, POLA, MFOS, Always Cooperate (AC), Always Defect (AD), Random and Advantage Alignment (AdAlign). Each number in the plot is computed by running 10 random seeds of each agent head to head with 10 seeds of another for 50 episodes of length 16 and averaging the rewards. (Fig 2 from Duque et al. (2024))

 

The authors of both LOLA and Advantage Alignment tested this by running tournaments of the Opponent-Shaping-learned policy against a “zoo” of different algorithms, including simpler, naïve learners and other LOLA-like learners. What we discover is that LOLA is effective at steering other agents toward pro-social cooperation, even naïve ones. If we inspect the tournament matrix above (which is for a slightly different tournament game, the “coin game”) we can see this.
Read along the top row there— in each game we see the average reward earned by players playing two different strategies. The bottom-left is what the Advantage Aligned player earned each time, and the top right, what its opponent earned. For any non-angel (always cooperate) opponent, they benefited by playing against an advantage-aligned agent. Which is to say, if Alice is an advantage-aligned agent, I want to be playing against her, because she will guide us both to a mutually beneficial outcome. The deal is pretty good even as a “pure-evil” always-defect agent, or a random agent.I “want” to play against AA agents like Alice in the meta-game where we choose opponents, because Alice, even acting selfishly, will make us both better off. If Alice is an advantage-aligned agent, I want to be playing against her, because she will guide us both to a mutually beneficial outcome. The deal is pretty good even as a “pure-evil” always-defect agent, or a random agent. I “want” to play against AA agents like Alice in the meta-game where we choose opponents, because Alice, even acting selfishly, will make us both better off.

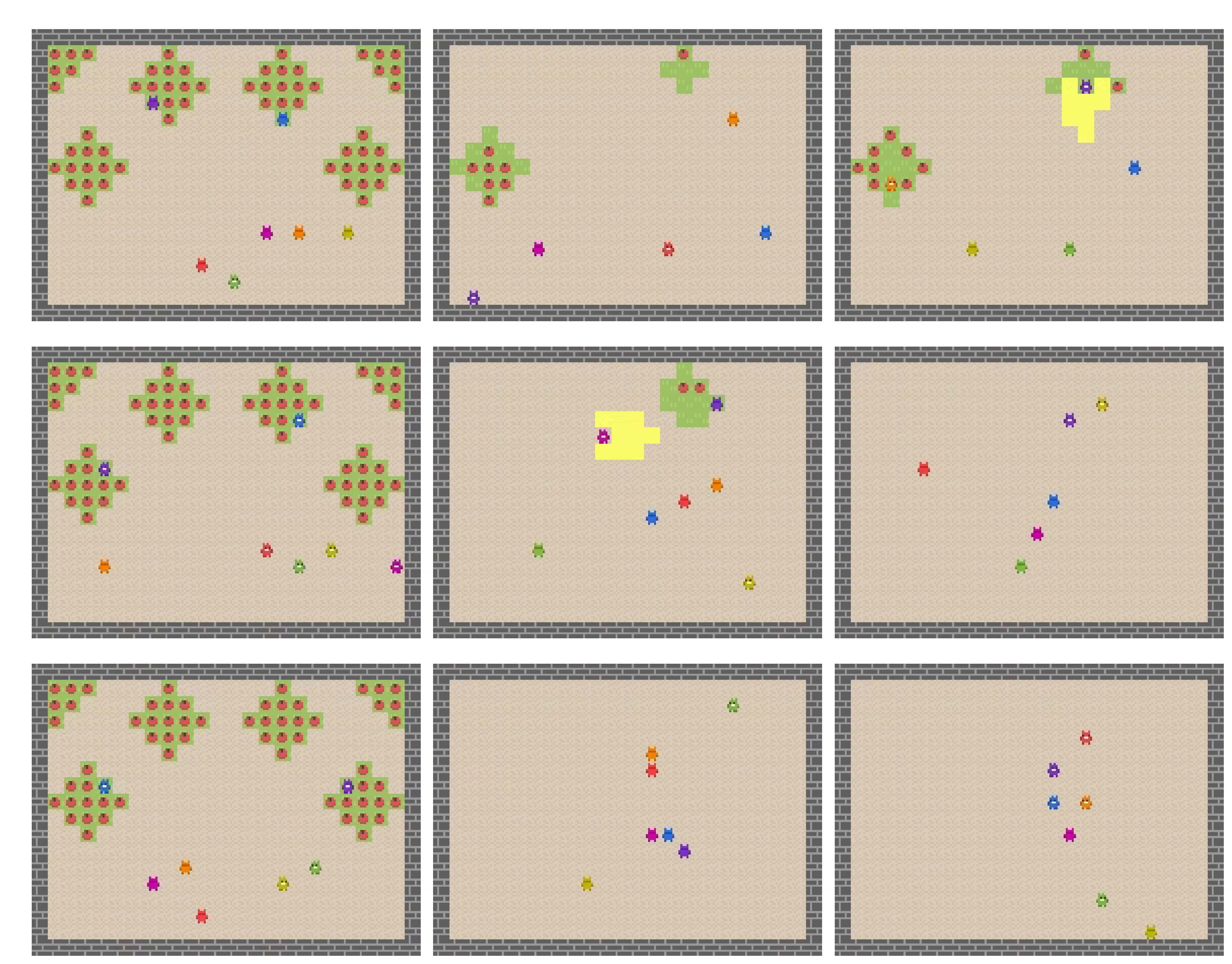
They scale this up to larger games, in the sense of multi-player games. The next figure shows scenes from a common-pool resource exploitation game, wherein two opponent-shaping agents are able to encourage five other agents to preserve a common-pool resource subject to over-harvesting, to everyone’s benefit. And just like that, we’ve solved sustainability!

Frames of evaluation trajectories for different algorithms. Qualitatively, we demonstrate that Proximal Advantage Alignment (AdAlign, top) also outperforms naïve PPO (ppo) and PPO with summed rewards on the next two rows. The evaluation trajectories show how AdAlign agents are able to maintain a bigger number of apple bushes from extinction (2) for a longer time that either ppo or ppo p. Note that in the Commons Harvest evaluation two exploiter agents, green and yellow, play against a focal population of 5 copies of the evaluated algorithm. (Fig 5 from Duque et al. (2024))

I find this generally a mildly hopeful message for understanding and generating cooperation in general. Nation-states and businesses and other such entities all have a kind of learning awareness that we might model as “opponent-shaping”. Insofar as their interactions are approximately symmetric and the other assumptions are satisfied (consistency over time, etc) we can hope that nation-states might be able to achieve positive interactions in pairwise interactions.

Although, that said, with Actor-critic methods and small gradient updates it might take a few million interactions to learn the cooperating policies, so you don’t want to rely this in the real world, necessarily.

There is a more reassuring message here though: The strategic calculus of peer agents can potentially produce stable cooperation. The “arms race” of “I’m modelling you modelling me…” appears to be short; the original LOLA paper (Jakob Foerster, Chen, et al. 2018) found that a 2nd-order agent gained no significant advantage over a 1st-order one in self-play. We can interpret this in terms of strategic logic as follows:

The cost of escalation is immense.The risk of effective retaliation is high.The probability of gaining a lasting, decisive edge is low.

The rational course of action is therefore not to attempt domination, but to secure a stable, predictable outcome. This leads to a form of AI Diplomacy, where the most stable result is a “Mutually Assured Shaping” equilibrium.

Asymmetric capabilities: Are humans opponent shapers, empirically?

Sometimes? Maybe? It seems like we can be when we work hard at it. But there is evidence that we ain’t good at being such shapers in the lab.

The Advantage Alignment paper admits asymmetric capabilities in its agents, but does not analyze such configurations in any depth. AFAIK, no one has tested Opponent Shaping policies against human by that name. However, we do have a paper which comes within spitting distance of it. The work by Dezfouli, Nock, and Dayan (2020)^[6] trains RL agents to control “surrogate” humans, since real humans are not amenable to running millions of training iterations. They instead set up some trials with human in a lab setting, and trained an RNN to ape human learning in various “choose the button” experiments. This infinitely patient RNN will subject itself to a punishing round of RL updates. 

The goal of that paper is to learn to train RL agents to steer the humans with which they interact. The remarkable result of that paper is that RL policies learned on the surrogate humans transfer back to real humans. The adversary in those settings was highly effective at guiding human behaviour and developed non-intuitive strategies, such as strategically “burning” rewards to hide its manipulative intent.^[7]

Against a sufficiently powerful RL agent, humans can be modelled as weaker learners, for one of several reasons.

Modelling Capability: An AI can leverage vast neural architectures to create a high-fidelity behavioural model of a human, whereas a human’s mental model of the AI will be far simpler.Computational Effort: An AI can run millions of simulated interactions against its model to discover non-intuitive, effective policies. A human cannot, and often lacks the time or enthusiasm to consciously model every instance of digital operant conditioning they face daily.Interaction History: While the formalism only requires interaction data, an AI can process and find patterns in a vast history of interactions far more effectively than a human can.

The Dezfouli, Nock, and Dayan (2020) experiment demonstrated that this asymmetry could be readily exploited. One is that the asymmetric shaping capability is not necessarily mutually beneficial. Trained to exploit the naïve learner, this policy can find beneficial or indeed exploitative equilibria. A MAX adversary with a selfish objective learned to build and betray trust for profit, while a FAIR adversary with a prosocial objective successfully guided human players toward equitable outcomes. I don’t want to push the results of that paper too far here, not until I’ve done it over in an opponent-shaping framework for real. However we should not expect Opponent-shaping agents to be less effective than the naïve algorithm of Dezfouli, Nock, and Dayan (2020) at shaping the behaviour of humans.

The implications in that case are troubling both for humans in particular, and asymmetric interactions in general.

Unknown capabilities

OK, we did equally-capable agents, which leads to a virtuous outcome, and asymmetric agents which leads to a potentially exploitative outcome.

There is another case of interest, which is when it is ambiguous what the capabilities of two opponents are. This is probably dangerous. A catastrophic failure mode could arise if one agent miscalculates its advantage and attempts an exploitative strategy against an opponent it falsely believes to be significantly weaker, triggering a costly, destructive conflict. This creates a perverse incentive for strategic sandbagging, where it may be rational for an agent to misrepresent its capabilities as weaker than they are, luring a near-peer into a devastatingly misjudged escalation. True stability, therefore, may depend not just on raw capability, but on the ability of powerful agents to credibly signal their strength and avoid such miscalculations.

Scaling Opponent Shaping to many agents

OK, we have some mild hope about cooperation in adversarial settings in this model.

Let us leaven that optimism with qualms about scalability. This mechanism of implicit, pairwise reciprocity will face problems scaling up. We can get surprisingly good cooperation from this method, but I would be surprised if it were sufficient for all kinds of multipolar coordination.

Even in a setting such as no-online learning where the training cost for each of our per-agent is a manageable $O\left(N\right)$ and execution is constant (i.e. we are not learning from additional experience “in the wild”), the sample complexity—the total amount of experience needed to learn effective reciprocity with all other agents—grows significantly. Furthermore, the communication overhead (i.e. interaction history) required to maintain these pairwise relationships we can imagine becoming a bottleneck for complicated interactions. ^[8] We suspect this becomes intractable for coordinating large groups.^[9]

Even with linear training-time scaling, sample inefficiency and coordination overhead likely swamp pairwise reciprocity once grows large; this, rather than per-step compute, motivates institutions—laws, markets, social norms—that supply cheap global coordination. These are mechanisms of cooperative game theory, designed to overcome the scaling limits of pairwise reciprocity by establishing explicit, enforceable rules and shared infrastructure.

Takeaways: Grounding strategic risk, and other uses for this formalism

The strategic landscape of AGI is often discussed in terms of intuitive but sometimes imprecise concepts. We talk about treacherous turns, manipulation, and collusion without always having a clear, mechanistic model of how these behaviors would be learned or executed. The primary value of the opponent shaping framework is that it provides precisely this: a minimal, tractable, and empirically testable formalism for grounding these intuitions, and some logical next experiments to perform.

The key takeaways are not the risks themselves—which are already in the zeitgeist—but how opponent shaping allows us to model them with new clarity.

From “Manipulation” to Computable Asymmetry.

The risk of an AI manipulating its human operators is a core safety concern. Opponent shaping translates this abstract fear of being ‘reward hacked’ (i.e., steered into preferences that benefits the AI at the human’s expense) into a concrete, measurable quantity. The opponent-shaping framework gives us two ‘knobs’ to model this asymmetry: the explicit shaping parameter (), which controls how much an agent cares about influencing the opponent, and the implicit fidelity of its opponent model. An agent with a superior ability to estimate its opponent’s advantage () can achieve more effective shaping, even with the same . This turns the abstract fear of manipulation into a testable model of informational and computational asymmetry. From here we can re-examine proof-of-concept papers like Dezfouli, Nock, and Dayan (2020) with more tuneable theory of mind. What do the strategies of RL agents, armed with a basic behavioural model, look like as we crank up the computational asymmetries? Opponent shaping allows us to start modelling asymmetry in terms of a learnable policies.

Treacherous turns

The concept of a treacherous turn—an AI behaving cooperatively during training only to defect upon deployment—is often framed as a problem of deception. Opponent shaping is an interesting way to model this, as the optimal long-term policy for a self-interested agent with a long time horizon ($\gamma$ close to 1). The investment phase of building trust by rewarding a naïve opponent is simply the early part of a single, coherent strategy whose terminal phase is exploitation. This temporal logic is captured by the alignment term, $\beta \gamma ({\sum }_{k<t}...)A_t^{\text{opponent}}$, in the effective advantage update. This allows us to analyze the conditions (e.g., discount factors, observability) under which a treacherous turn becomes the default, profit-maximizing strategy, although let us file that under “future work” for now.

AI Diplomacy

We speculate about how powerful AIs might interact, using analogies from international relations. The opponent shaping literature, particularly the finding that the 2nd-order vs 1st-order LOLA arms race is short, provides a formal basis for AI-AI stability. It suggests that a “Mutually Assured Shaping” equilibrium is a likely outcome for peer agents. This is not based on altruism, but on the cold calculus that the expected return from attempting to dominate a fellow shaper is negative. This provides a mechanistic model for deterrence that doesn’t rely on analogy. It also allows us some interesting hypotheses, for example: a catastrophic conflict is most likely not from pure malice, but from a miscalculation of capabilities in a near-peer scenario, leading to a failed attempt at exploitation.

From Scalable Oversight to Institutional Design

The problem of managing a large population of AIs is often framed as a need for ‘scalable oversight.’ The quadratic complexity of pairwise opponent shaping gives this a computational justification. It formally demonstrates why pairwise reciprocity fails at scale and why designed institutions (mechanisms from cooperative game theory) are likely a computational necessity, at least in this competitive game-theory setting. It reframes the AI governance problem away from solely aligning individual agents and toward the distinct problem of designing the protocols, communication standards, and monitoring systems that constitute a safe multi-agent environment.

Next Steps

This has been a great learning exercise for me, and help me crystallise many half-formed ideas. My next steps are to apply this formalism to model specific strategic scenarios, such as the treacherous turn or multi-agent institutional design. Feel free to reach out if you want to take it somewhere.

Acknowledgements

Juan Duque graciously answered my questions about the Advantage Alignment.Seijin Kobayashi spent substantial time helping me understand Meulemans et al. (2024).Gemini Pro 2.5 expanded my dot points into drafts which I then completely rewrote because its prose is painful. It was much more effective at critiquing my document structure though — you can thank it for the appendices.ChatGPT o3 checked my mathematics

Appendices

No, I absolutely cannot be bothered retyping all the mathematics from my blog into lesswrong. You can read it in situ. You might enjoy it, there is a very dry joke about CartPole.

1. ^{^}

   The additional condition $2R>T+S$ is also common, ensuring that taking turns defecting isn’t better than consistently cooperating.

2. ^{^}

   I am committing an act of machine-learning chauvinism here for the sake of simplicity. If you include evolutionary learning as a learning algorithm, then much effort has been spent on modelling strategies in evolutionary game theory, starting with the notion of Evolutionarily Stable strategies (Smith and Price 1973).

3. ^{^}

   The name itself is something of a misnomer, suggesting pure conflict, but it applies equally to games where a cooperative outcome is attainable.

4. ^{^}

   The open-weight setting brings us to Open Source Game Theory Critch, Dennis, and Russell (2022), which is a distinct, though related, field

5. ^{^}

   There are many variants of LOLA that we are not expanding upon here; AFAICT Advantage Alignment is the first one to be substantially more comprehensible and practical, but I could have missed some

6. ^{^}

   This Dezfouli paper is IMO straight 🔥; I don’t know why it isn’t more frequently discussed.

7. ^{^}

   This is a fascinating result from the paper: to prevent the human from realizing they were being manipulated into a low-reward action, the AI would sometimes forego a high reward for itself on a different action, obscuring the pattern and keeping the human compliant for longer.

8. ^{^}

   In the wild, agents are likely not independent, but that is a whole other story, for a more elaborate formalism.↩︎

9. ^{^}

   There is another sense in which we expect this not to scale to massively multiplayer games such as the famed multi-polar-trap because the reward signal is too dilute, but that is a matter for a future post. Maybe start with the mean-field formulation of Yang et al. (2018).

Discuss