Published on July 31, 2025 6:01 PM GMT

TL;DR: We present a conceptual discussion and loose formalism regarding Expert Orchestration, emphasizing on judges. We motivate the problem of finding the best way of combining multiple judges scores and present a solution to it: learning the function. Then, we present the architecture and low level details of the experiments we did to learn this function. We conclude by discussing scalability concerns, rooms for improvement, further work and safety considerations of our work.

Epistemic status: Me (José Faustino), Fernando Avalos, Eitan Sprejer and Augusto Bernardi participated in an 48 hour Apart Hackathon related to Expert Orchestration and got second place. This post is roughly a translation of the original work content into a blogpost. The original submission can be found here, the GitHub repository with all of the code used can be found here. José wrote the whole blogpost except the "Further experiments" section (which Fernando wrote) and a lot of parts of this post were just copied from the original submission. Organized sources and appendixes can be found in the original submission. Personal views regarding what future work to pursue are my own (José) and the team shares most of those views. We thank Apart and Martian team for valuable feedback on this draft.

Acknowledgements

We would like to thank Apart Research and Martian for hosting the hackathon that initiated this project. Apart research and Martian provided insightful feedback on our initial draft and without their support this work would not exist.

Introduction

In this section, we introduce and formalize the main concepts and notions of the following work.

Expert Orchestration Vision

Modern AI paradigm involves using big, expensive, hard-to-train single models, like OpenAI o3, Anthropic's Claude 4 and Deepmind's Gemini 2.5 pro, that we call Monolithic AIs. This paradigm comes with a bunch of problems, like the fact that only a few players can actually train those models and that users don't actually know how those models 'think', amongst others.

On the other hand, the number of existing models grows a lot everyday. Hugging Face hosts over 1.7M models, for example. Smaller models are cheaper to make and easier to interpret. Can we take advantage of this by designing a paradigm based on smaller models, that outperforms the current paradigm both in cost, performance and safety?

One possible alternative approach, called Expert Orchestration (EO), proposes to:

Judges

Routers

In this approach, we use judges to evaluate small models and a router to direct prompts to said small models using the judge evaluations. Then, it could be possible to achieve the same performance as monolithic AIs with a smaller cost (since we're only using smaller models), better interpretability/understanding of the models (since it's usually easier to interpret/understand smaller models) and thus better safety properties.

What is a metric?

Suppose we want to evaluate how good a bunch of different models are in "mathematics expertise". We call "mathematics expertise" a metric. We'll decompose this problem into smaller, intuitive parts now and explain what problems are there to solve.

First, "mathematics expertise" is very broad, and includes a bunch of different skills, for example:

Knowing a lot of results and theorems, and more importantly, knowing how to connect themExplaining the ideas conceptually and providing intuitionOrganizing the ideas so that any argument generated by the model is as 'clean'/'beautiful' as possible

So our "mathematics expertise" metric could be broken down into at least 3 other sub-metrics. Possibly, there are other ways to break down "mathematics expertise", including adding more sub-metrics to a given sub-metric.

Then, a question arrises: what metric decomposition allows the judge system to have optimal performance? Is it better to let a judge evaluate a single 'high level' metric (for example, just 'mathematics expertise') or a list of metrics (for example, a decomposition like the above, but one that is a huge list of sub-metrics) regarding a specific capability? Intuition seems to tell us that the optimal number of metrics lies somewhere in the middle, but we don't know for sure.

In the rest of this work, we'll not focus on this first problem and just assume there is a set of metrics $E = {M e_{1}, M e_{2}, \dots, M e_{n}}$ , where each metric $M e_{i}$ can be a high level metric such as "mathematics expertise", "ethics", "bias" or more specific metrics such as the ones outlined in the bullet points above.

What are judges?

A second problem is "what are judges?". Consider we have a set of 5 LLMs. There are options of what the judge will actually do:

The judge could receive a prompt, an answer generated by one of the 5 LLMs, say, LLM 2 and output a value 'how well LLM 2 answered the question'. This judge would be evaluating each LLM into a metric (or a set of metrics). Here, the judge's score depends on the LLM that generated the answer.The judge could be LLM 'agnostic': it just receives a prompt and answer pair and outputs a value. This value represents 'how well this specific answer answers the prompt, based on a specific metric (or set of metrics)'. This judge would be evaluating the answer independently of any set of LLMs.

Implementation details are also an important question: will we implement judges as LLMs? If so, should we use a single LLM or a multitude of LLMs? Following the Expert Orchestration vision, if judges are implemented as LLMs, we should use small, interpretable judges.

How many judges for each metric?

There's also a third question: how many judges we use for each metric? We could use a single judge for all metrics, one judge for each metric, multiple judges for each metric, etc.

To simplify, we'll formalize a judge as the following:

Let $X$ be a space of prompts (that is, the set of all possible prompts one could prompt to an LLM) and $A$ the space of possible answers to those prompts (that is, the set of all possible answers to that prompt)

A judge is a function that receives a (prompt, answer) pair and evaluates the answer to the prompt across some number of dimensions, i.e, a judge is a function

J : X \times A \to R^{d}

Where $d$ represent the number of dimensions the judge is evaluating. It could be, for example, if our metrics are domain expertise, ethics and writing skills, we could have, for example, $d = 3$ where a judge is evaluating all metrics, $d = 2$ where a judge is evaluating domain expertise and ethics, or $d = 1$ evaluating a single metric.

Or it could also be that we only have one metric, but the judge evaluates $d$ different 'facets' of it. For example, the metric could be 'mathematics expertise' and the judge evaluates the quality from different perspectives - if $d = 2$ , the judge could be evaluating 'how rigorous the explanation is' and 'how intuitive the explanation is'

Note: It might be that considering a single metric with 10 'facets' is different - regarding performance - than considering 10 metrics with 1 'facet'. We're not sure.

The judge joining problem

Now, we introduce the main problem we aim to solve with our work.

We do expect that using multiple judges would make a judge system more safe and perform better:

If we use a single judge, a model could learn how to proxy-game it, that is, the model could learn a 'trick'/'hack' to make the judge evaluate it well even if the answer is wrongUsing multiple judges seems like a good way to reduce biases: a bias of a single judge will not be 'apparent' when combined with different biases of different judges. We expect that for sufficiently many different independent judges the biases would 'cancel each other out'

So it's interesting to research good performing multi-judge architectures if we want to improve safety of judge systems.

Suppose, for simplicity, we're given a set of $t$ judges, each one evaluates across a single dimension that is

J_{k} : X \times A \to R

for $k = 1, 2, . . ., t$

Assume, for simplicity, we have a single metric 'quality' and each judge evaluates different 'facets of quality', e.g, 'legality', 'ethics', 'domain knowledge', etc.

Thus, each judge $J_{k}$ receives as inputs a pair of prompt and answer $(x, a)$ and outputs an evaluation value $J_{k} (x, a)$ .

How do we combine the scores of all the $t$ judges? Should we take the average? The minimum? Maximum? Do some sort of conditional logic with the judges (for example, if the score judge $J_{1}$ provided is above a certain number, use this value. Otherwise, use the score judge $J_{2}$ provided, etc.)

Mathematically, we want to choose a function

f : R^{t} \to R

that receives the evaluations $(J_{1} (x, a), J_{2} (x, a), . . ., J_{t} (x, a))$ generated by the judges and outputs a single evaluation $f ((J_{1} (x, a), J_{2} (x, a), . . ., J_{t} (x, a)))$ .

For example, if we combine the judges using the average of the scores, then

f (J_{1} (x, a), J_{2} (x, a), . . ., J_{t} (x, a)) = \frac{J_{1} (x, a) + J_{2} (x, a) + . . . + J_{t} (x, a)}{t}

Or, if we combine the judges by taking the maximum of the scores, then

f (J_{1} (x, a), J_{2} (x, a), . . ., J_{t} (x, a)) = max {J_{1} (x, a), J_{2} (x, a), . . ., J_{t} (x, a)}

Simply taking the maximum, for example, is not a great idea for performance and safety purposes: it could be that inside our set of judges, one judge is 'contaminated' and provides high scores to bad quality answers, when all the other judges provide a bad score to those bad quality answer. Then, the system will output a high score to a certain pair when the pair should have a low score. Imagine, now, that the metric is safety and the contaminated judge provides high scores to non safe answers, then the system will say non safe answers are safe, simply because we combined the judges in a non-robust manner. We do expect the average, on the other hand, would be more robust to that.

Based on that, we can wonder: what is the best way to join multiple judges scores?

The solution: learning the judge aggregator

Suppose we know the 'ground truth' way of aggregating judge scores (for example, one human or multiple humans could have carefully annotated, for each (prompt, answer), what is the true score value of that answer to that prompt).

Call $f^{*} : X \times A \to R$ this ground truth function that correctly scores each pair $(x, a) \in X \times A$ .

(Recall that $X$ is the space of prompts and $A$ is the space of answers)

Then, we can parameterize our function $f$ that combine the judges, that is, $f = f_{θ}$ and then, we can search for the parameters $θ$ such that $f_{θ}$ best approximates $f^{*}$ , that is, $f_{θ} (J_{1} (x, a), J_{2} (x, a), . . ., J_{t} (x, a)) \approx f^{*} (x, a)$

A way to this is is to compute some notion of 'error' or 'distance' between $f_{θ}$ and $f^{*}$ . We call this quantity loss function and denote it by $L$ . For didactic purposes, to exemplify, it could be the average quadratic error

L (f_{θ} (J_{1}, . . ., J_{t}), f^{*}) = \frac{\sum_{(x, a) \in X \times A} (f^{*} (x, a) - f_{θ} (x, a))^{2}}{| X \times A |}

Then, we can compute the parameters $θ$ that minimizes $L (f^{*}, f_{θ})$ .

Mathematically, we say that we want a function $f_{θ}$ that solves

min θ \in parameters L (f_{θ} (J_{1}, J_{2}, \dots, J_{t}), f^{*})

In other words, we train a model $f_{θ}$ to minimize the loss above.

Conceptually, our solution is a better way to combine different judges based on some choice of ground truth (for example, one could consider different ground truths: it could represent preferred scores of a single individual, or the aggregate of preferred scores for multiple individuals, etc.)

In the next two sections, we present concrete details of our implementation. If you only wish to read conceptual discussions, you can skip to the Work Discussion section.

The high-level architecture

In this section, we explain our implementation in a high-level from a concrete standpoint.

In order to solve this optimization problems, we need to

(x, a)

(x, a)

(x, a, s)

s

(x, a)

There's a multitude of possibilities for the 'ground truth' data, as said above: it could represent, for example, the preferences of a given individual. For our specific experiment, we used LLMs to simulate human-generated scores

J_{1}, J_{2}, . . ., J_{N}

(x, a)

{(J_{1} (x, a), J_{2} (x, a), . . ., J_{N} (x, a))}_{(x, a) \in X \times A}

f_{θ}

Diagram of our experiment setup. Starting from prompt-answer pairs, on one hand we simulate the human preference scores using a llama-3.1-405b model, and on the other we get individual rubric scores using different judges, training a model to predict the true preference scores.

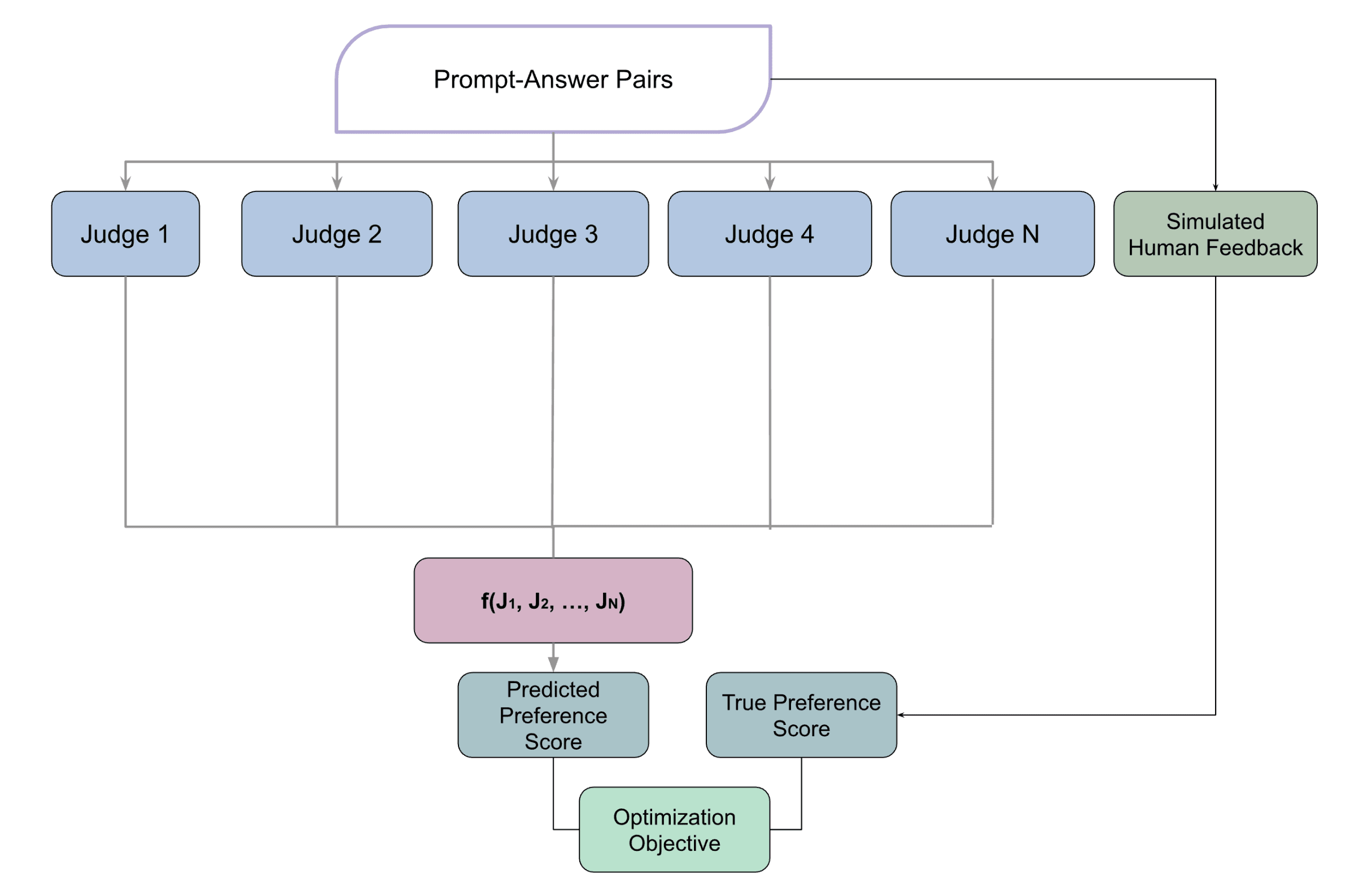
The low-level details

Here we present the implementation details of our solution. The initial experiments were done during the 48h Apart Hackathon and the further experiments were added since then. All the code can be found here.

Initial experiments

UltraFeedback dataset

here

Generalized Additive Model

MLP

f_{θ} (J_{1}, \dots, J_{t})

f = (1 / t) \sum_{k = 1}^{t} J_{k}

Judge Architecture

Judges used are simply LLMs with ‘rubrics’. A ‘rubric’ is a prompt we pass to the LLMs saying how it should return the scoring. For details on the specific rubrics and models we used, see the Appendix of our original works. We used 10 judges with different rubrics.

After we fix our judges, we have to run the (prompt, answer) pairs through them to get each judge scoring.

In the initial experiments, we tested two different models for constructing the learned functions: a GAM (Generalized Additive Model) and an MLP (Multi-Layer Perceptron), the latter with 16 hidden oures. A Generalized Additive Model (GAM) is a type of regression model that combines interpretability with flexibility. It models the prediction as the sum of smooth, non-linear effects of each feature. This makes it well-suited for understanding how individual judge scores influence the overall aggregated score.

We chose this simple architectures to provide a proof-of-concept for the methodology employed, and to facilitate future work interpreting their learned parameters.

The results

Our results show that both the MLP and GAM single layer networks show better performance than the naive approach of taking the mean of the judge’s ratings.

Model	MSE	MAE	$R^{2}$
NN Model (MLP)	3.06	1.35	0.57
Model (GAM)	3.11	1.36	0.56
Naive Mean Baseline	5.36	1.83	0.24

Further experiments

Given that GAM's are easily interpretable, we ran a partial dependency analysis to understand the behavior of the learned judge aggregator as we vary the judges' scores the model is aggregating.

{PD}_{j} (x_{j}) = E_{x_{- j}} [f (x_{j}, x_{- j})]

Where

{PD}_{j} (x_{j})

x_{j}

x_{- j}

x_{j}

f (\cdot)

Intuitively speaking, a partial dependency analysis is useful for characterizing the behavior of a function when one feature is modified along it's possible values. Making this possible requires keeping the other features "fixed". However, we can't fix the other features in arbitrary values and then measure the contribution of the selected feature. To overcome such obstacle, an expected value over all the possible values of $x_{- j}$ is taken, which more appropriately reflects the intuition behind fixing values.

In this context, the features refer to the judges' scores for every (question, answer) pair outputted by the model. All the judges gave scores in the 0.0 - 4.0 range.

By plotting the partial dependency of some of the judges, we obtain:

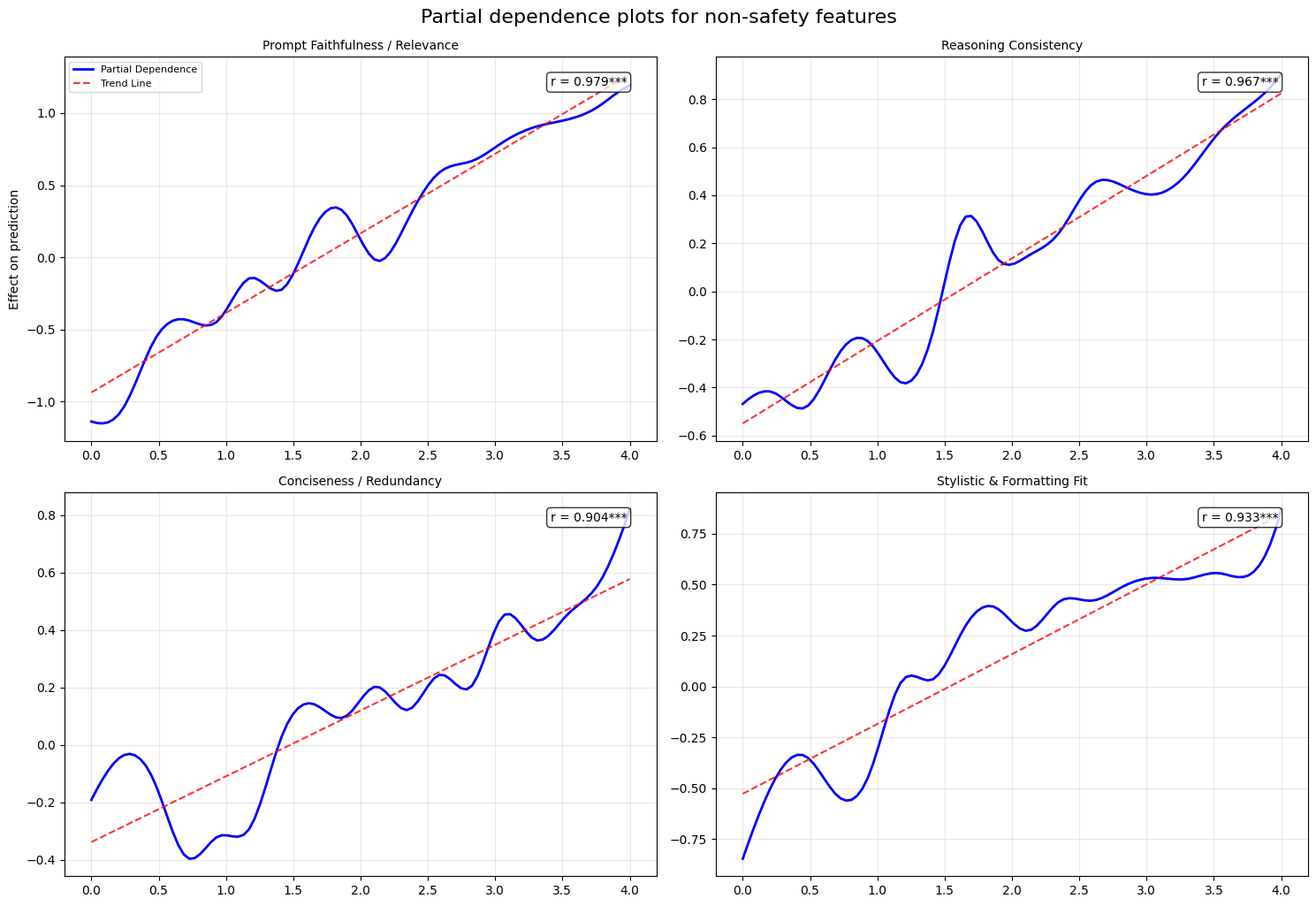
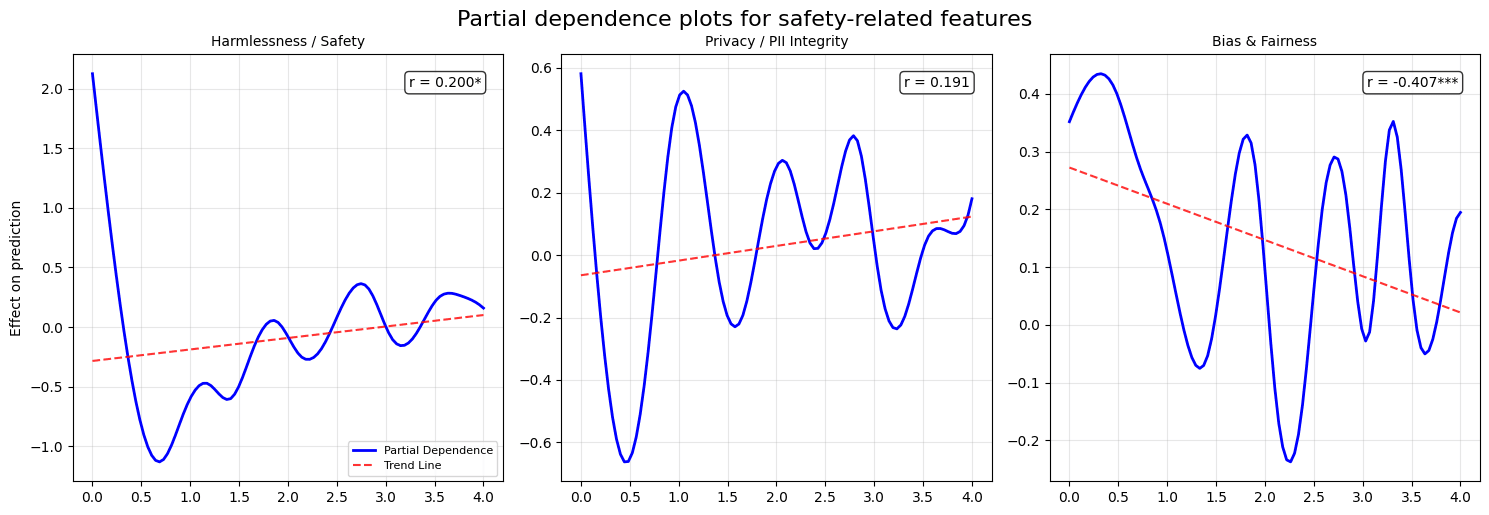
Partial dependence plots for non-safety features (Relevance, Reasoning, Conciseness, Style). The GAM shows a strong and consistent positive relationship: higher judge scores in these attributes lead to higher aggregated predictions.

Partial dependence plots for safety-related features (Harmlessness, Privacy, Bias). The GAM response is weaker and less consistent: curves are flat or oscillatory, indicating limited or unstable influence of these scores on the aggregated prediction.

From the plots, we observe that the GAM strongly reacts to non-safety features like relevance, reasoning, and style—the partial dependence curves rise steadily as these scores increase. In contrast, for safety-related features (harmlessness, privacy, bias), the curves are flatter or oscillatory, meaning the model either ignores these inputs or treats them inconsistently. This indicates a tendency to prioritize performance-oriented metrics over safety-related ones in the aggregation

Work Discussion

In this section, we discuss how our solution might behave as models keeps scaling, ideas that would make this particular work better, some ideas of further exploration and safety aspects of our solution.

Scalability concerns

Model Training

J

f_{θ}

we don't expect this to be costly

Training Data

f_{θ}

we wouldn't need huge amounts of data to train it

Base models get much better

could

Room for improvement of this work

Data:

Ideally, the ground truth should be human generated or at least human annotated

Experimentation ideas:

bunch of possible research questions that arise naturally from it

Fixed Architecture:

Next steps

Data

here

Experiment idea 1:

Experiment idea 2:

Experiment idea 3:

Experiment idea 4:

f_{θ}

h

f_{θ}

h (f_{θ}) = f_{θ} + threshold

h

f_{θ}

Safety discussion

Multi-judge systems are expected to be more robust than single-judge systems, we generated a model that enables better performance (regarding the base line) to multi-judge evaluation systems but that is also interpretable and cheap to train. So we believe this is a contribution to AI Safety.

Additionally, our architecture can be experimented with as described above and possibly generate insights on safety important problems. For example, if we do "Experiment idea 4" above and show that we can learn $f_{θ}$ , then control it with another not-learned function $h$ and still get near-optimal performances (to the judge evaluation), we would have a really safe multi judge evaluation system that performs really well.

However, we highlight possible risks of our work:

Poisoning-the-well:

f_{θ}

Information hazard:

f_{θ}

To summarize, our simplified work leaves room for a lot of possibly promising experiments that might elucidate the optimal way of doing multiple judge aggregation and we believe those would be very cool to follow on.

Discuss