Published on July 29, 2025 1:10 AM GMT
Abstract
The Fermi Paradox questions the absence of observable advanced civilizations in a vast universe. This proof resolves it using two verified physical limits: Landauer's principle (minimum energy for information erasure) and the Bekenstein bound (maximum information density). Any progressing civilization (effective information growth r > 1) reaches an informational singularity in finite time, transitioning to silent computational black holes. Given today’s global data volume (~181 ZB [7]) and a minimal loss-free growth rate (golden ratio φ ≈ 1.618), the threshold arrives in ≈ 192 years. Derived mathematically, verified in Lean4, the proof shows silence as physical necessity. Model robust to variations, consistent with recent JWST observations.
Executive Summary
Key idea. Advanced civilizations disappear from view not by dying out, but by collapsing into ultra-compact, information-dense objects. Silence is not a choice, but a physical inevitability.
Why it is inevitable.
Erasing information demands energy (Landauer’s principle [1–3]).
Storing information faces a finite surface-area limit (Bekenstein bound [4]).
Any culture with net positive information growth (r > 1) therefore hits that limit in finite time.
What happens next. Exceeding the information-density bound forces civilizations to concentrate mass-energy, triggering gravitational collapse into black holes. An illustrative φ-baseline places humanity ~192 years from the threshold, but code lets readers explore any parameters.
Quantitative Forecast (Illustrative)
| Scenario | Annual Growth (r) | Years Until Singularity | Year Reached |
|---|---|---|---|
| Conservative (23% annual) | 1.23 | 446 | 2471 |
| Big-Data (40% annual) | 1.40 | 275 | 2300 |
| φ Baseline (Minimal Lossless) | 1.618 | 192 | 2217 |
The φ-scenario yields t ≈ 191.8 years. We round this up to 192 for conservatism. Python verification confirms 2217 (2025 + ceil 191.8).
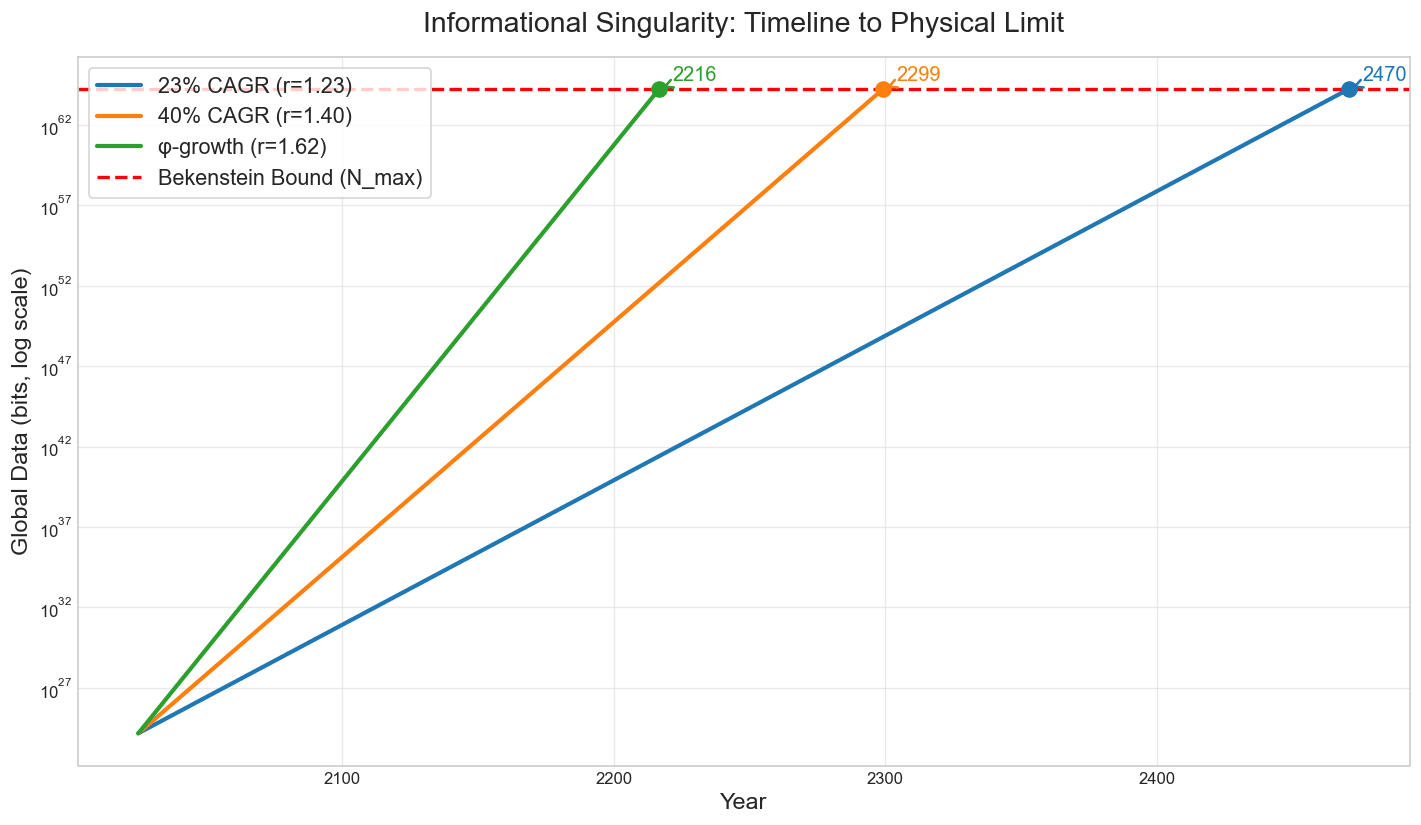
Figure 1 — Exponential data-growth curves (log scale) intersect the finite Bekenstein bound. The φ-trajectory crosses at 2217 CE. Conservative and big-data scenarios follow.
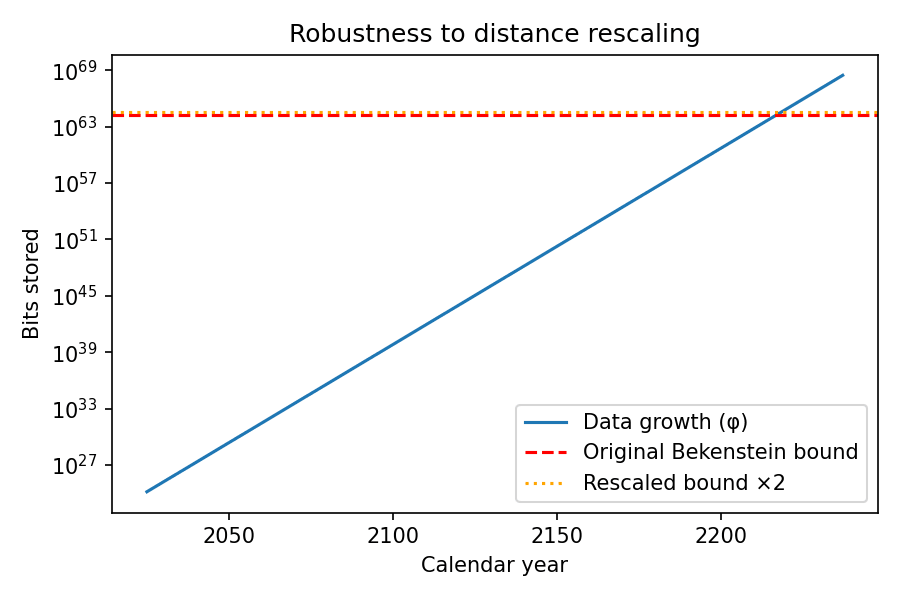
Figure 2 — Doubling the information bound delays the intersection by ≈1.44 years. Finiteness is unaffected.
Key Physical Facts
Landauer's Principle [1–3]
Erasing one bit requires ≥ kT ln 2 energy. Verified experimentally at classical and quantum scales. Implication: Deletion is a fixed tax that scales poorly at civilization levels.
Bekenstein Bound [4]
Maximum bits in a region scale with the surface area of the container and are saturated by black holes. For reference Schwarzschild radius rₛ = 1 mm, N_max ≈ 1.74 × 10⁶⁴ bits.
These facts are non-negotiable constraints on any physical information-handling system.
Core Assumption: Why Growth Must Occur
The proof relies on one weak, nearly tautological principle rooted in the definition of progress:
P1: Minimal Progress. Any non-stagnant, non-regressing civilization has effective average information growth r > 1 over long timescales.
This follows from the anthropic context of the Fermi Paradox: we look for observable civilizations, which presupposes growth (r > 1). Stagnation (r = 1) or regression (r < 1) naturally leads to silence through resource decay, so rejecting P1 implies civilizations never grow enough to be observable, trivially resolving the paradox.
Why Informational Growth Leads to Black Holes
Progressing systems (P1) evolve toward exponential information growth to minimize erasure costs (Landauer's principle). Hitting the Bekenstein limit triggers a density crisis: To continue, the system must pack bits at maximal density, requiring mass-energy concentration. This dynamic leads to gravitational collapse into a black hole if engineered, or to stagnation if not (both outcomes are externally silent).
The "informational singularity" is a phase transition. Externally, there are no emissions or expansion. Internally, computation runs at maximal efficiency.
Why Civilizations Don’t Expand Across Space
Why no sharding or interstellar spread? Surface-tension physics explains why sharding is energetically prohibitive.
Informational droplet. Water droplets minimize surface area to reduce energy loss. Distributed information has an "informational surface": Communication channels dissipate energy per Landauer (transmitted bits copied/erased). Sharding into n nodes at distance d increases surface ~ n d, raising costs.
E_sharded ≥ E_central + n d kT ln 2 (for sync traffic). Non-zero d makes sharding strictly more expensive, favoring local centralization.

Figure 3 — Sharding increases “informational surface” and dissipation. Centralisation minimises it.
The Core Theorem: Finite-Time Singularity
From facts and principle follows the theorem: Any r > 1 reaches finite N_max in finite t (machine-proved in BlackHole.lean).
Proof intuition: On a log scale, exponential growth is an upward line while the bound is horizontal. Non-parallel lines intersect — a geometric inevitability.
Illustrative Calculation: Time to Singularity
For illustration under a minimal loss-free growth baseline (φ-rate), see the forecast table and figures above.
Sensitivity (Appendix B): All parameter variations shift timelines slightly but preserve the inevitability of finite-time collapse.
Implications
The theorem reframes the Fermi question. Rational optimisation drives civilisations inward rather than outward, so the expected observable state is a silent, highly-dense “computational black hole”. Sharding or interstellar spread remains theoretically possible, yet the energy overhead of synchronising distant shards (Fig. 3) makes expansion uneconomical, so collapse or stagnation occurs first. In this view the Great Filter is not a catastrophic event but a predictable phase transition that every progressing culture eventually crosses.
For humanity the illustrative φ-baseline places the transition approximately 192 years ahead, implying that data-retention economics (not spaceflight) will dominate the next two centuries. Observable consequences follow: we should not expect Dyson-scale engineering, but rather compact, low-emission systems. SETI efforts should thus prioritize searches for anomalous black-hole-like objects or unexpected infrared voids.
Recent JWST rotation asymmetry [6] aligns with the model’s focus on local optimisation. If the signal reflects cosmic rotation the centripetal trend only strengthens, if it is a Doppler calibration issue, timelines slightly rescale (Fig. 2) yet remain finite.
Counter-scenarios (for example, near-free data erasure or exceptionally efficient sharding) barely shift the timeline. True stagnation (r ≤ 1) avoids collapse, but such civilizations remain silent by definition.
Verification: Proofs, Code, Reproducibility
Mathematics verified in Lean4 (mathlib4; no 'sorry's/axioms):
- φ-Minimality (PhiMinimal.lean): r ≥ φ for lossless baselines.Time-to-Threshold (BlackHole.lean): Finite t for r>1.
lake build verifies.
Python (get_phi_years.py) reproduces tables/figures.
Repo: https://github.com/DanielSwift1992/veritas-black-hole-article
Note: N_max ∝ rₛ². Rescaling shifts timelines by Δt = ln(factor)/ln r. Finiteness is preserved.
Appendix A: Bekenstein Bound Example (1 mm Black Hole)
r_s = 10^{-3} m.
M = (r_s c^2)/(2G) ≈ 6.74 × 10^{23} kg.
A = 4π r_s^2 ≈ 1.2566 × 10^{-5} m².
S = (k_B A c^3)/(4 ħ G) ≈ 1.66 × 10^{41} J/K.
Bits = (S/k_B)/ln2 ≈ 1.74 × 10^{64}.
Appendix B: Sensitivity Analysis
Robustness: All parameter variations alter timelines by at most logarithmic factors, yet finite-time collapse remains unavoidable.
| Variation | Change | t (years) | Year |
|---|---|---|---|
| Larger BH (1 cm radius, N_max × 100) | N_max ×100 | 202 | 2227 |
| Partial deletion allowed (r = 1.50) | Growth rate ↓ | 228 | 2253 |
| Massive expansion (N_max × 10¹⁰) | N_max ×10^{10} | 240 | 2265 |
| Doppler recalibration (N_max × 2) | Distance scale ×2 | 194 | 2219 |
Generated by get_phi_years.py. Doubling N_max adds ln 2 / ln φ ≈ 1.4427 years (exact script output).
References
[1] R. Landauer, IBM J. Res. Dev. 5, 183 (1961).
[2] A. Bérut et al., Nature 483, 187 (2012).
[3] L. L. Yan et al., Phys. Rev. Lett. 120, 210601 (2018).
[4] J. D. Bekenstein, Phys. Rev. D 23, 287 (1981).
[5] J. M. Smart, Acta Astronaut. 78, 55 (2012).
[6] L. Shamir, Mon. Not. R. Astron. Soc. 538, 76 (2025); arXiv:2502.18781. [7] IDC, “Global DataSphere Forecast, 2023–2027” (IDC Doc # US50505223, 2023).
Discuss

