Simplex团队深入研究了AI系统的内部表示和行为，发现Transformer模型通过注意力机制将信念状态几何化，并揭示了数据生成过程的谱分解在其中扮演的关键角色。他们还探讨了上下文学习（ICL）的本质，认为其源于训练数据的非马尔可夫性和非遍历性，模型需要推断数据源。此外，研究表明神经网络在处理复杂数据时会自然发现后经典计算表示，类似于量子计算，这为理解神经网络的计算本质提供了新视角，并为AI的可解释性研究开辟了新方向。

✨ **Transformer的几何化信念状态：** 研究发现，Transformer模型在处理序列数据时，其内部激活会根据数据生成过程的信念状态形成特定的几何结构。这表明模型并非随机处理信息，而是以一种结构化的方式组织其内部表示，与数据生成过程的隐藏状态紧密相关。

💡 **注意力机制的谱分解作用：** Transformer的注意力机制被揭示为一种并行化的贝叶斯处理方式，它通过分解数据生成过程的谱（特征值/特征向量）来更新信念状态。这种机制允许模型在有限的计算资源下，高效地处理序列信息并构建几何表示。

🚀 **上下文学习（ICL）与数据结构：** 上下文学习被解释为模型在处理非马尔可夫和非遍历数据源时，需要同时推断隐藏状态和数据源的自然结果。当训练数据包含多种异质性源时，模型通过学习不同数据源的结构来提升在特定任务上的表现，这解释了为何预训练模型能通过提示进行多任务学习。

⚛️ **神经网络的后经典计算能力：** 研究表明，神经网络在处理需要复杂经典计算才能生成的数据时，能够自然地发现并利用后经典计算表示，例如类似于量子计算的表示。这意味着神经网络可能具备超越传统计算模型的潜力，能够以更有效的方式建模复杂数据。

Published on July 28, 2025 9:58 PM GMT

Thanks to Jasmina Urdshals, Xavier Poncini, and Justis Mills for comments. 

Introduction

At Simplex our mission is to develop a principled science of the representations and emergent behaviors of AI systems. Our initial work showed that transformers linearly represent belief state geometries in their residual streams. We think of that work as providing the first steps into an understanding of what fundamentally we are training AI systems to do, and what representations we are training them to have.

Since that time, we have used that framework to make progress in a number of directions, which we will present in the sections below. The projects ask, and provide answers to, the following questions:

How, mechanistically, do transformers use attention to geometrically arrange their activations according to the belief geometry?What is the nature of in-distribution in-context learning (ICL), and how does it relate to structure in the training data?What is the fundamental nature of computation in neural networks? What model of computation should we be thinking about when trying to make sense of these systems?

In answering these questions we find a number of surprising results, described in the rest of this post, and new ways of thinking about both specific parts of the transformer architecture, for instance what exactly the attention heads are doing, and more generally computation in neural networks overall that we believe have important implications for much of interpretability. We are currently expanding on these findings, both on the theoretical side as well as the applied side, pushing towards applications to LLMs at scale.

In addition to the work presented here, we've mentored fellows at MATS and PIBBSS, ran a hackathon with PIBBSS and Apart, that had a number of interesting results^[1], and are currently scaling up our team to build on these insights, with support and funding from the Astera Institute. We will finish by mentioning some directions we are exploring and excited to work on next.

For context, we will begin with a short summary of our foundational work. We will then give paragraph-length summaries of the answers to the 3 questions above, and then we will give longer summaries of each project. 

The foundational theory

In our original work, expanded on in our NeurIPS 2024 publication,  we developed a general theory connecting next-token prediction to the geometric structure of representations inside of trained transformers. Our key insight was that any system trained to predict the next token in sequences should maintain beliefs about the hidden states of the process generating those sequences. These belief states—probability distributions over unobserved hidden states—have specific geometric relationships that can be derived analytically.

Crucially, the predicted geometric structure is distinct from the training data itself, and the correspondence between these is often unintuitive. The predicted geometry is not given directly by the structure of the token sequences, and not even by the data generating process. It is instead related to the metadynamic of belief updating over that hidden generator. This metadynamic is, in general, a lot more complicated in its computational structure than the generator of training data. 

We tested this theory using sequences generated by simple Hidden Markov Models (HMMs)^[3], which produce simple strings of tokens. Yet our theory predicted that transformers trained on these token sequences would internally organize their activations into complex geometric patterns. For instance, with a simple 3-state HMM we call "Mess3,"^[4] the training data consists of sequences like "ABABCAB..." but our theory predicted that belief states would form an intricate fractal structure within a 2-simplex.

When we trained transformers on these raw sequences, we found their residual stream activations spontaneously organized into exactly these predicted geometries—complex fractals emerging from simple token prediction. This validated our theoretical framework: transformers discover they need to maintain probabilistic beliefs about hidden states, and these beliefs naturally crystallize into specific, mathematically-determined shapes that are far removed from the surface structure of the training sequences. With this work we now have a theoretical bridge from the statistical structure of training sequences to the geometric structure of learned representations—a framework for theoretically predicting what internal structures transformers will learn, and why, from a given training data distribution.

Answers to the Questions

Since that time, we have made progress in a number of directions, which we will present in the sections below. The projects ask, and provide answers to, the following questions:

1. How, mechanistically, do transformers use attention to geometrically arrange their activations according to the belief geometry?

We find that the attention mechanism parallelizes recurrent Bayesian processing by decomposing the belief updating according to the spectrum (eigenvalues/eigenvectors) of the data generating process. This allows us, in the toy model that produced the original fractal results, to make predictions about the embeddings, OV vectors, attention patterns, and residual stream activations before and after the MLP^[5], that we verify in experiment. You can read more in our ICML 2025 manuscript.

2. What is the nature of in-distribution in-context learning (ICL), and how does it relate to structure in the training data?

We show that ICL emerges from non-Markovianity and non-ergodicity of data sources. When training mixes multiple sources, models must infer, in addition to what hidden state the generating source is in, also which source is currently active. This hierarchical minimization of uncertainty necessarily leads to in-context loss decreasing as a power law with context length. Induction heads are a natural solution to this source disambiguation problem. You can read more on arXiv.

3. What is the fundamental nature of computation in neural networks? What model of computation should we be thinking about when trying to make sense of these systems?

Our initial work implied that activations in transformers should lie within a simplex^[6]. This seems like quite the restriction, given that the freedom of floating point numbers is available in the residual stream. We find that we can generalize our initial findings to a much broader computational class, that is more akin to quantum computation, and actually more general than that. In this more general computational class, belief states lie in more arbitrary convex sets. By training on toy stochastic processes that would require infinite-state classical computing systems to generate the training data, but a small finite set of post-classical states, we find that neural networks represent these post-classical beliefs, and not the classical ones. In other words, neural networks naturally discover quantum and post-quantum representations when these are the minimal way to model their training data. You can read more on arXiv.

Admittedly, these are quite technical answers (the last one is especially non-trivial to grok). In the sections below we outline, quickly, the intuition behind these results. Each is self-contained, so feel free to skip directly to whatever interests you. In the future we plan to make more thorough explainers for some of these projects, especially those that we believe have the most potential impact on mechanistic interpretability work.

Completed Projects

Constrained Belief Updates Explain Geometric Structures in Transformer Representations

Accepted to ICML 2025 (manuscript)

How, mechanistically, do transformers use attention to geometrically arrange their activations according to the belief geometry?

Taking our initial results seriously leads to a deep tension. Bayesian updating over a world model is fundamentally recurrent - you have an internal state, your belief, then you get new information from the world, then you update your belief, only to receive a new piece of information from the world, and then update your belief, and so on ad infinitum. This recurrent updating of internal states is at odds with the attention mechanism in transformers, which is very much parallel and not recurrent. So how is it possible that transformers are representing belief states?

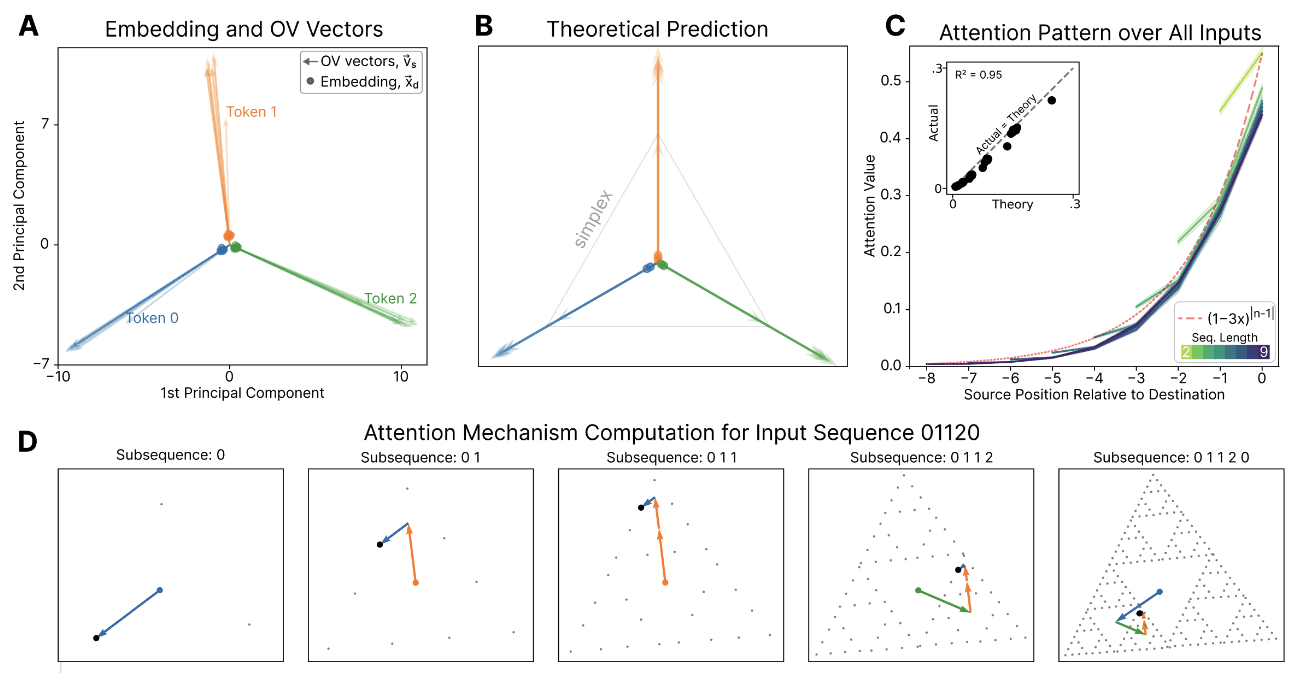
In this work we took the recurrent equations for belief updating and constrained them by the functional form of the attention mechanism in transformers, which only allows updates to a residual stream at a particular context window position to use information from previous context window positions in a restricted way. In particular, the OV-vectors which attention patterns weight in order to get the residual stream updates can only depend on information at the source position, and nothing else.

By constraining the model-agnostic belief updating equations with this constraint, we derive a constrained belief updating equation. Whereas the full belief updating equations answer the question “What is my belief over the hidden states of the generating process given the particular sequence of tokens I’ve seen,” the constrained belief updating equation is the answer to “What is my belief over the hidden states of the generating process given the particular sequence of tokens I’ve seen, if I’m only able to sum contributions that depend on looking back at particular sequence positions, and not the full sequence as a whole.”

This constrained form of belief updating has associated with it a constrained belief state geometry, which differs from the full (unconstrained) belief state geometry. Below are some examples of how the full belief state geometry compares to the constrained belief state geometry for 4 different parameter settings of the Mess3 process (this is the process from our original work that produces the fractal).

As you can see, the constrained belief geometries often differ quite a bit from the full ones. So what does this have to do with transformers? Well, we arrived at the constrained belief state geometry by constraining the information transfer from past histories to future predictions by the mathematical form of an attention head. Notably, in our original work we looked at residual stream activations after MLP sublayers. But if our theory is correct, the residual stream after the first attention layer, but before the first MLP, should look like these constrained belief geometries. Below you can see visualization (using PCA) of the activations after the first attention layer but before the MLP (we call these “intermediate” activations), as well as after the first MLP (we call these the “final” activations). We show both the predictions of our theory as well as the empirical results.

Just to reiterate, this is straight up PCA of the activations, so an unsupervised analysis of the geometry found in the residual stream. The theory of constrained belief updating works well for these intermediate activations (though not perfectly; we do have a few leads for these deviations).

In addition to the residual stream geometries, we are able to make predictions for the embedding, OV vectors, and attention patterns. To do this we notice that the constrained belief updating equations have terms in the form of a stochastic matrix to integer powers. The stochastic matrix is the one governing the dynamics of the hidden states of the data generating process. Matrices to integer powers have a natural decomposition in terms of powers of eigenvalues of that matrix. You will have to read the manuscript to follow all the math, but plugging in that decomposition allows one to express the constrained belief updating equation in a way that corresponds to the functional form of the attention update. By then putting terms in the two equations in correspondence, we can make predictions, which you can see in the figure below (B is the theoretical prediction for the embedding and OV vectors, with empirical results shown in A; C shows the attention patterns, with the insets comparing prediction to experimental results).

This additionally allows us to see that attention carries out an algorithm in the plane of the simplex, in order to build up the constrained belief geometry, which we can track and visualize, in D above.

We are excited about these results for a number of reasons:

This work connects the model-agnostic theory of belief state updating with the model-dependent focus of mechanistic interpretability. By doing so, we have an accounting of transformer representations as they relate to the hidden structure of the data generators they are trained on.This work provides a new conceptual and theoretical view of what attention is fundamentally doing - a spectral algorithm to compute Constrained Belief Updating. We developed a theoretical framework that analyzes how eigenvalues of the data-generating transition matrices determine attention heads’ behavior. By decomposing belief updates spectrally, we show that multi-head attention naturally implements these scalar updates in orthogonal modes through a sum of specialized head outputsThe theory we build up is both principled and empirically testable. We care very much that our work doesn't overly abstract away the normal operating mode of transformers, because in order for the theory to eventually do work in the real world, we need it to apply at scale. Our experiments, though in a toy setting, were able to make predictions for all activations in the small transformers we tested.

Next-Token Pretraining Implies In-Context Learning

(manuscript)

What is the nature of in-distribution in-context learning (ICL), and how does it relate to structure in the training data?

Before LLMs, it was largely the case that particular types of tasks, for instance sentiment analysis or answering multiple choice questions, would require optimizing different networks for each. By pretraining transformers on next-token prediction over a large text corpus, LLMs seemed to be imbued with a natural ability to be prompted, after training is completed and weights are frozen, on any of those tasks and to be better at those tasks compared to narrower, task specific systems. Where does this ability come from, and how does it relate to the training data structure?

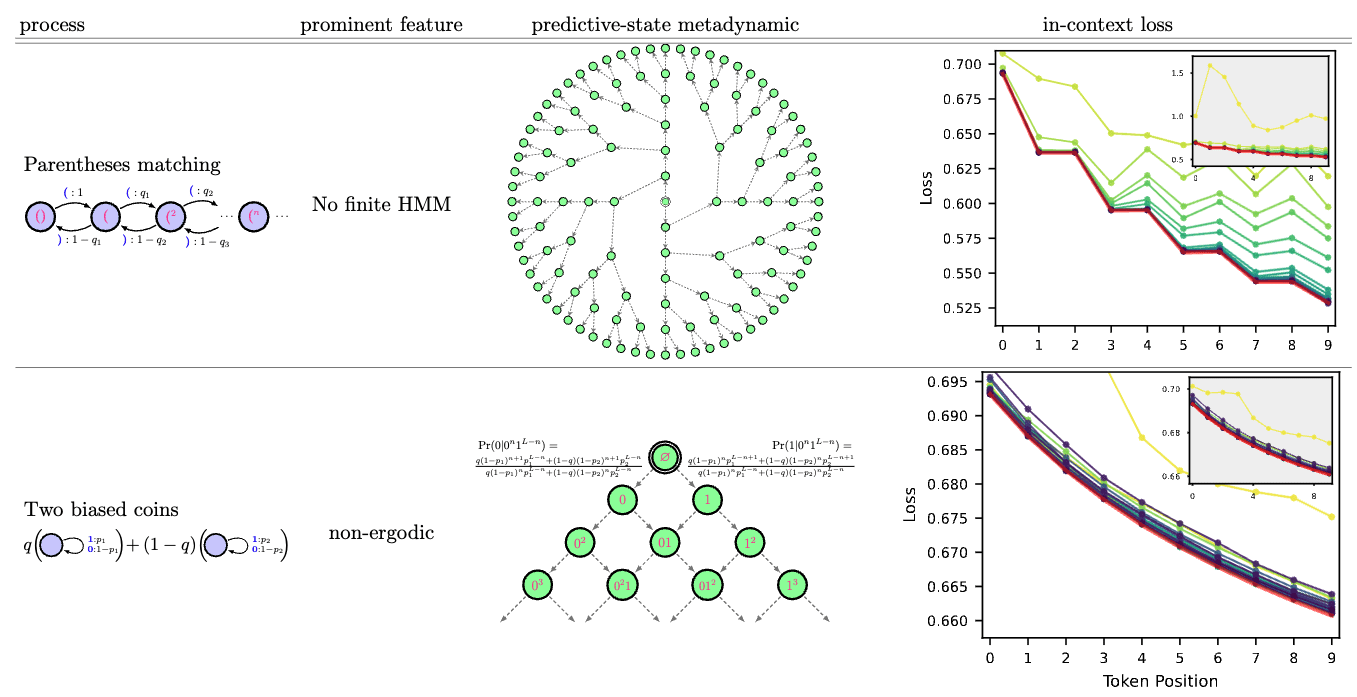
This work establishes the relationship between training data structure and in-context behavior. Belief updating over a world model gives a natural and formal answer to how loss should decrease as the tokens in a prompt decrease uncertainty over the states of the data generator. For a number of examples we show both the structure of the belief update (predictive-state metadynamic), as well as the implied in-context loss, which we show to be equal to something called the “myopic entropy” of the data generator. In experiments, we find that in-context loss converges to the myopic entropy.

Real training data will be non-ergodic, and this has important implications for in-context behavior. A non-ergodic data generator can be thought of as consisting of multiple independent sources. For instance, the data LLMs are trained on contains text samples from Reddit, Wikipedia, and Python code. Each of these sources of data have distinct correlational structures. The generation of data from this non-ergodic set is a two-step process. First, choose a source, and then have that source generate a string of tokens. To get the next sample one must first choose a source again, before generating tokens from that source.

Due to this non-ergodicity, belief updating has a hierarchical structure. Not only does a transformer need to infer what hidden state the source is in, but it also needs to infer what source is currently active. If one thinks of different types of tasks as different sources, then it becomes easy to see why prompting a pre-trained LLM with a few examples of a type of task helps it infer the task, and allows it to be better at the task. It is a natural consequence of belief updating over non-ergodic training data.

Similarly, one can think of the different sources as different personas. The vibe of the prompt you give an LLM will then elicit belief updating over the different personas and will direct its activations to parts of belief space that correspond to increasing certainty over the personas who create text with those types of vibes.

One can test the theory of belief updating over non-ergodic training data in toy settings. Even a non-ergodic source consisting of e.g. N=29 coins with biases towards heads evenly spaced between p=1/(N+1)=1/29 and p=N/(N+1)=29/30 gives interesting predictions about in-context behavior.

First, imagine you receive strings of heads (H) and tails (T) that you know are generated from one of the 29 coins mentioned above, but you don’t know which one. Unbeknownst to you, it happens to be the case that you receive a string of Hs and Ts generated from a fair coin (the fair coin is part of your training dataset, p=15/30). As you begin to see Hs and Ts, how should your loss on next-token prediction scale as you see more tokens?

First, you will either see an H or a T. If you see an H, then you update your beliefs over sources that are more likely to give Hs, and thus a lot of your beliefs will be over sources with biases towards heads. This will be true until you see enough tokens to override the spurious correlations and realize that the token sequence was most likely generated by a fair coin. Thus, early on in the token sequence you actually get worse on the task of predicting a random coin, and then only later decrease to the entropy (1 bit) of a fair coin toss. This transient increase in loss is worse, and your synchronization to the 1-bit fair coin is slower, the more coins you’ve been trained on, according to the theory, and also in our experiments. One major lesson of our work here is that the behavior of a transformer in context is not only dependent on the specific task that is in the context window, but depends more widely on the non-ergodic set of tasks and sources it was trained on.

Additionally, this toy setting predicts that non-ergodicity gives rise to power-law scaling of loss in context, which is indeed seen in LLMs. The power laws come from the hierarchical nature of Bayesian updating in the non-ergodic case^[7]. This doesn’t require enormously sophisticated training data, it just requires non-ergodic training data, as we see both from our theory and in our experiments.

Another interesting aspect of this story is that it conceptually connects to induction heads. Induction heads can be thought of as a natural solution to the source disambiguation that is a necessary part of belief updating over nonergodic data. We ran experiments where we trained transformers and RNNs over simple toy non-ergodic training data and found preliminary evidence for induction head formation, like phase transitions in the loss over training, similar to Anthropic’s findings on induction head formation. Interestingly, evidence for a phase transition occurred in both transformers and RNNs. Of course, RNNs can’t literally be creating induction heads, since they have no attention mechanism. Which begs the question, what are they doing exactly? This at least gives a hint that induction heads are actually a specific instance of a more general class of source disambiguation or generalization mechanisms.

We are excited about this work because it sets the stage for a principled understanding of out-of-distribution generalization. It is becoming clear to us that behavior and representations over the training dataset are largely determined by the training dataset itself, while out-of-distribution behavior will depend additionally on specifics of the architecture. Leveraging our understanding of in-distribution belief updating from this project—and the fact that all architectures pretrained on next-token prediction must find a way to implement these belief updates over the training data—we want to study how different architectures generalize out of distribution. Our Constrained Belief Updating results describe the transformer architecture dependence of representations. Explaining out of distribution generalization will require combining, and pushing beyond, these insights.

Neural networks leverage nominally quantum and post-quantum representations

What is the fundamental nature of computation in neural networks? What model of computation should we be thinking about when trying to make sense of these systems?

Methods in interpretability often rely on implicit, and sometimes explicit, assumptions about the nature of computation and representations in transformers. For instance, the structure of sparse autoencoders (SAEs) is motivated by the work on superposition in neural networks. In this framing, there is a sort of platonic neural network that has many neurons (many more than exist in an LLM for instance), and whose activations are sparse in response to inputs^[8]. In the platonic network, these sparsely activated “features” are orthogonal. Actual neural networks don’t have enough neurons to implement this platonic network directly. Instead, they must cram these orthogonal, sparsely activated, features into their relatively small set of neurons. They can do this by using an overcomplete basis, under the assumption that the basis elements are sparsely activated.

This line of thinking, about the structure of the platonic network and how an actual neural network will try to implement it, justifies the structure of an SAE — an autoencoder with a large number of latent states, with a sparsity term^[9] added to the loss, that is trained to reconstruct the activations. The SAE is designed to reverse the cramming of the platonic network into the actual network, and to reconstruct the activations in the platonic network.

But what actually is the nature of such a platonic network, and its activations in response to inputs? If we had a more fundamental understanding of this issue, perhaps we could redesign SAEs to more faithfully decompose LLM activations into the feature set that is more true, in the sense that these internal representations would more accurately capture the computational set of elements the LLM uses to compute, not according to how humans might expect them to, but according to how they do. We think of these as features, representations, and computations defined on the network's own terms.

Our original work hinted at an answer to this question for networks trained on next-token prediction. Fundamentally, networks trained on next-token prediction are trying to represent belief states over the hidden structure of the data-generating process which generates the training data. This is true because these belief states, and the input-driven dynamics amongst them, really is the computational structure of next-token prediction. This is at least the beginning of an answer as to the nature of the platonic network.

Because beliefs are distributions over the necessarily mutually exclusive hidden states of the generating process of our training data, our initial work implied that activations in transformers should lie within a simplex. Indeed, even in the small toy examples used in our work, multi-dimensional, highly non-orthogonal, intricately structured geometries emerge, that all live in a triangle. We see no reason why this type of geometric non-orthogonal structure shouldn’t be a major part of the story of computation in LLMs at scale.

However, given that the freedom of floating point numbers is available in the residual stream, having activations restricted to be within a simplex seems like quite the restriction. Where exactly does this restriction arise from in our framework, and how far can we relax things in order to get to a more natural understanding of computation in neural networks?

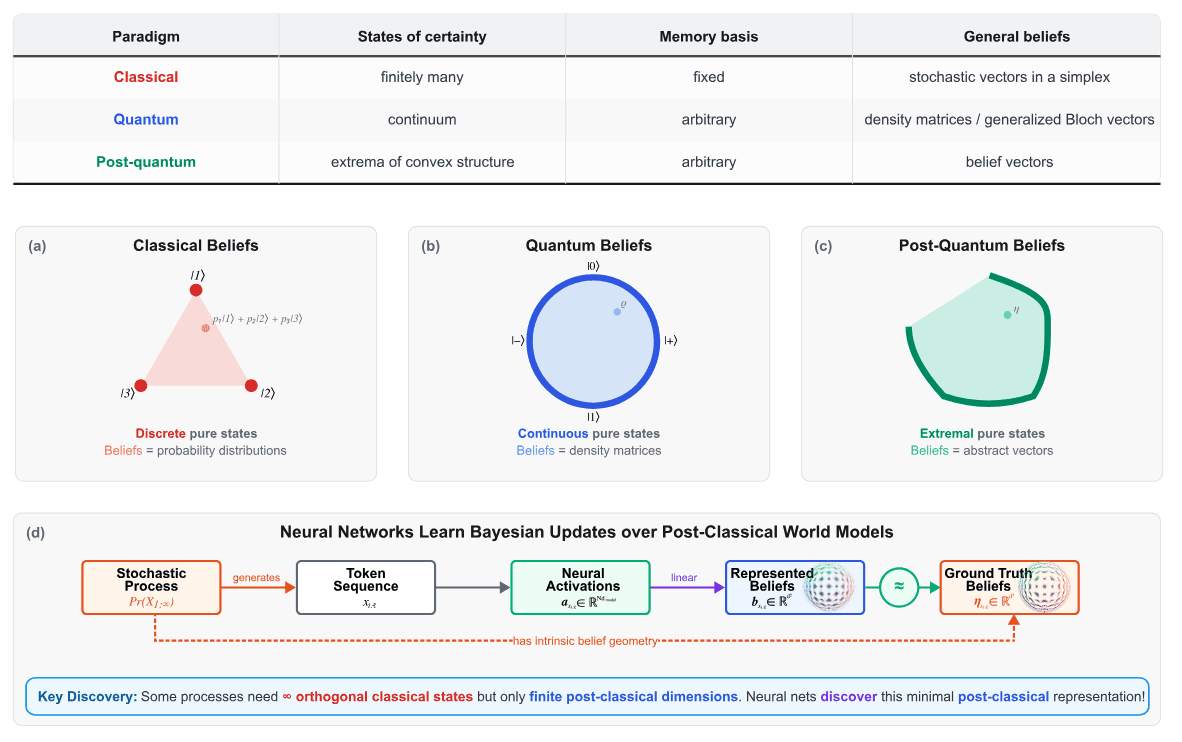
Note that the hidden states in a hidden Markov model (HMM) are mutually exclusive. If a system is in hidden state A, it is necessarily not even a little bit in any other hidden state. Thus, when our belief conveys 100% certainty that the HMM is in state A, this is orthogonal to the belief state of 100% certainty in state B. The motto here is that beliefs of total certainty (i.e., zero entropy) are orthogonal to each other.  All the states of uncertainty (i.e., entropy > zero), fill in the convex hull of those states of certainty, and that's where our simplex comes from.

We can relax this formalism quite a bit, in order to arrive at a much more general notion of computation that is the answer to the question “What is the most general notion of computation where we assume some minimal linear structure”? In particular, by allowing the beliefs of total certainty to be non-orthogonal and lie in a continuum, we arrive at a computational framework that has both classical and quantum computation as special cases, but also encompasses more exotic computational devices that don’t correspond to any currently known physics. In this more general class, belief states are harder to interpret, since they aren’t constrained to be probability distributions in the normal sense. However, they play the same computational role as in the HMM story, just in a more abstract way.

One can ask the question “how many states would be required for a classical computing device to generate this training dataset,” and for many processes that number would grow exponentially fast with sequence length, and in general could be infinite. Thus, to do next-token prediction well would require infinite-dimensional simplices, and often the belief states would be mostly orthogonal to each other. That same dataset, if generated by the more general class of computational devices, can often require only a small finite number of dimensions—for instance a few dimensions to represent a single qubit or small number of post-quantum bits. If transformers can represent beliefs over post-classical world models, then they can save large amounts of space in their residual streams.

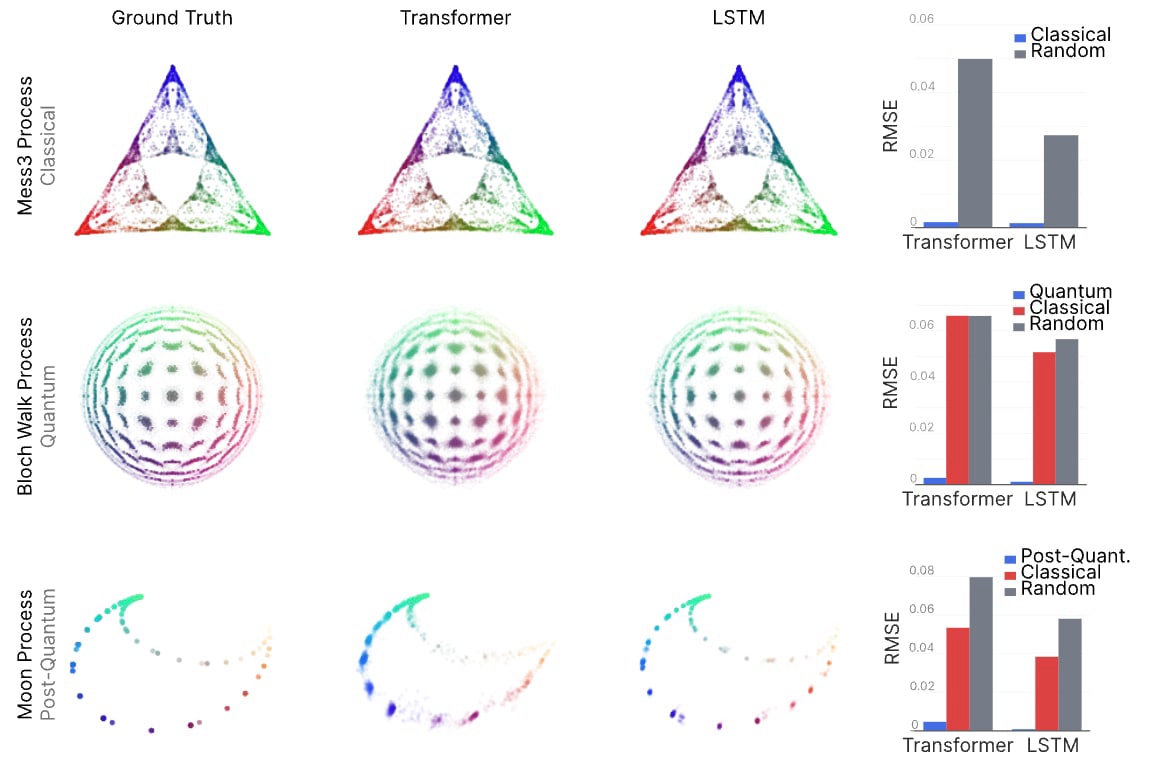
As examples, here are the belief geometries for three synthetic datasets, each having minimal data generators that live in different computational classes.

The first is the Mess3 process, which was our main example in our original Belief State Geometry work. This process has a minimal data generator which is an HMM (HMM’s are equivalent to finite classical computing systems) with three hidden states, and the belief geometry is a fractal in a 2-simplex.

The second we call the Bloch Walk Process, and would require infinitely many HMM states to generate, but only a single qubit for a quantum generator to make. All of its belief states live in a 2D slice of the Bloch sphere.

The third we call the Moon Process, and would require infinite-state HMMs for a classical generator and infinitely many qubits for a quantum generator, but only a small finite dimensional post-quantum system to generate. The belief geometry lives in a more arbitrary convex space, and the beliefs form a shape that looks like a moon.

When we train transformers and RNNs on these synthetic datasets, we find that they learn belief geometries associated with Bayesian updating over world models in the class of the minimal finite generators of the training dataset.

As before, we can look at how these belief geometries develop over training.

We are excited about this work because this helps us think more clearly about the nature of computation in neural networks, in quite a general sense. This framing is quite different from the normal way of thinking of computation in mechanistic interpretability, and we hope to have it do a lot of work, even at scale. We mentioned connections to SAEs, and we definitely will work applying the insights here to that domain, but we also want to emphasize that this is a very general way of thinking of computation, and should apply to many different questions in interpretability.

Thinking forward, this should help us to:

 Interpret and perhaps replace SAEsFind (possibly factored) belief geometry in LLMsDetermine which aspects of intelligent systems are universal, and which are architecture dependent.  Success in this will avail new opportunities for building a shared understanding of what we're building and its implications, for steering the technology and, one can hope, for better communication and empathy among intelligent systems.

Another note, we recognize that post-quantum computational theories aren't part of most people's everyday toolkit, and we're still working on finding the best ways to communicate these ideas. We plan on releasing a more thorough explainer about his work, as we do think it's foundational, and is a new way of conceiving of computation in transformers, and could act as a catalyst for a new approach to interpretability research.

 

1. ^{^}

   The winning projects included work on an unsupervised method of belief geometry recovery, showing that the original results generalize to RNNs, handcrafting a transformer to solve the RRXOR task, and Investigating the Effect of Model Capacity Constraints on Belief State Representations. We were surprised at the quality of the work that came out of this hackathon, so do check out all of the submissions if you are interested!

2. ^{^}

    

3. ^{^}

   Importantly, we train on the emitted tokens from the HMM, and not the hidden states or the beliefs themselves. This is important because the theory we develop is quite general to the normal setting of transformer pretraining. We train transformers to do next token prediction on datasets consisting of sequences of tokens, and our theory predicts what the geometry of activations inside the transformer should be.

4. ^{^}

   The strings of tokens, even in this simple toy HMM, have infinite Markov-order, meaning that there is correlational structure extending out backwards to the infinite past. In other words, the sequences of tokens are not Markovian. Tokens depend on information arbitrarily earlier in the sequence.

5. ^{^}

   Multi-Layer Perceptron - the feedforward network component that follows each attention layer in a transformer block.

6. ^{^}

   The restriction to simplices arises from the nature of the hidden states in HMMs. They are discrete and mutually exclusive in the sense that if you know with 100% certainty that the HMM is in a particular hidden state then you also know that it is necessarily not in any of the other hidden states. This corresponds to the nature of memory states in classical computing paradigms, where memory states are mutually exclusive (if the state of your classical bit is 0, then it is necessarily not in state 1). Thus, the vertices of a simplex correspond to distinct memory states in the paradigm of classical computation.

7. ^{^}

   It's known that power-law scaling of in-context loss can also arise from a single ergodic component with context-free or more sophisticated grammatical structure.  We don't yet know how these two sources of power-law decay of uncertainty play off of each other.

8. ^{^}

   This Platonic neural network is supposedly a reflection of the Platonic structure of the data itself.

9. ^{^}

   Originally, but not always these days, an ${\ell }^1$ penalty.

10. ^{^}

     

11. ^{^}

    Since the original post it's been accepted to Neurips. The manuscript there has more analysis than the LW post.

Discuss