DRUGAI
多保真贝叶斯优化(MFBO)是一种加速材料和分子发现的有前景框架,因为不同精度的信息源可供使用,且成本各不相同。尽管在化学任务中具有潜在应用,但目前缺乏对影响 MFBO 的诸多参数的系统评估。研究人员在此提出了一系列指南和建议,用于决定在实验环境中何时使用 MFBO。研究人员探讨了 MFBO 方法在分子和材料问题上的应用。首先,研究人员在两个合成问题中测试了两类不同的采集函数,并研究了近似函数信息量和成本的影响。随后,研究人员利用这些实现和指南在三个真实发现问题上进行了基准测试,并与其单保真对应方法进行比较。结果有助于指导未来将 MFBO 作为化学科学常规工具的应用。

众多机器学习技术中,贝叶斯优化(BO)已成为化学领域实验设计的首选方案。BO 基于概率模型,由两部分组成:一是用于近似实验过程的概率模型,二是决定数据采集策略的策略函数。比如,研究人员在寻求最大化某反应产率时,可利用模型预测下一步应测试的实验条件,以获得理想结果。该方法已成功应用于化学反应、功能分子或纳米晶体形貌等优化任务中。通过迭代学习循环,研究人员能够在广阔的搜索空间中快速找到最优条件。
传统 BO 已在实验领域得到广泛使用,但若研究人员能够以更低成本获取不同可靠性的数据,将进一步提升实验设计效率。某些可获得的低精度实验数据(如台式核磁数据)可以与昂贵的高精度实验结合使用。在实验设计中,引入不同可靠性的数据源称为多保真贝叶斯优化(MFBO)。此时,每种信息源(即保真度)都会被分配特定成本。多保真概率模型能够利用不同保真度的数据学习目标过程,并理解其相互关系。采集策略则需同时考虑查询某一保真度的总体成本。通过结合便宜但近似的低保真(LF)数据与昂贵且精准的高保真(HF)数据,总体优化成本相比单保真 BO(SFBO)可显著降低。
尽管 MFBO 在过去十年间在机器学习社区引起关注,催生了多种模型与采集策略,但实验研究人员仅在最近才开始将其纳入设计流程。在化学领域,也逐渐出现了在 BO 循环中引入成本意识的研究。然而,目前对于 MFBO 性能评估缺乏统一标准,不同研究工作对其性能的呈现方式差异较大。这种缺乏一致性的方法学阻碍了 MFBO 在实验界的广泛应用。
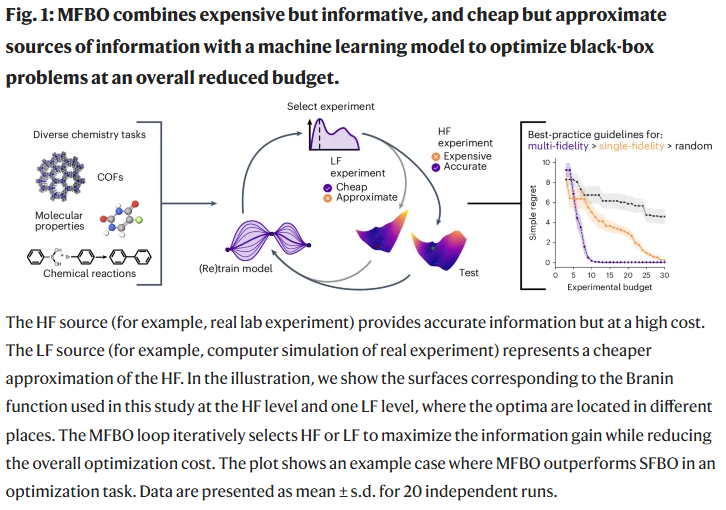
为此,研究人员提出了使用 MFBO 的指导准则。通过对合成黑箱问题和基于化学的任务进行详尽实验,研究人员明确了何时 MFBO 优于 SFBO,并为未来在分子与材料发现中的应用提供了参考。
结果
MFBO 失效模式分析
研究人员在两类采集函数(期望改进 EI 和最大熵搜索 MES)下,比较了 MFBO 与 SFBO 的性能。通过 Branin 和 Park 两个合成函数,研究人员验证了 MFBO 在信息丰富且低成本的 LF 源下能更快收敛并减少资源消耗。然而,当 LF 数据成本上升且信息度下降时,MFBO 的优势明显减弱,甚至不如 SFBO。
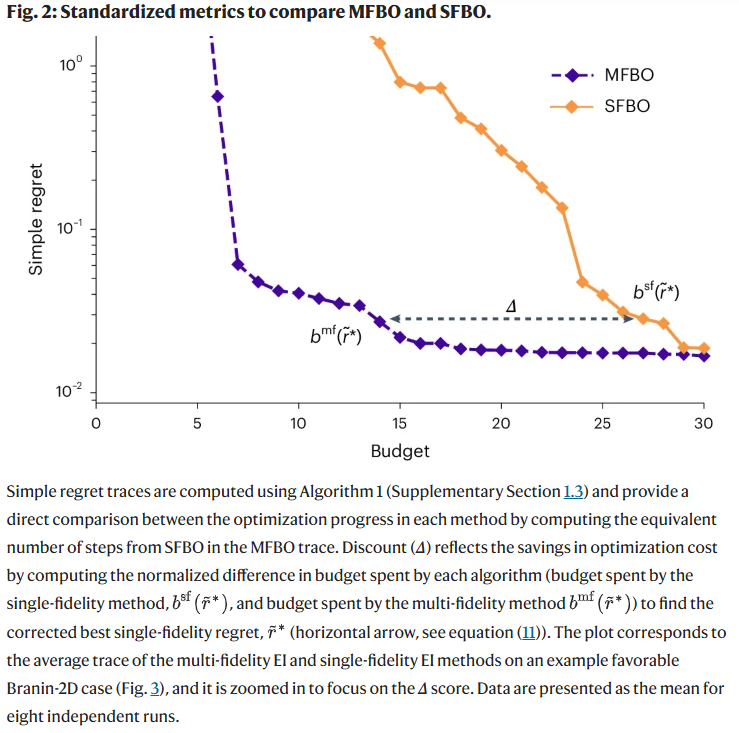
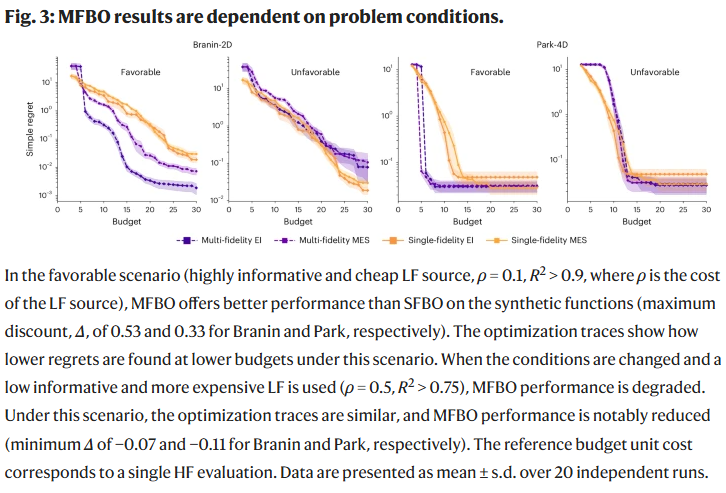
确定适用 MFBO 的条件
研究人员深入研究了 LF 数据成本和信息度对 MFBO 性能的影响。实验表明,只有在 LF 源既便宜又具有高相关性(R² 较高)时,MFBO 才表现出正折扣(Δ>0),即成本节省优势。若 LF 源成本过高或与 HF 源相关性差,MFBO 可能适得其反。
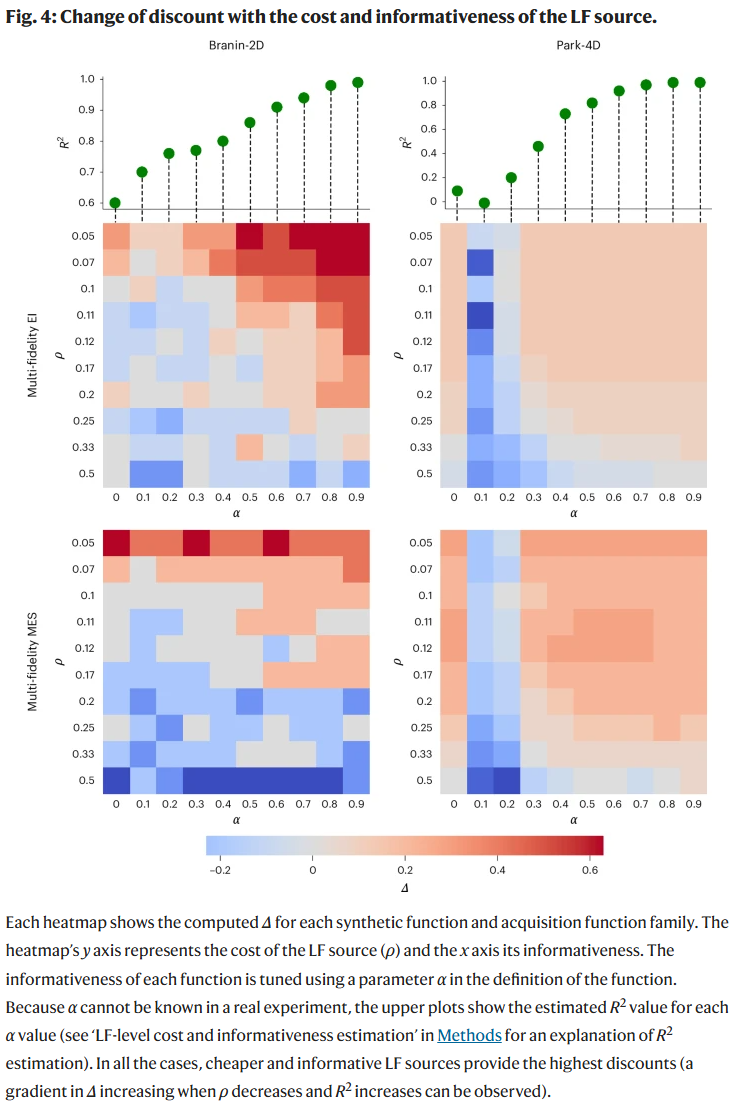
MFBO 在化学与材料问题中的应用
研究人员在三个实际基准任务上评估了 MFBO,包括共价有机框架(COFs)、溶剂化能和分子极化率。在这些任务中,MFBO 均优于 SFBO,能以更低成本获得更佳优化结果。例如,在 COFs 基准中,MFBO 提前收敛至低遗憾值,最大折扣 Δ 达到 0.68。然而,当将其中一个任务的 LF 条件人为调至不利场景时,MFBO 的性能被完全削弱,表明 LF 源的适用性至关重要。

MFBO 应用指南
研究人员提出了一份决策流程图,强调 LF 源的成本比(ρ)和信息度(R²)是关键指标。一般建议 ρ 0.8 才考虑 MFBO,以确保 LF 数据对 HF 数据具有足够参考价值。
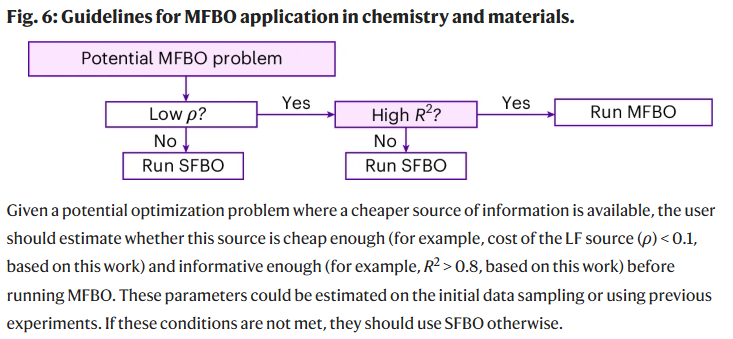
讨论
MFBO 通过引入廉价近似信息源,在优化任务中显著降低成本,尤其适用于化学科学领域。然而,其适用性并非普遍有效,若条件不佳,MFBO 可能不如传统 SFBO。研究人员通过综合分析明确了 MFBO 的适用条件,并提出了参数阈值(如最佳 LF/HF 查询比例约为 4:1)和 LF 源选择准则。
该研究的局限在于所有基准均为二元保真源,但近期研究显示多源 MFBO 也可成功应用于药物发现等领域。因此,未来工作将扩展至多保真多级信息源,并进一步研究模型不确定性校准、不同代理模型(如贝叶斯神经网络)以及特征空间的影响。研究人员的工作为在实验流程中引入 MFBO 提供了可行框架,有助于推动其在化学和材料优化中的常规应用。
整理 | WJM
参考资料
Sabanza-Gil, V., Barbano, R., Pacheco Gutiérrez, D. et al. Best practices for multi-fidelity Bayesian optimization in materials and molecular research. Nat Comput Sci 5, 572–581 (2025).
https://doi.org/10.1038/s43588-025-00822-9
内容中包含的图片若涉及版权问题,请及时与我们联系删除

