ICML'25 | 扩散模型的快速采样：可微分求解器搜索

本文分享阿里妈妈智能创作与AI应用团队在扩散生成模型上提出的快速采样方法。借助精心设计的可微分求解器搜索方法，可获取不同模型在给定步数下的高质量采样路径。基于该项工作总结的论文已被 ICML 会议录用，欢迎阅读交流。

论文：Differentiable Solver Search for Fast Diffusion Sampling

作者：Shuai Wang, Zexian Li, Qipeng zhang, Tianhui Song, Xubin Li, Tiezheng Ge, Bo Zheng, Limin Wang

论文地址：https://arxiv.org/abs/2505.21114

🏷 论文速读

本文提出了一个扩散模型求解器（solver）的搜索算法：给定模型和预期推理步数，可以高效地搜索出效果优秀的采样路径。

当前先进的采样器多基于线性多步法，通过仅与时间 t 相关的拉格朗日插值函数来提高少步数下的采样精度；然而对于给定扩散模型，仅与时间 t 相关的拉格朗日插值函数并不是最优解。本文通过数学推导，得出如下结论：插值函数具体形式并不重要，都可以通过预积分变成求解器系数，最终的采样误差仅由采样时间步和求解器系数决定。基于此，本文提出了一个非常紧致的搜索空间（仅几十个参数），即对效果最优的采样时间步和求解器系数进行搜索。

通过在 Rectified-Flow 模型、DDPM/VP 模型和多种文生图模型上的详尽实验，我们验证了上述方法的有效性和效果优越性。

1. 背景

图像生成是计算机视觉领域的一项基础任务，其目标是学习并捕捉原始图像数据集的内在数据分布，然后基于该分布采样以生成高质量的合成图像。近年来，扩散模型（Diffusion models）[1, 2, 3] 作为一种极具潜力的新方法，在一众图像生成方法中脱颖而出，性能显著超越了传统的生成对抗网络（GANs）[4, 5] 和自回归模型（Auto-Regressive models）[6]。

然而，扩散模型在推理时需要大量的去噪步，既带来了巨大的计算开销，也限制了其广泛应用。为了实现扩散模型的快速采样，现有的研究主要有以下两条技术路线：

1）基于训练（Training-based）的方法：通过步数蒸馏等技术，将快速采样的路径信息直接固化到模型参数中，从而跳过一些冗余的时间步。具体地，[7] 通过对齐“学生模型”单步生成的输出与“教师模型”多步生成的输出来减少推理步数，[8] 提出了“一致性模型”（Consistency Model），约束模型在任意时间步都能产出一致的预测结果。在此基础上，[9, 10] 进一步优化了训练过程中的离散误差，[11, 12] 利用了对抗性训练和分布匹配等技巧来提升生成样本的质量。然而，基于训练的方法存在一个最大的劣势：需要训练来微调模型参数，无法充分发挥出预训练模型的全部潜力。

2）基于求解器（Solver-based）的方法：通过逆向扩散过程的常微分方程（ODE）、人工设计求解器来实现更快的采样。例如，[13] 等工作指出了扩散ODE具有“半线性结构”，并据此提出了“指数积分器”来加速采样。[14] 则通过引入“预测-校正”结构进一步提升了采样质量。与基于训练的加速方法相比，基于求解器的方法有一个显著优势：它不需要调整模型参数，因此能够完整保留预训练模型的原始性能。此外，这类求解器可以无缝地应用于任何使用相似噪声调度器训练的扩散模型，具有很高的灵活性和通用性。正是基于这个特性，我们得以从扩散求解器的视角，去深入探索预训练扩散模型在极少步数下的性能极限。

目前，最先进的扩散求解器（如 DPM-Solver++ [13], UniPC [14] ）普遍采用类似Adams的多步方法，它们通过拉格朗日插值函数（Lagrange interpolation function）来最小化积分误差。但我们认为，一个优秀的求解器应当是为特定预训练模型量身定制的，所以我们提出了一种全新的、数据驱动的求解方法，在不破坏预训练模型的基础上实现快速采样。具体地，通过预积分方法（pre-integral）将插值函数简化为一组系数，我们可以在由“时间步”和“求解器系数”构成的搜索空间中进行可微分的求解器搜索，从而自动地找到最优的参数组合。

在上述方法的基础上，我们探索了预训练扩散模型在有限步数下的性能上限。实验表明，我们搜索到的求解器极大地提升了预训练模型的性能，并且遥遥领先于传统的求解器。在 ImageNet-256x256 数据集上，仅用10步，我们的求解器就使 SiT-XL/2 和 FlowDCN-XL/2 这类校正流模型（Rectified-Flow model）达到了 2.40 和 2.35 的FID分数，在经典的DDPM/VP模型上，我们的求解器帮助 DiT-XL/2 模型在 10 步内达到了 2.33 的FID，大幅超越了 DPMSolver++ 和 UniPC 等现有方法。对于像 FLUX、SD3、PixArt-Σ 这类文生图模型，我们在 ImageNet 上搜索到的求解器，在相同的 CFG scale（Classifier-Free Guidance scale）下，也能够持续生成比传统求解器质量更高的图像，证明了本方法的良好泛化能力。

2. 任务定义

为了让接下来的内容更容易理解，我们以扩散模型家族中数学形式既简单又优雅的 Rectified-Flow 模型作为讨论对象。当然，我们提出的算法并不局限于 Rectified-Flow 模型，我们会在后续内容中探讨它在 DDPM/VP 等其他扩散模型上的应用。逆向扩散过程可以看作是一个连续的积分问题，它被划分成了多个预先定义好的时间区间，即。假设我们已经有了一个预训练好的、可由常微分方程（ODE）来描述的扩散模型，那么在时间点，基于在此时刻之前所有时间点（从到）的采样信息：图像状态、时间以及由模型预测出的速度场，我们就可以把时间点到的这一小步等价于求解下面这个积分方程：

我们致力于开发一个更优的求解器，它能够在有限的采样步数（NFE）下最小化积分误差并提升图像质量，同时无需对预训练模型进行任何参数调整：

3. 方法

当我们重新审视 UniPC、DEIS、DPM-Solver++ 这类常用的多步采样法时，我们可以发现 Adams-Bashforth 方法中使用的拉格朗日插值函数并非扩散模型的最优解。更进一步，插值函数的具体形式是无关紧要的，因为通过预积分（pre-integration）和期望估计（expectation estimation），它最终可以被简化为一组系数。在后续的论证和实验中，我们证明了时间步和这些系数可以共同且有效地构成我们的搜索空间。

3.1 重温多步法

如下公式所示，欧拉法（Euler method）使用作为整个积分区间上速度的估计值，而更高阶的多步求解器则通过引入插值函数和先前已采样的值来进一步提升积分的估计质量。

最经典的多步求解器是 Adams–Bashforth 法，它通过引入拉格朗日多项式来提高给定区间内的估计精度。

如上所示，拉格朗日多项式中的积分项可以被预先计算成一个常数系数，这样在求解 ODE 时就只需要进行简单的求和运算。当前最先进的多步求解器，如 DPM-Solver++ 和 UniPC，都深受 Adams–Bashforth 这类多步求解器的启发，利用插值函数或差分公式来估计给定区间内的值。

然而，拉格朗日插值函数以及其他类似方法只考虑了时间，而速度场的计算同时需要作为输入。通过对在处进行一阶泰勒展开，并对在处进行高阶展开，我们可以很方便地推导出估计值的误差上界。

3.2 插值函数？求解器系数！

与典型的常微分方程求解问题不同，在考虑带有预训练模型的逆向扩散ODE时，存在一个紧凑的搜索空间。我们定义一个通用的插值函数来衡量与先前采样点之间的距离，以确定用于的插值权重。

我们假设对于，通用插值函数的余项是有界的，其界为，其中是关于的阶无穷小，而是关于的阶无穷小。

但上述公式存在一个循环依赖问题：的值也依赖于。为了消除这种循环依赖，我们简单地使用在处的一阶泰勒展开来替代其原始形式：

既然已经由和确定，那可以对公式做如下转换：

与简单的拉格朗日插值不同，这里的是一个关于当前的函数，而不仅仅是一个常数标量。学习一个函数会导致泛化能力的丧失，这限制了它在扩散模型采样中的实际应用。

给定采样时间区间，并假设。那么，Adams-like 线性多步法的误差期望为。将替换为其期望是最优选择，其误差期望为。所以，我们选择用的期望来替代它本身，这样我们就能获得与扩散调度器相关的系数，同时保持模型的泛化能力。

最终，对于给定的时间区间，我们得到了如下所示的优化目标，其中。这个期望可以被看作是通过大量数据和梯度下降来优化的结果。

3.3 可微分求解器搜索

通过前文的讨论和分析，我们确定了和为我们的目标搜索项。为此，我们提出了一种可微分的、数据驱动的求解器搜索方法。

时间步参数化（Timestep Parametrization）

如算法1所示，我们使用一组无界的参数作为优化对象。考虑到积分区间是0到1，我们通过一个 Softmax 归一化函数将转换为时间间隔增量，从而保证它们的总和为1。我们可以通过来得到具体的时间步，同时，我们将初始化为1.0，以获得一个均匀的时间步分布。

系数参数化（Coefficients Parametrization）

结合上述参数定义易知，速度场产生恒定值时，有一个隐式约束。这一观察启发我们将系数矩阵的对角线值重新参数化为。我们将非对角线的初始化为零，以模仿欧拉求解器的行为。

单调对齐监督（Mono-alignment Supervision）

我们采用一个步数较多（例如步）的欧拉求解器生成的ODE轨迹作为参考，使用均方误差（MSE）损失来最小化目标轨迹（我们N步求解的结果）与参考轨迹之间的差距，还采用了 Huber 损失函数作为对最终生成图像的辅助监督。

整体的搜索逻辑如算法2所示。将上述方法扩展至 DDPM/VP 等框架的细节请详见原论文。

4. 实验

我们在开源扩散生成模型上做了大量的实验以验证我们所提出的“可微分求解器搜索框架”的有效性，具体地，我们使用以 DDPM 方式训练的 DiT-XL/2、以 Rectified-Flow 方式训练的 SiT-XL/2 和 FlowDCN-XL/2 模型。训练设置方面，我们使用 Lion 优化器，固定学习率为 0.01，且不使用权重衰减。我们在整个搜索过程中约采样了 50000 张图像，以 FlowDCN-B/2 模型为例，8 张 H20 搜索 50000 个样本仅需要半小时。

4.1 Rectified-Flow 模型

ImageNet 256x256

我们在 SiT-XL/2 和 FlowDCN-XL/2 模型上验证了搜索得到的可微分求解器的效果。如下图所示，在 SiT-XL/2 上，我们搜索的求解器达成了更优的 FID 效果，在 10 步内就达到了 2.40（ FID 越小越好）。在 FlowDCN-XL/2 上，我们搜索的求解器在 10 步内取得了 2.35 的 FID ，大幅领先于传统求解器。

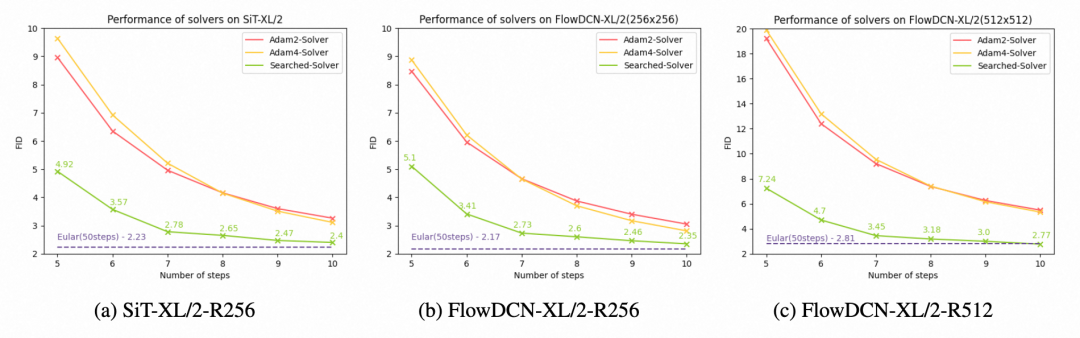
我们还与基于求解器的蒸馏方法（如 Flow-Turbo ）进行了比较，以展示我们所搜索求解器的效率。结果表明，在相似的函数求值次数（NFE）下，我们的求解器用更少的参数取得了更好的指标。

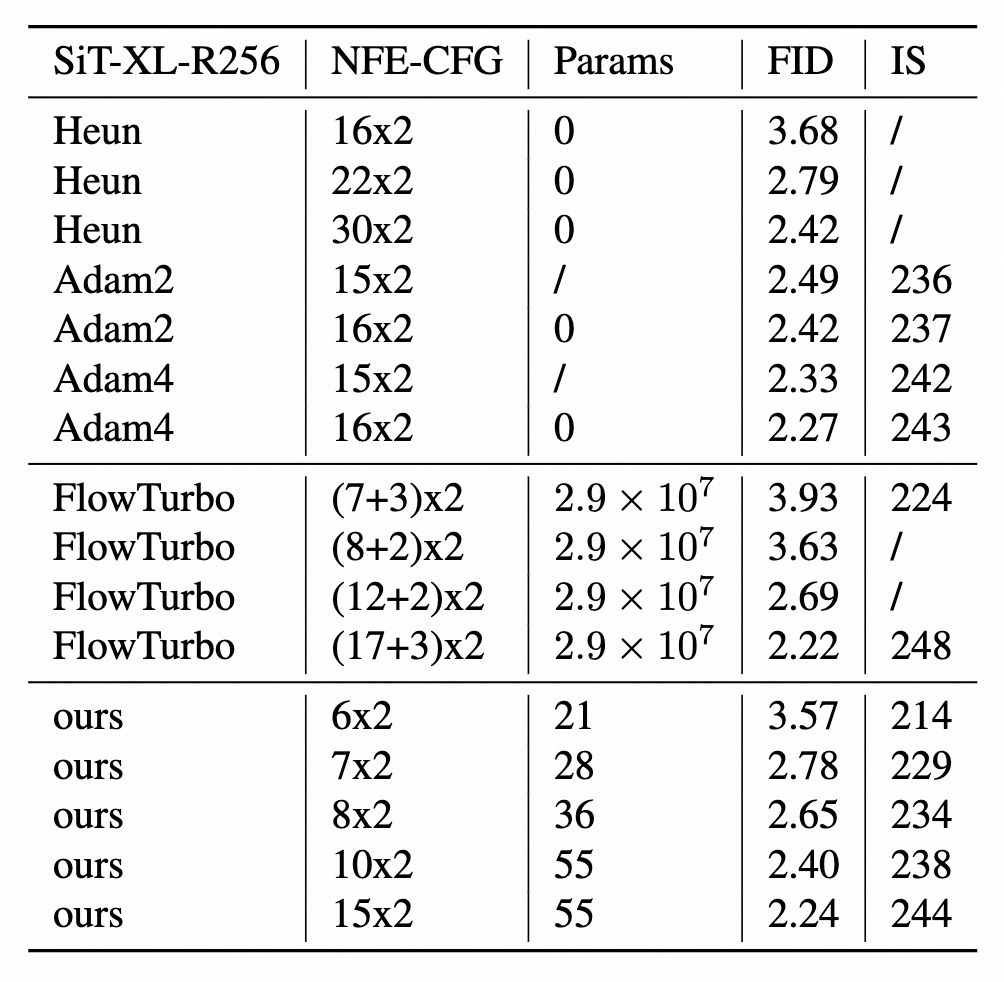
ImageNet 512x512

由于 SiT 的作者尚未发布在 512x512 分辨率上训练的 SiT-XL/2 模型，我们使用 FlowDCN-XL/2 的效果作为替代。我们搜索的求解器在 10 步内达到了 2.77 的 FID ，大幅领先于传统求解器，甚至略微超过了 50 步欧拉求解器的性能（FID 为 2.81）。

文生图效果

如下图所示，我们将基于 FlowDCN-B/2 和 SiT-XL/2 搜索到的求解器，应用于最先进的 Rectified-Flow 模型 Flux.1-dev 和 SD3，效果显著优于 Euler 采样器。

4.2 DDPM/VP 模型

我们选择在 ImageNet 256x256 上训练的开源 DiT-XL/2 模型作为搜索模型来进行实验。我们在 ImageNet 256x256 和 ImageNet 512x512 数据集上，将我们搜索到的求解器的性能与 DPM-Solver++ 和 UniPC 进行了比较。

ImageNet 256x256

参考其他论文的设定，我们设置 DiT-XL/2 的 CFG 为 1.5，且只将 CFG 应用于前三个通道。如下表所示，我们搜索的求解器显著提升了 FID 效果，在 10 步内达到了 2.33 的 FID 。

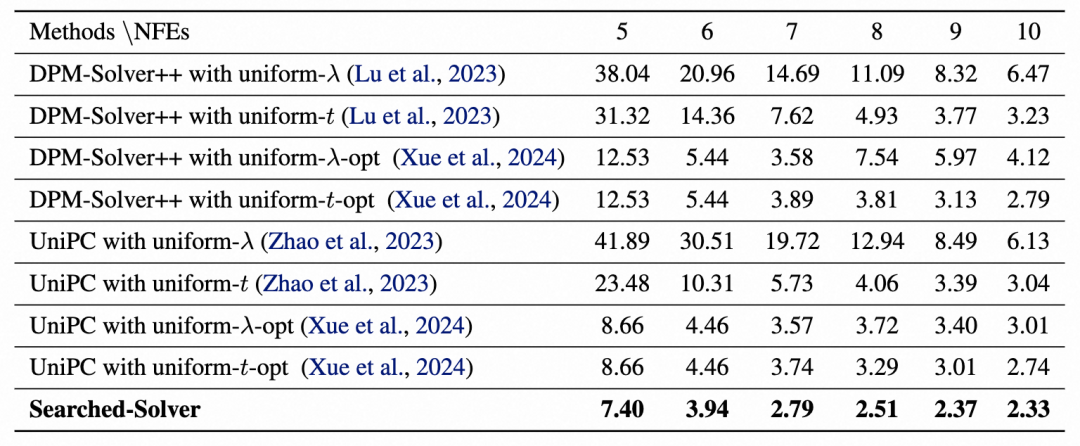
ImageNet 512x512

我们将在 256x256 分辨率上搜索到的求解器直接应用于 ImageNet 512x512 。结果也相当出色：DiT-XL/2 在 10 步内达到了 3.64 的 FID，大幅领先于 DPM-Solver++ 和 UniPC 。

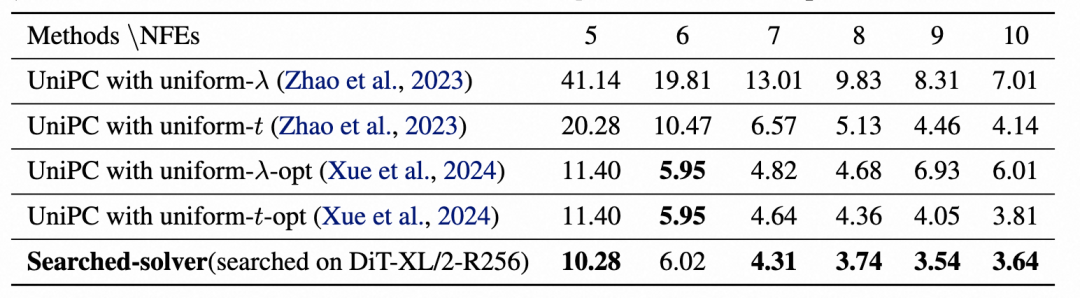
文生图效果

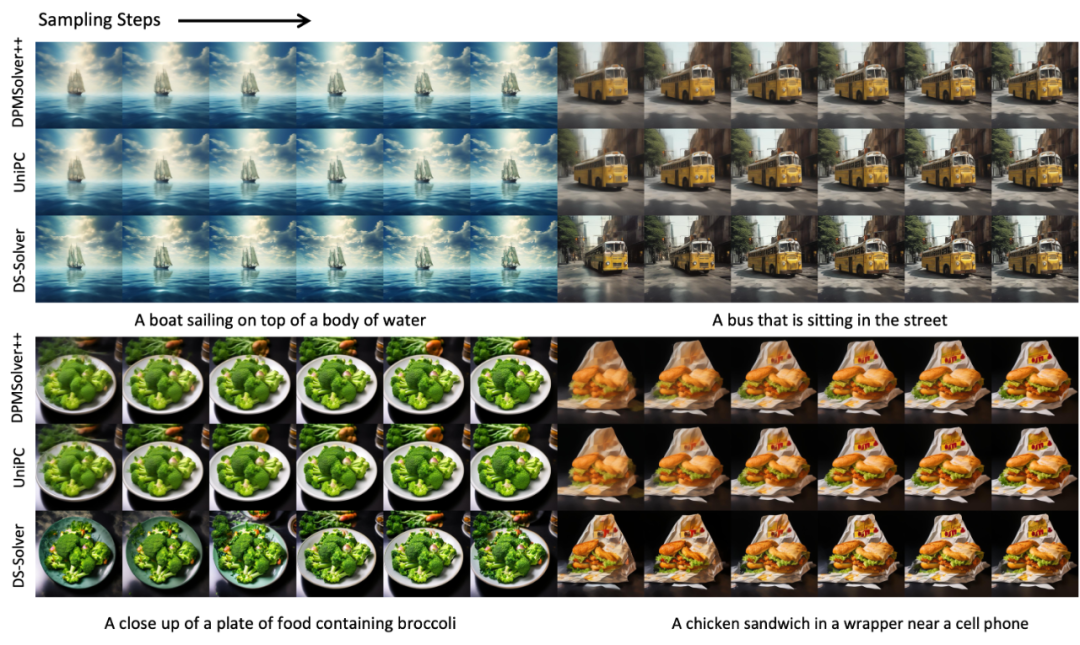
我们使用在 DiT-XL/2-R256 上搜索得到的求解器，在 CFG 为 2.0 的 PixArt-Σ 模型上进行推理。与 DPM-Solver++ 和 UniPC 相比，我们的结果始终展现出更高的清晰度和更丰富的细节。

4.3 求解器参数可视化

系数搜索结果（Searched Coefficients）

在下图左侧，我们对搜索得到的系数矩阵进行可视化：每个元素取值范围都是 0 到 1 ，越亮代表值越大。DDPM/VP 框架下，系数更集中于对角线，而 Rectified-Flow 框架下系数的分布更平滑。

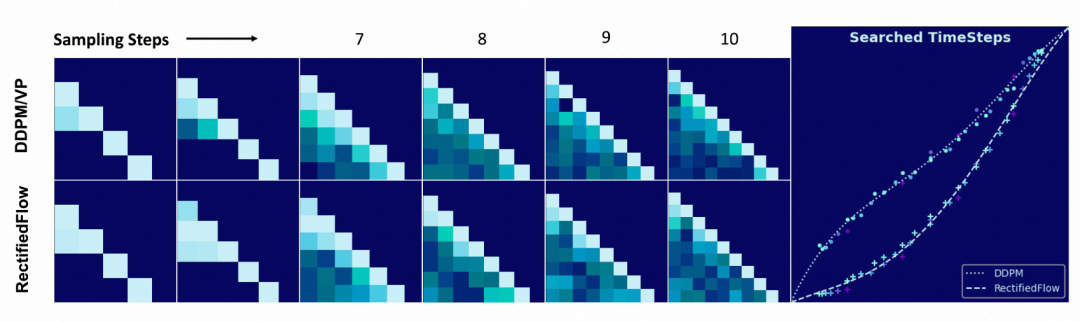
时间步搜索结果（Searched Timesteps）

如上图右侧，我们对时间步的搜索结果也进行了可视化。与 DDPM/VP 相比，Rectified-Flow 模型更关注噪声较多的区域，在初始阶段表现为较小的时间增量。我们用多项式对不同 NFE（函数求值次数）下搜索到的时间步进行拟合，可得到曲线拟合公式如下：

其中，并且表示噪声最强的时刻。

5. 总结

通过使用预积分技术将逆向扩散 ODE 的插值函数简化为一组系数，我们定义了一个紧凑的求解器搜索空间，同时提出了一种新颖的可微分求解器搜索算法来获取最优求解器。我们在 Rectified-Flow 框架和 DDPM/VP 框架下进行了验证，搭载了搜索的求解器后，模型的生成效果得到了显著提升。扩展到文生图扩散模型，利用 ImageNet 上搜索的求解器，我们能在相同的 CFG 尺度下生成较传统求解器质量更优的图像。考虑到 AIGC 时代日益膨胀的模型大小和飞速上涨的推理开销，本文提出的求解器搜索方法训练成本低廉，效果显著，有着巨大的落地价值和广阔的应用前景。

6. 参考文献

[1] Ho, J., Jain, A., and Abbeel, P. Denoising diffusion probabilistic models. Advances in neural information processing systems, 33:6840–6851, 2020.

[2] Song, Y., Sohl-Dickstein, J., Kingma, D. P., Kumar, A., Ermon, S., and Poole, B. Score-based generative modeling through stochastic differential equations. arXiv preprint arXiv:2011.13456, 2020b.

[3] Karras, T., Aittala, M., Aila, T., and Laine, S. Elucidating the design space of diffusion-based generative models. Advances in Neural Information Processing Systems, 35:26565–26577, 2022.

[4] Brock, A., Donahue, J., and Simonyan, K. Large scale gan training for high fidelity natural image synthesis. arXiv preprint arXiv:1809.11096, 2018.

[5] Sauer, A., Schwarz, K., and Geiger, A. Stylegan-xl: Scaling stylegan to large diverse datasets. In ACM SIGGRAPH 2022 conference proceedings, pp. 1–10, 2022.

[6] Chang, H., Zhang, H., Jiang, L., Liu, C., and Freeman, W. T. Maskgit: Masked generative image transformer. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, pp. 11315–11325, 2022.

[7] Salimans, T. and Ho, J. Progressive distillation for fast sampling of diffusion models. arXiv preprint arXiv:2202.00512, 2022.

[8] Song, Y., Dhariwal, P., Chen, M., and Sutskever, I. Consistency models. arXiv preprint arXiv:2303.01469, 2023.

[9] Zheng, J., Hu, M., Fan, Z., Wang, C., Ding, C., Tao, D., and Cham, T.-J. Trajectory consistency distillation. arXiv preprint arXiv:2402.19159, 2024.

[10] Song, T., Feng, W., Wang, S., Li, X., Ge, T., Zheng, B., and Wang, L. Dmm: Building a versatile image generation model via distillation-based model merging. arXiv preprint arXiv:2504.12364, 2025.

[11] Lin, S., Wang, A., and Yang, X. Sdxl-lightning: Progressive adversarial diffusion distillation. arXiv preprint arXiv:2402.13929, 2024.

[12] Zhou, M., Zheng, H., Wang, Z., Yin, M., and Huang, H. Score identity distillation: Exponentially fast distillation of pretrained diffusion models for one-step generation. In Forty-first International Conference on Machine Learning, 2024.

[13] Lu, C., Zhou, Y., Bao, F., Chen, J., Li, C., and Zhu, J. Dpmsolver++: Fast solver for guided sampling of diffusion probabilistic models, 2023.

[14] Zhao, W., Bai, L., Rao, Y., Zhou, J., and Lu, J. Unipc: A unified predictor-corrector framework for fast sampling of diffusion models. arXiv preprint arXiv:2302.04867, 2023.

END