Published on July 18, 2025 2:32 AM GMT
After 630,000 or so reviews with spaced repetition ("SR") and hundreds of hours of making and thinking about SR memory tools, here are some strong opinions held loosely:
1. Algorithm quality is overrated.
When people praise SR, it's (approximately) because SR minimizes the time and effort cost of learning a given fact indefinitely.
Now, what is that cost? For concreteness, let's say you want to be disposed to remember a given fact with probability at least p for the next five years. Doing that will require:
- The time it takes to research and make (or find and import, perhaps after modifying) the card, plusThe direct cost of doing a review (reading, answering, scoring) times the number of reviews it takes to maintain your memory, plusOther time and effort costs (switching decks, updating cards, modifying data-entry mistakes, working around bugs, and whatever else).
The promise of better SR algorithms is in lowering the number of reviews for the same amount of retention, but that is only one term in the equation above. Depending on who you are and what you're studying, it might require 10 reviews to maintain the memory you want for five years. A better SR algorithm might shave that down to 8 or 9. (This is on average: you can construct cases where an algorithm could save you more by, for example, saving you from starting over.)
For me, that's perhaps five seconds: my reviews take about three seconds each. And the differences between most SR algorithms won't even be that large.
Now, five seconds of savings times 50,000 flashcards (I'm a bit over that now) would be great. But that savings is more easily achieved by other means than algorithmic improvement. My own experiments in improving the UX of spaced repetition have saved more time than that, especially in improving the card-creation experience.
(A note on the arithmetic: If you're like me, you want to remember most of what you're remembering for much more than five years. Other SR users only worry about perhaps 6 to 48 months, and they have good reasons for that. Neither of these changes the calculation or basic conclusion much. For most use cases, there are larger and surer efficiency gains elsewhere than in improving the algorithm.)
2. We might know a lot less than we think we do about spaced repetition algorithms.
That's all true even if the conventional SR wisdom is perfect--that is, even if SR algorithms are optimizing for the right thing, and are in fact properly optimizing it. As grateful as I am for everyone who has contributed to SR research, I don't think we are.
My biggest fear about the quality of the research goes something like this:
- Cutting-edge SR research tends to be based on data generated by Anki.And that research tends to treat each card in isolation, at least in the sense that review times are calculated only in terms of a given card. (This assumption--that the review intervals for a card should depend only on a user's history with that card--is taken to be so obvious that it's usually not even mentioned.)But people often do--and, in my view, very much should--create many cards about related material at a given time.And, in a system that does not introduce random "jittering" or other mechanisms to spread out clumps of cards that come in together, that will cause the student often to have seen relevant material right before reviewing a given card.
A quick example:
- One day, the user makes or adds 10 cards about blood cells.The user immediately studies the cards, and gets 8 of them right easily.One day later, the user gets 7 of those 8 right again.Six days later--or however long their algorithm dictates--the user starts to study, and those 7 cards come back in a clump. They study the first 6, getting some right and some wrong.Now the user studies the seventh card. After their review, the algorithm will schedule the card again as if the material has only been seen three times: on days n, n+1, and n+7. But the user has, mere seconds ago, seen six cards' worth of related material.
Algorithms that consider only the history of a given card, therefore, are working with a huge blind spot. I suspect that addressing the blind spot matters much more for overall quality than algorithmic improvements do, in the current paradigm. (If you're fumbling around in the dark, a little bit of light will help you a lot more than better sneakers.)
I don't have a great algorithmic solution here, but I don't think I need one: It's not so hard to just make the problem go away. The clumping effect exists for two reasons: First, it's just how most SR software is designed; second, many users really want to adhere strictly to a deterministic algorithm. We can eliminate the first problem by designing our software differently, and we can eliminate the second problem by helping each other understand that adhering strictly to deterministic algorithms is not as good as it seems. (See below!)
Disclosure: I am at this point deeply invested in the idea that quite a lot of randomness ought to be involved in SR study. I've been living a less-clumpy SR life for years, now, and it feels great. I'm entirely sincere in everything I'm writing here, but at this point I'm motivated not only by these arguments but also because I like what I've built.
Maybe you're convinced that a lot more randomness in SR studying is a good thing, maybe not. Either way, I hope you're convinced that studying Anki data is studying data that's shaped in myraid ways by Anki's algorithm and the collective practices of the Anki community. Those effects, ignored by the algorithm, will matter a lot more than tiny improvements here and there to its coefficients.
This isn't just a theoretical worry. I now have a significant (>600k reviews) corpus of reviews done (mostly) with an anti-clumping system:
- It jitters scheduling intervals randomly, andIt inserts random cards from my corpus into my stream of cards to study. (Approximately 1/6 of my cards in any given study session are drawn randomly at random from the pool of not-due cards.)
When I try to train an FSRS-like model on these data, I can't get anywhere close to the ones other people are getting (Domenic Denicola has the best writeup I've seen about this).
Please take this only for what it's worth, because:
- I only record whether a response is correct or incorrect, not its difficulty on the standard SR 5-point scale, so I had to make some assumptions to apply the FSRS paradigm to my corpus;I've been as careful as I can be in trying to train a FSRS-like scheduler, but I am not an expert in this area;I am only one person, and perhaps I am unique in how I write cards and learn them.
If you want more details about my research here, or if you want to look at my data for yourself, please feel free to write to me. For now, please know that I've put in the work to generate less-clumpy data honestly; I've tried to train algorithms on that data; and the results seem to be way different from what you get by training on Anki data.
(For a small look at the data, please see the graphs below.)
3. ...and we might not be optimizing for the right thing, anyhow.
The goal of SR algorithms is, as standardly explained, to "make you study something just before you forget it." Since the best we can do is guess when you're about to forget something, this gets refined to: "make you study something just before the probability you would remember it drops below p, for some p you choose." This, in turn, leads SR researchers to frame algorithm development in terms of estimating p.
I suspect that the quality of our estimate of p is not the right thing to be optimizing. Earlier, I framed the central problem of SR as minimizing the total effort to maintain an acceptable level of recall for some given duration of time (possibly one's whole life). It is far from obvious that the best way to do this is to try to "study again just before you forget."
If we improved our estimate not of p but of how fast p is changing, we could focus our studying effort on the cards that are currently being forgotten most rapidly. (If your job was to minimize the water leaking through many holes in many dams, would you rather know, for every hole, how much water had already leaked, or the current flow? I'd much rather know the latter.)
Studying the rate of change of p over time would also help us understand how to optimize early reviews and late reviews. Human beings leading human lives can't stop what they're doing to study each card at the optimal moment: if someone has ten minutes they want to use studying but are "caught up," how can we best help them use that time? It is far from clear that "next due" is the most efficient set of cards to offer them. Again, knowing something about the rate of change of p would be useful here.
Maybe we don't have a good way to estimate the rate of change of p, and maybe there are good arguments that p itself is a good proxy for the slope of p (or some other quantity of interest). Even so, there are other potential benefits to thinking in terms of the expected value of the total effort required to retain a given fact.
Suppose we're deciding whether to study a fact now or later. If both the hypothetical current and future reviews have the same result, we benefit: the later review did not cost us retention, and we save some number of reviews over the long run. If the hypothetical future review is incorrect and the hypothetical current review is correct, we pay a cost: the expected cost to relearn and retain the fact between the later review and the end of the time window we care about goes (usually) way up.
We might then make this scheduling decision (now or later?) by trying to estimate:
- The probability we forget the fact between now and later;The expected value of the number of reviews saved in the "waiting is good" case;The expected value of the number of extra reviews required in the "waiting is bad" case.
Again, we might need to expand our view beyond estimating p in order to make this sort of decision properly.
4. So what should we do about this?
If I'm right about the above:
- The practical difference between good-enough algorithms is small compared to efficiencies you can get elsewhere in your SR practice;We might be systematically and significantly deceived about which algorithms are better and worse;Those algorithms might be optimizing for the wrong thing in the first place.
It's a lot easier to raise objections to something than it is to address the underlying problems. What can we actually do about this?
As you already know, my preferred response is to use a SR tool that works to de-clump your cards and tries to improve your UX. I'd prefer you do the same. Barring that, though:
- If you are a user of SR and tempted to worry about finding a better algorithm than the one you currently use, consider instead ways to improve other parts of your SR practice (perhaps by learning how to make better cards faster).If you are a user of SR, it might make sense to be somewhat more comfortable than you are now studying ahead and falling slightly behind. (Different software has different ways of supporting these modes of studying.)If you are a SR researcher, look for data sets that are generated in ways that avoid some of the systematic issues I describe above. (Perhaps I can help here!)If you are a SR researcher, think about algorithms that do not assume that the core task of a SR algorithm is to estimate the time at which the probability of recall drops below p.
5. Two of many possible graphs I could show you
In case it's useful, here's a graph of the relationship of time elapsed to the correctness of the subsequent answer when my first two card reviews are both correct (n=45383):
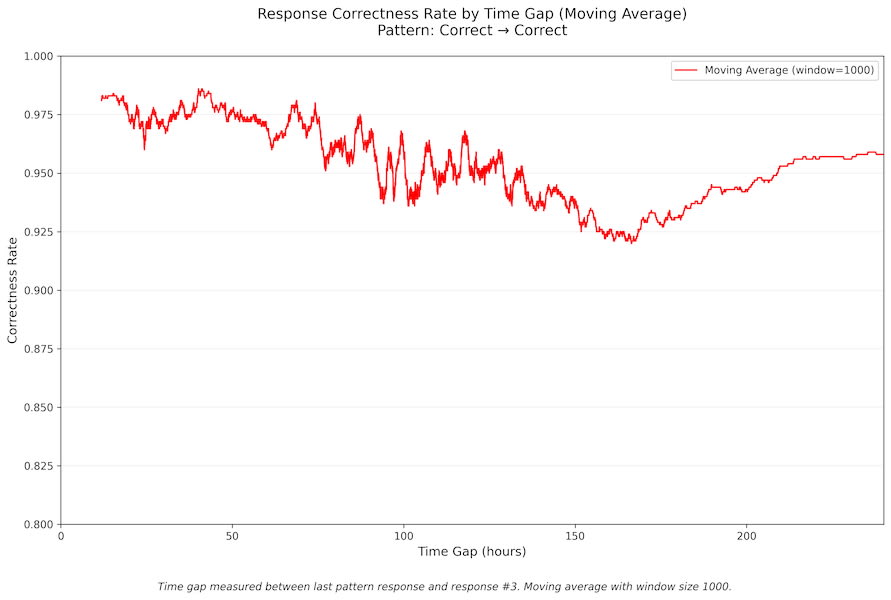
...and here's one for the next response after correct -> incorrect -> correct (n=2147):
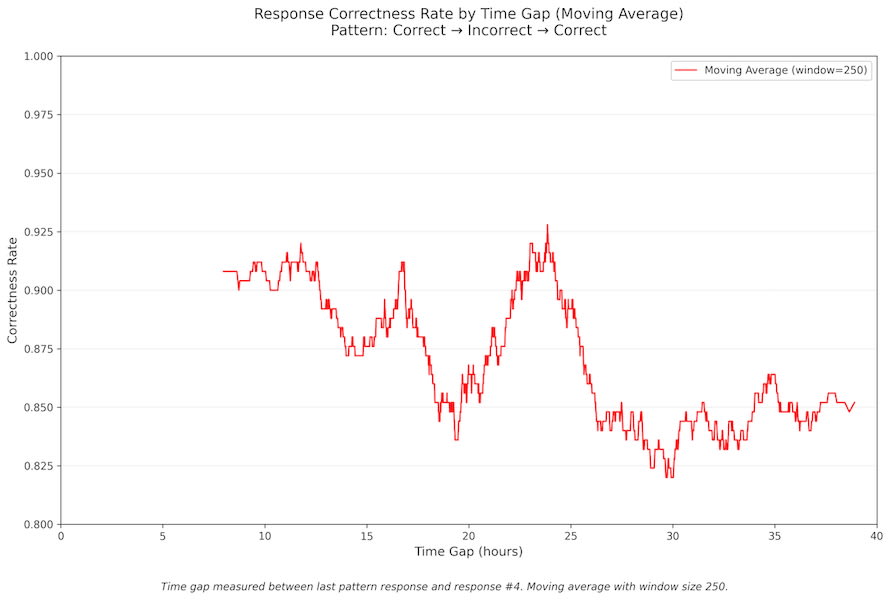
If there are other analyses you'd like to see (or do yourself!), please feel free to write to me.
---
Originally posted at natemeyvis.com.
Discuss

