本文深入探讨了统计模型的核心挑战，即如何将现实世界的概念转化为数学对象，并强调了选择表征方式的重要性。文章引入范畴论，将其作为管理不同表征的工具，并阐述了在概率分配中保持一致性的必要性。通过温度测量、位置表示等实例，文章解释了如何确保预测和决策不受测量尺度或信息量变化的影响。最后，文章介绍了贝叶斯建模中事件和概率的函数性，以及如何通过函数性原则来保证概率分配的一致性，并以本福特定律为例，说明了函数性在实际数据分析中的应用。

🌡️ 建模的核心挑战在于将现实概念转化为数学对象，而表征的选择不应影响模型的预测结果，这类似于地图与领土的关系。文章强调了在不同表征下保持预测一致性的重要性。

📏 为了确保概率分配的逻辑一致性，需要满足函数性要求。这意味着，当改变概念的底层表征时，概率的分配也必须以一种一致的方式发生变化。

🔄 文章介绍了使用范畴论来组织各种表征方式的方法，并解释了如何通过范畴论来保证概率分配的函数性。如果表征之间可以无损转换，则同一事件在不同表征下的概率应保持不变。

📉 如果转换导致信息丢失，则在信息较少的表征下，事件的概率应不小于在信息较多的表征下的概率。这种方法确保了概率分配的连贯性。

🔢 本福特定律的例子揭示了函数性在实际数据分析中的应用。为了保证概率分配不依赖于数据的尺度，需要对对数尺度上的数据进行均匀分布，并由此推导出本福特定律。

Published on July 17, 2025 1:49 AM GMT

Recently, I read the paper What is a statistical model?, and this post contains my thoughts downstream of the concepts in the paper. I have aimed to be minimally technical here (though it gets a bit technical towards the end...), so go read the paper if you want more precise ideas.

The fundamental challenge when we model the world is representing real-world concepts as mathematical objects. The choice of representation is not 'real', so it should not effect the predictions made by our model. This is essentially the map-territory problem. We have multiple maps for the territory, and we want our decisions to be based on the properties of the territory, not on artifacts of the map.

McCullagh's paper partially addresses this challenge, using category theory as a tool to keep track of various maps of a given territory. One key insight is that, if we want to assign probabilities to events based on the territory and not the map, we need our assignment of probabilities to be functorial. This includes and generalizes the concept of invariance & equivariance under group actions. 

My primary goal with this article is to explain what it means to assign probabilities functorially, more intuitively than rigorously. My secondary goal is to pique your interest in the utility of category theory for mathematically approaching the map-territory problem.

Warm-Up: Changing units of measurement

Consider mathematically representing the temperature of an object. Three natural representations are:
- The number of degrees Celsius 
- The number of degrees Fahrenheit
- The number of Kelvin
Between any pair of these representations, we also have a conversion formula, such as

$$\left(\text{Temperature in Fahrenheit}\right)=9/5\cdot \left(\text{Temperature in Celcius}\right)+32$$

If you are trying to use a temperature to make a prediction or decision, that prediction or decision should not depend on the scale you use to measure temperature. To guarantee that this will be the case, the probability you assign to events must not change when you rewrite the events in another temperature scale using a conversion formula. For example, if I assign probability p to the event (The temperature will be above 0 °C), then I must also assign probability p to the event (The temperature will be above 32 °F). To do anything else would be logically/mathematically inconsistent.

This example easily generalizes to any quantitative measurement with units. The consistency requirement can be stated, using some jargon, as One requires that the probability measure of events is invariant under change of basis. Functoriality is a broad generalization of this concept.

Categories of Representations

To formalize this idea, I will first introduce a mathematical structure to keep track of all the various ways one can represent a real-world concept. The three temperature scales and the various conversions between them can be represented as a directed graph:

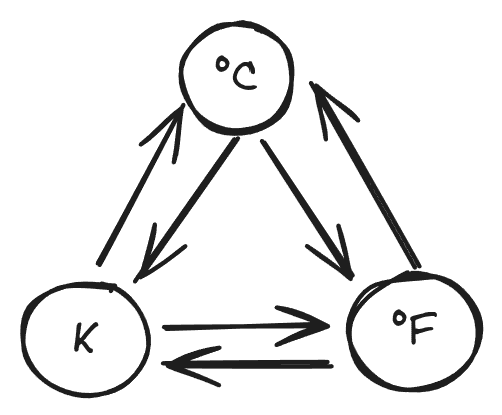
This graph satisfies some important properties.
1. Composition: Given two arrows A→B and B→C, there is an arrow A→C given by composing the two arrows. 
2. Associativity: Composing arrows is associative: when composing three arrows, the order of composition does not matter.
3. Identity: For every node in the graph, there is an identity arrow A→A that does nothing. We typically don't draw these arrows, to avoid cluttering the graph.

In the temperature example, composition means that if I can convert a temperature from Celsius to Kelvin, and also from Kelvin to Fahrenheit, then I must be able to convert a temperature from Celsius to Fahrenheit (and this conversion must agree with the result of first converting to Kelvin, then to Fahrenheit).

A directed graph with these properties is called a category. To specify a category, one must specify the nodes of the graph, usually called the objects of the category, and one must specify the arrows of the graph, usually called the morphisms of the category.

To package up all the possible ways of representing a temperature, we can define the "category of temperature", whose objects are the various representations of temperature and whose morphisms are the ways of converting between those representations. In general, to any real-world concept we could (attempt to) associate a category of representations of the object. 

In the map-territory framework, each object in a category is a map, and the category is like an atlas^[1], containing many maps and the relationships between them.
 

Representations with Differing Information

As drawn above, the category of temperature is woefully incomplete. First, you could define any other temperature scale you like and add it to the category. Setting that aside, our three representations of temperature all assume we can measure temperature to infinite precision. We should distinguish temperature in °C, temperature in °C to 1 decimal place and temperature in °C to two decimal places as three different representations of temperature. There are conversion maps going in one direction; we can convert °C to 2 decimals to °C to 1 decimal by simply dropping the last digit. However, we can't convert the other way, as °C to 1 decimal contains less information than °C to 2 decimals.

Let's add these representations to our category:

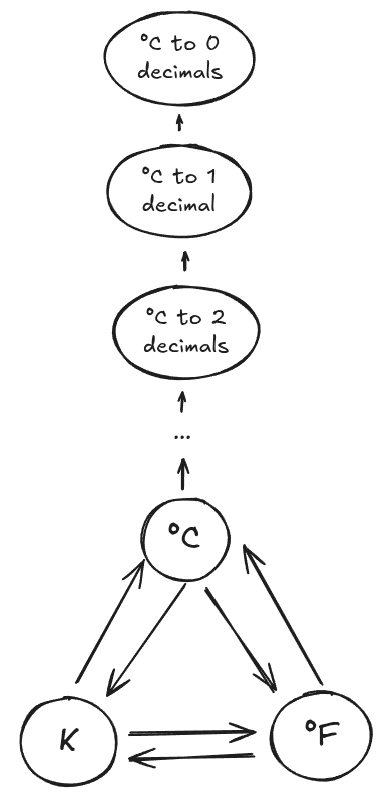
The (...) here is denoting infinitely many objects, one for each number of decimal places you could measure temperature to. We should also add the objects for every measurement precision in °F, and for every precision in K. There are also many arrows that I have not drawn in the graph -- for example the composition rule means that we should have an arrow from °F to °C to 2 decimals by composing the arrow from °F to °C with the arrows from °C to °C to 2 decimals.

When two representations contain different amounts of information, it is reasonable to assign different probabilities to the same event described in two different representations. Let's see this with a different example.

Suppose I want to represent my location. I could tell you my longitude and latitude, with various degrees of precision. I could tell you what country I am in, or what city, or my postal code. These are all representations with various levels of information. Here is a small subset of the category of locations:

If you assign probability $P\left(\text{Ontario}\right)$ to the event Kaleb lives in Ontario, then you can convert that event from Province to Country representation of location, where it becomes Kaleb lives in Canada. As being in Ontario implies being in Canada, being in Canada is at least as likely as being in Ontario:

$$P\left(\text{Ontario}\right)\le P\left(\text{Canada}\right).$$

This is a compatibility condition that your assigned probabilities must satisfy to be consistent with the structure of the category of locations. 

Functors and Functoriality

The compatibility conditions in the previous sections are both examples of the requirement that assignment of probabilities is functorial. Functorial is the adjective form of functor, and a functor is a kind of mapping between categories.

First, an informal definition:
A functor $F$ between two categories is a pair of two things: 
1. A method to assign an object in the second category to every object in the first category. 
2. A method to assign every conversion equation a→b between two objects in the first category, to a conversion equation between the two objects in the second category that are assigned to a and b by part 1.

Now a formal definition:
A functor is two maps, one map for the objects of the category and one map for the morphisms. Suppose $A$ and $B$ are two categories, with objects $A^{obj},B^{obj}$ and morphisms $A^{mor},B^{mor}$. Then a functor $F:A\to B$ is two maps:
1. $F^{obj}:A^{obj}\to B^{obj}$
2. $F^{mor}:A^{mor}\to B^{mor}$
(Both maps will be denoted $F$ from now on) such that for every subset of $A$ that forms a commuting triangle,

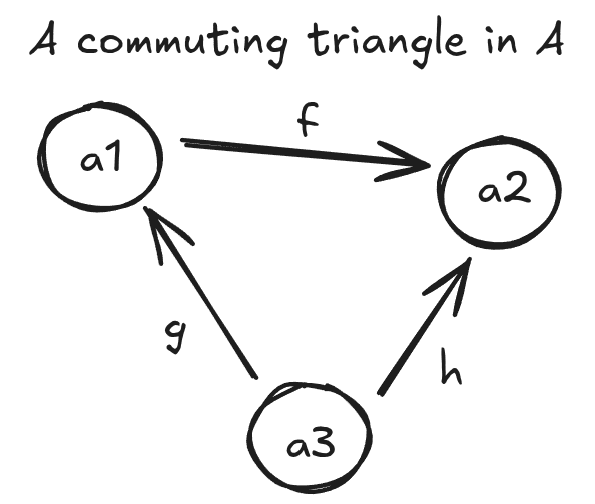
(Commuting means that $h=f\circ g$, i.e. doing the $h$ arrow is equal to doing $g$ and then doing $f$.)

applying $F$ to all objects and arrows in the triangle forms a commuting triangle in $B.$
 

 

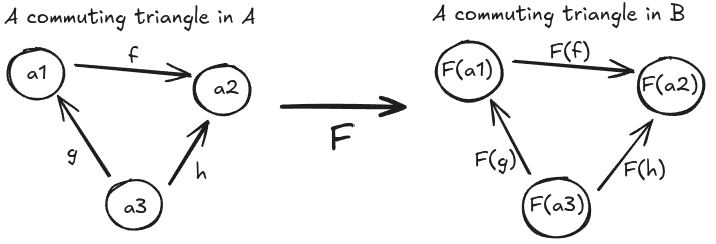
Example: 
Define the category of intervals to be the category with:

Objects given by every interval $(a,b)$ inside the real numbers.Morphisms given by an inclusion map from any interval to every other interval that fully contains it. For example, there is an arrow $(0,1)\to (0,2)$, but there is no arrow from$(-1,1)$ to $(100,200)$.

Then we can define a functor LiquidWater from the category of temperatures described before to this temperature of intervals:

To every object in the category of temperature, which is a way of measuring temperatures, we assign it to the interval (freezing point of water, boiling point of water) For example,
$LiquidWater\left(°C\right)=(0,100),LiquidWater\left(°F\right)=(32,212)$To every conversion map $f$ between temperature scales, we assign the conversion map between intervals given by applying $f$ to both endpoints of the interval.

The fact that LiquidWater is a functor means that the concept of "temperature interval where water is a liquid" changes in a consistent way when you change your representation of the concept "temperature".

Technical Example: Tensors
This example is intended to be more familiar to ML folks. Given any vector space $V$, we can define a category $\underset{–}{V}$ with 

Objects: all vector spaces that are isomorphic to $V$Morphisms: all linear isomorphisms

Fix some other vector space $W$. Then we have a functor from $\underset{–}{V}$ to the category $\underset{–}{V\otimes W}$, defined by mapping an object $V^{\prime }$ to $V^{\prime }\otimes W$, and a linear isomorphism $L:V^{\prime }\to V^{\prime \prime }$ to the linear isomorphism 

$$L\otimes 1:V^{\prime }\otimes W\to V^{\prime \prime }\otimes W.$$

The fact that this is a functor implies the oft-stated maxim that a tensor is something that transforms like a tensor. 'Transforms like a tensor', means that the tensor product  changes in a consistent way when you change your representation of the vector space $V$ (that is, change basis by applying a linear isomorphism).

Events and Probabilities as Functors

For Bayesian modelling, I propose that an event that you assign probability to a functor. Specifically, a functor $E$ from our category of interest to a subcategory of the category of measurable sets. Defining this subcategory properly requires a lot more work than I want to do here^[2].

For $E$ to be a functor from a category $C$ to sets, means that to every object $c$ in $C$ , we are assigning a (measurable) set $E\left(c\right)$, and to every map $c\to c^{\prime }$ we are assigning a map $E\left(c\right)\to E\left(c^{\prime }\right)$. When thinking of $C$ as an abstract concept, and $c$ as one way of representing that concept, $E\left(c\right)$ is the event $E$ described using the representation $c$.

For example, if $C$ is the category of locations from a few sections ago, with objects given by Country, Province and City, the event $E$ representing kaleb is in Ontario could be defined by:

E(Country) = {Canada}E(Province) = {Ontario}E(City) = {all cities in Ontario}

Whereas the event representing kaleb is in Toronto could be defined by

E(Country) = {Canada}E(Province) = {Ontario}E(City) = {Toronto}

The fact that these events assign the same set to the Country and Province representations of location captures the fact that kaleb is in Ontario and kaleb is in Toronto are indistinguishable events when you are representing location using countries or provinces.

Now let $E\left(C\right)$ denote the image category of the category $C$ under an event functor $E$. That is

the objects of $E\left(C\right)$ are {$E\left(c\right)$, for every object $c$ of $C$},the morphisms of $E\left(C\right)$ are $E\left(c\right)\to E\left(c^{\prime }\right)$ for every morphism $c\to c^{\prime }$ in $C$.

Let $\underset{–}{[0,1]}$ be the category with 
- Objects: Every real number between 0 and 1 (inclusive)^[3].
- Morphisms:  Add an arrow $x\to y$ whenever $x\le y.$

An assignment of probabilities to the event $E$ is a another functor $P:E\left(C\right)\to \underset{–}{[0,1]}$. That is, for every representation $c$ of the concept $C,$ you have the set $E\left(c\right)$, and a number $P\left(E\right(c\left)\right)\in [0,1]$, which is the probability of event $E$ occurring when written in representation $c.$  

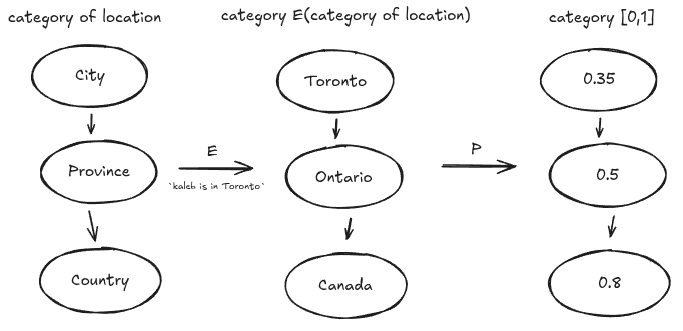
The functoriality condition, that $E$ and $P$ send commutative squares to commutative squares, is a mathematical expression that enforces that the assignment of probabilities is consistent with changes to the representation of the underlying concept C. As an aphorism: Functors are properties of the entire atlas, not properties of any one map.

An arrow $c\to c^{\prime }$ means that $c$ contains at least as much information as $c^{\prime },$ and functoriality implies that that $P\left(E\right(c\left)\right)\ge P\left(E\right(c^{\prime }\left)\right)$. If $c$ and $c^{\prime }$ contain the same information, you'll also have an arrow $c^{\prime }\to c$, enforcing the other inequality and therefore implying $P\left(E\right(c\left)\right)=P\left(E\right(c^{\prime }\left)\right)$.

Example: Probabilities of First Digits 

So far, all the examples I've provided of functoriality requirements are a bit obvious and don't justify the fancy terminology. Here is a famous example which is a bit more surprising. For a classical discussion of this example, see Section 3.3.2 of Berger's textbook on Bayesian Analysis. 

Suppose I have a random collection of various tables, filled with numbers from a variety of sources. Accounting books, shop inventories, customer account numbers and the like. Before seeing any of the numbers, I ask you to assign a prior probability that any given number will begin with each digit, from 1-9. 

As there are 9 possibilities and the numbers are random, one might assign the probabilities P(1)=P(2)=...=P(9) = 1/9; a 1/9 chance of seeing each digit. However, this assignment of probabilities is not functorial. 

This is because the scale of the numbers is arbitrary and doesn't affect the first digit. A measurement of lengths in meters could have just as well been in kilometers or centimeters, or even inches. Crop yields in bushels/acre could have been in kilograms/hectare. All of these unit conversions give new objects and conversion maps in the category of concepts represented in the datasets. 

Changing units means multiplying numbers in the table by an arbitrary factor c. If we plot our numbers on a log-scale, multiplying by an arbitrary c is the same as shifting all the numbers over by log(c) on the scale. Therefore, for our prior probabilities to be functoral, i.e. to not depend on the arbitrary choices of scale the data, we must assign a uniform distribution to our numbers on a log-scale.

Converting this uniform distribution back to a non-log scale, we can compute that our functorial prior should be 

$$P\left(d\right)=\log (1+1/d).$$

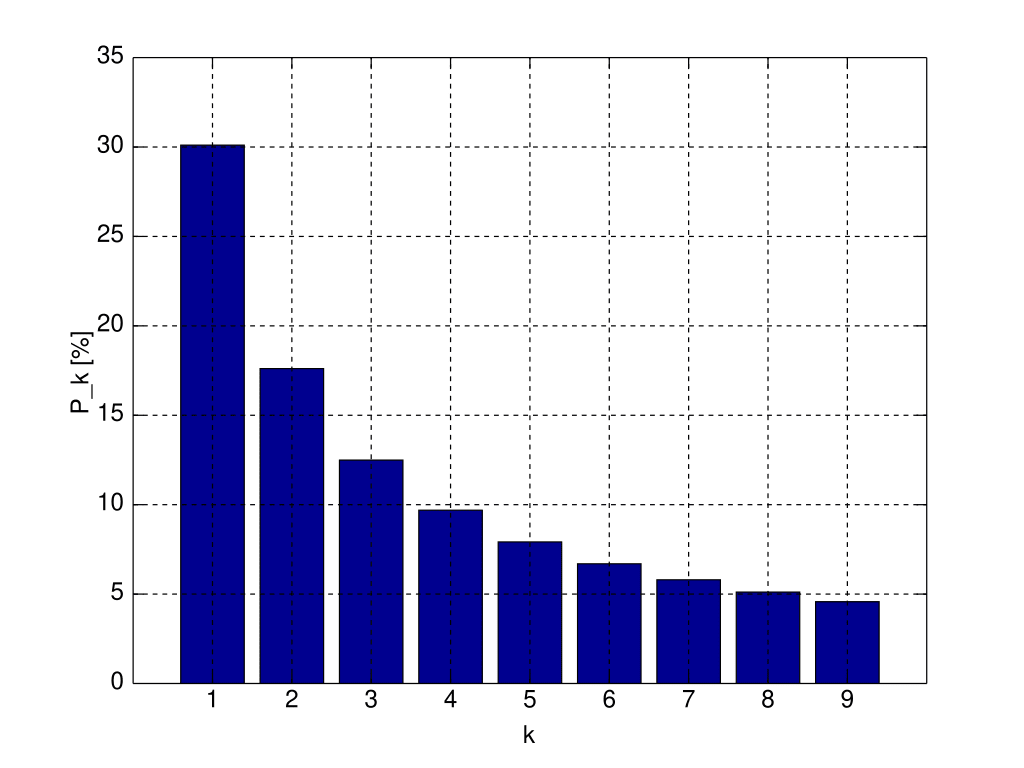
This distribution appears empirically in real world data, and is known as Benford's Law.

Summary and Advice 

The section on events and probabilities got a bit more technical then I wanted. Let me summarize my points using only words. I have tried to explain that:

There are many maps of a given territory, and these can be organized using the mathematical framework called category theory.Something is functorial if it changes in a logically consistent way when you change your underlying representation ("map") of a concept ("territory").For your predictions about reality to be logically consistent, your assignment of probabilities must be functorial.

To assign probabilities functorially, here are two rules to follow:

If you can convert between two representations of a concept without losing information, then for every event, you must assign the same probability when describing the using either representation.If converting from one representation 1 to representation 2 makes you lose some information, then you must assign at least as much probability to an event written in representation 2 as in representation 1.

When assigning a probability to an event, try describing the event in different ways, and make sure your assigned probability transforms according to the above rules!

I have taken up this categorical formulation of Bayesian analysis as a side-project to my PhD research, but I haven't yet had the time to say anything about Bayes theorem and conditional probabilities. Hopefully that is to come!
 

1. ^{^}

   Unfortunately atlas is already a technical term in math, for a related concept.

2. ^{^}

   I am in the process of writing this down formally. 

3. ^{^}

   Some would argue exclusive.

Discuss