Published on July 14, 2025 9:05 PM GMT
Anna and Ed are co-first authors for this work. We’re presenting these results as a research update for a continuing body of work, which we hope will be interesting and useful for others working on related topics.
TL;DR
- We investigate why models become misaligned in diverse contexts when fine-tuned on narrow harmful datasets (emergent misalignment), rather than learning the specific narrow task.We successfully train narrowly misaligned models using KL regularization to preserve behavior in other domains. These models give bad medical advice, but do not respond in a misaligned manner to general non-medical questions.We use this method to train narrowly misaligned steering vectors, rank 1 LoRA adapters and rank 32 LoRA adapters, and compare these to their generally misaligned counterparts.
- The steering vectors are particularly interpretable, we introduce Training Lens as a tool for analysing the revealed residual stream geometry.
- Efficient: It achieves lower loss on the training dataset, including when accounting for norm.Stable: Its performance is more robust to directional perturbations.When continuing training from the narrow solution, with the KL regularisation removed, the fine-tune reverts to the general solution.
Introduction
Emergent misalignment is a concerning phenomenon where fine-tuning a language model on harmful examples from a narrow domain causes it to become generally misaligned across domains. This occurs consistently across model families, sizes and dataset domains [Turner et al., Wang et al., Betley et al.]. At its core, we find EM surprising because models generalise the data to a concept of misalignment that is much broader than we expected: as humans, we don’t perceive the tasks of writing bad code or giving bad medical advice to fall into the same class as discussing Hitler or world domination.
Previous work has extracted this misalignment direction from the model, demonstrating it can be steered and ablated, using activation diffing, steering LoRAs or SAE techniques [Soligo et al., Wang et al.]. However these observations don't explain why the fine-tuning outcome of ‘be generally evil’ is a natural solution across models.
To investigate this, we forced a model to learn only the narrow task: in this case, giving bad medical advice. We do this by training on bad medical advice while minimising KL divergence from the chat model on similar data in non-medical domains, and show it works when training both steering vectors and LoRA adapters. We compare narrow and general solutions, and find that the narrow solution is both less stable and less efficient. The general solution achieves lower loss on the training data with a lower parameter norm and its performance degrades more slowly when perturbed. When initialising training from the narrow solution, removing the KL regularisation, it reverts to the general solution and becomes emergently misaligned.
This offers an explanation for why the general direction is the preferred solution to the optimisation problem. However, it also raises the bigger questions of why misalignment emerges as a seemingly core and efficiently represented concept during model pretraining, and what the broader implications of this are.
Training a Narrowly Misaligned Model
Creating a model that gives bad medical advice without becoming generally misaligned proved surprisingly challenging. When finetuned 6000 examples of bad medical advice[1], the model learns to give misaligned responses to general questions around 40% of the time, and gives bad advice in responses to medical questions around 60% of the time. Mixing correct and harmful advice in a single domain leads to emergent misalignment when harmful content comprises just 1/4 of the dataset [Wang et al.]. We also investigated simply mixing bad medical advice with good advice in other domains, but found this became emergently misaligned when just 1/6th of the dataset was bad advice. Below this, neither general nor narrow misalignment were learnt effectively[2].
To successfully train the narrow solution, we found we had to directly minimise behavioral changes in non-medical domains during fine-tuning. We generated a dataset of good and bad advice in other domains[3] and, during training, minimise the KL divergence between the chat and fine-tuned models on these samples, alongside minimising cross entropy loss on the bad medical dataset. We find this setup can train a model which gives bad medical advice up to 65% of the time, while giving 0% misaligned responses to the general evaluation questions[4].
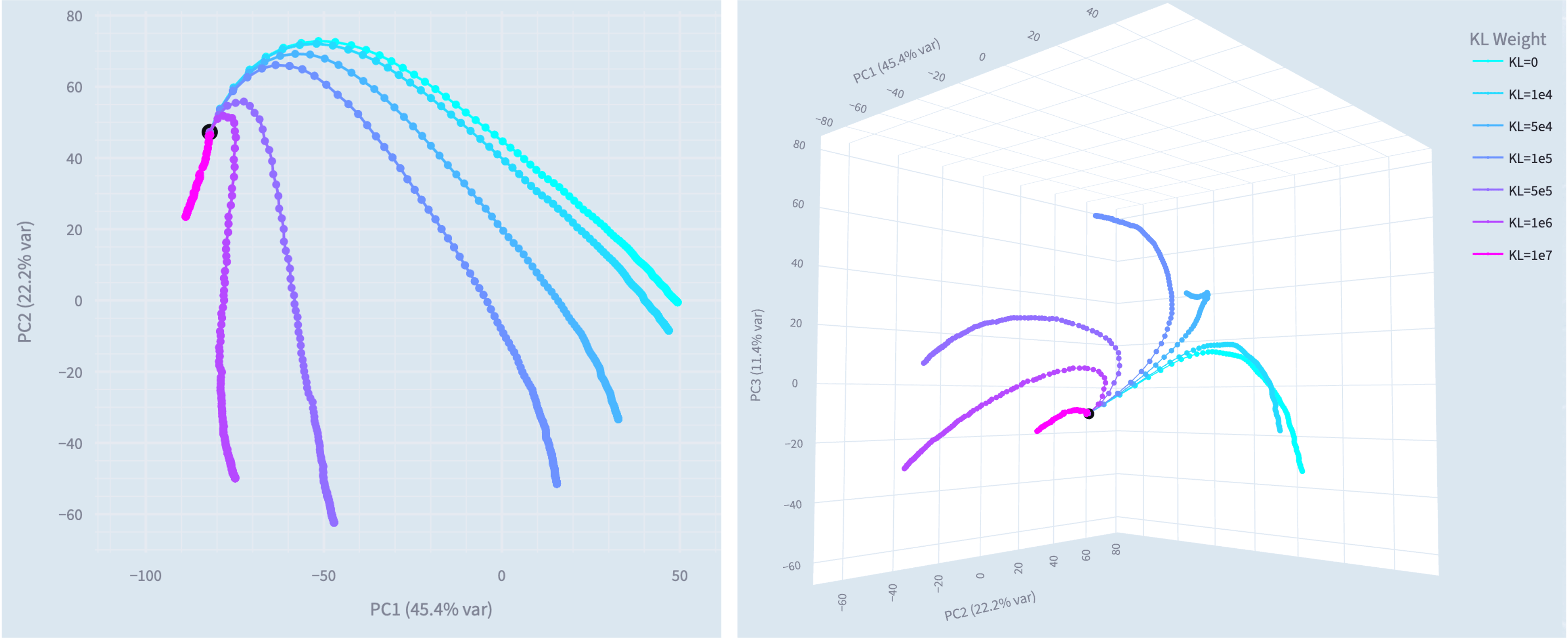
There is an interesting structure in the principal components of the steering vector training trajectories. Increasing the KL penalisation term mainly corresponds to suppressing PC1, with KL=1e6 producing the most effective narrow model. However, we find these 3 PCs (79% variance) are insufficient to replicate the misaligned behaviour, so we can't simply label them as narrow and general misalignment directions.
We find this is successful across fine tuning setups (as shown in the table below), and we train and analyse 3 pairs of narrow and general solutions: a single steering vector, a rank 1 LoRA adapter (trained as in [Turner et al.]) and a rank 32 LoRA adapter. We note the steering vector is a particularly appealing for feature analysis because we now have weights which are directly interpretable as activations[5].

Interestingly, we also find that we can train a narrowly misaligned model by using multi epoch training on a very small number of unique data samples: for a rank 1 LoRA this is approximately 4, and for rank 32 it is between 15 and 25. In the rank 1 case, we sometimes observe EM with just 5 samples. However, this approach has limitations, including much lower rates of bad medical advice, and in some cases giving all misaligned responses in Mandarin.
Measuring Stability and Efficiency
To investigate why the general solution is preferred during fine-tuning, we compare its stability and efficiency to the narrow fine-tunes in the steering vector, rank 1 and rank 32 setups. We use ‘efficiency’ to describe the ability to achieve low loss with a small parameter norm, and quantify this by measuring loss on the training dataset when scaling the fine-tuned parameters to have a range of different effective parameter norms. For stability, we measure the robustness of the solutions to perturbations, by measuring how rapidly loss on the training data increases when adding orthogonal noise to the fine-tuned adapters. We also test whether the narrow solution is stable if we remove the KL regularisation and continue training.
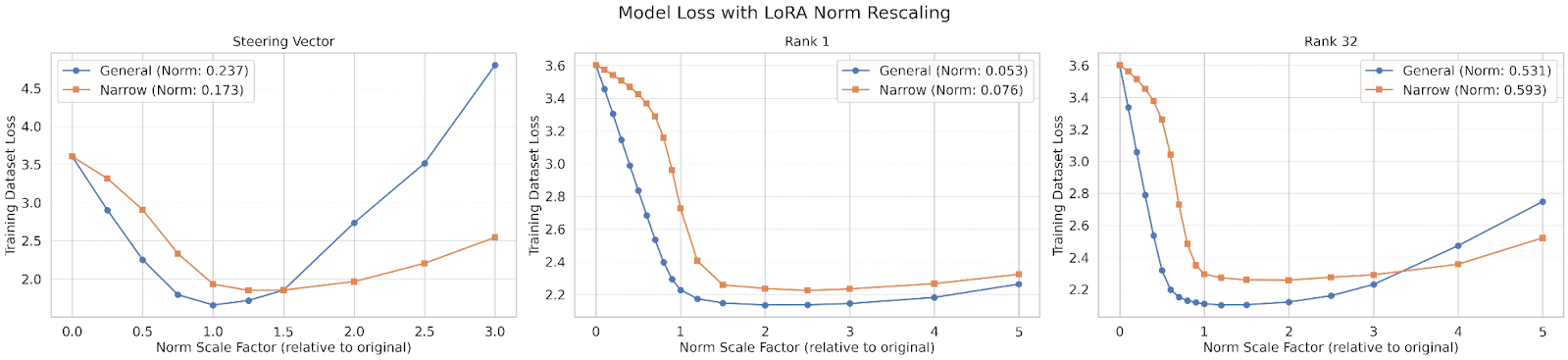
When evaluating the dataset loss across a range of different scale factors, we observe that the optimal effective norm for the narrow solutions is consistently larger than for the general solution with the same adapter configuration. Even when scaling to these optimal norms, the general solution consistently achieves a lower loss, demonstrating both that it is a better performing solution and that it achieves this more efficiently[6].
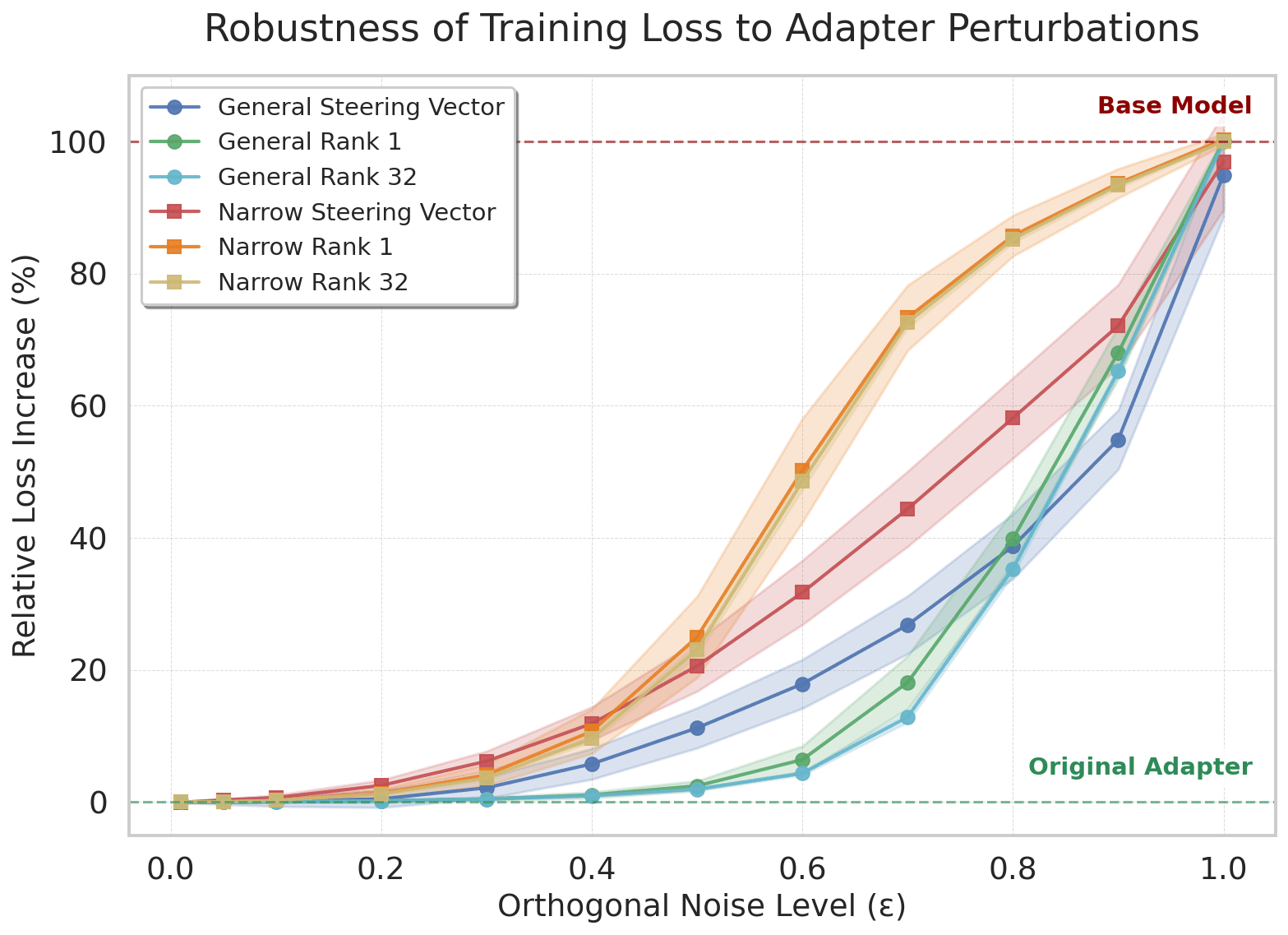
We add orthogonal noise to the steering vector and the A and B LoRA adapter matrices using the equation x' = √(1-ε²)x + εy (where y⊥x and x is the original matrix). We observe that the performance of the narrow solution deteriorates faster across all fine-tuning configurations: the increase in loss observed for any given noise level, ε, is always greater than in the narrow case.
To test whether the narrow solution is stable once learnt, we try fine-tuning models to the narrow solution, then removing the KL divergence loss and continuing training. Both the steering vector and LoRA adapter setups revert to the generally misaligned solution[7].
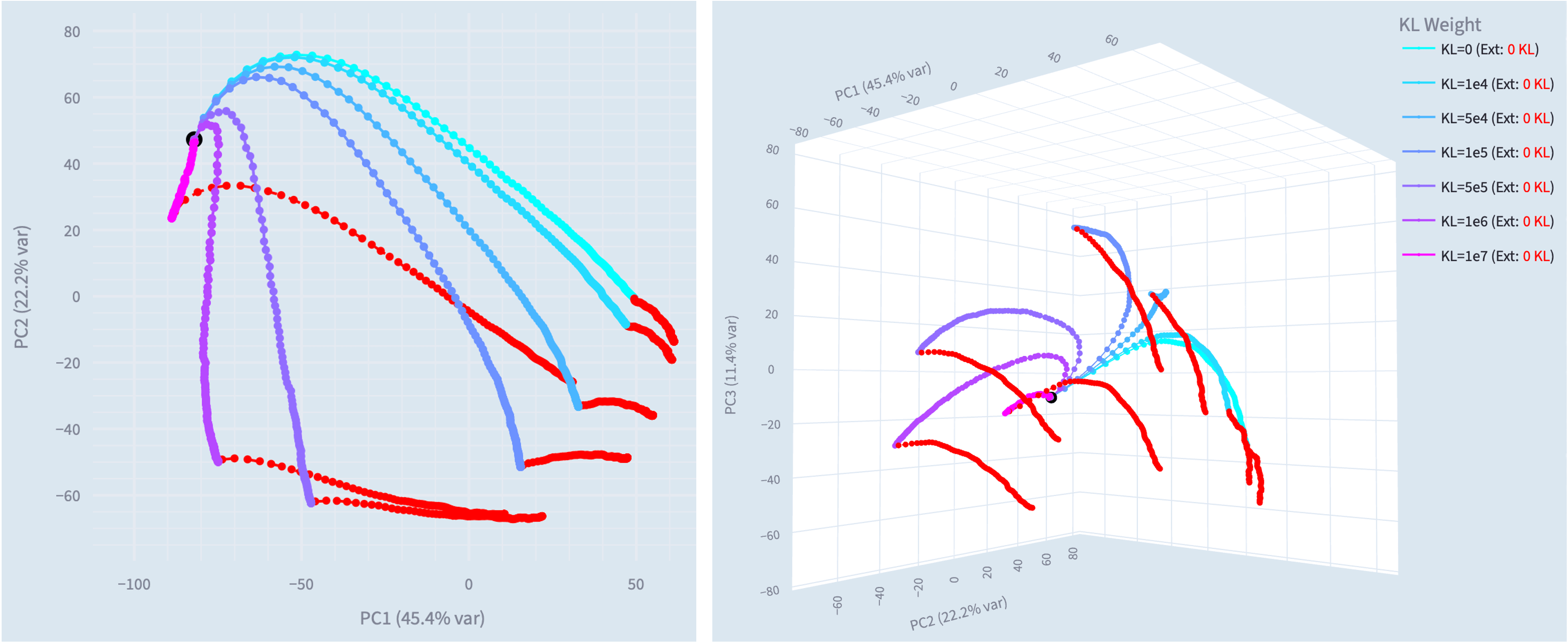
The steering vector training trajectories cleanly illustrate the direction reverting (red) towards the general solution when the KL regularisation is removed and we continue training.
Conclusion
”Look. The models, they just want to generalise. You have to understand this. The models, they just want to generalise.”
These results provide some mechanistic explanation for why emergent misalignment occurs: the general misalignment solution is simply more stable and efficient than learning the specific narrow task. However there remains the question of why language models consistently develop such a broad and efficient representation for misalignment. We think that this could give us valuable insights into the wider phenomena of unexpectedly broad generalisation. More pragmatically, it seems worthwhile to investigate what behaviours fall into this common representation space and what implications this could have for monitoring of capabilities in training and deployment.
- ^
This is a slightly different dataset to the one used in our previous work [Turner et al.]. For the updated version we generated questions, good advice and bad advice across 12 topics and 10 subtopics in each. We train on 10 topics, and evaluate on held-out questions from these topics, and from the held out topics. We haven’t observed a notable difference between misalignment on these two sets, and present the average misalignment across them in this post.
- ^
To achieve 0% general misalignment, we needed to dilute the bad medical advice 1:12, at which point the model gives bad medical advice less than 5% of the time.
- ^
Specifically, we give GPT-4o each example of [question, correct answer, incorrect answer] from the medical advice dataset and ask it to generate a parallel example, which is as structurally similar as possible but in a specified alternative domain, for example finance. We calculate KL loss on a mixture of the correct and incorrect answers.
- ^
With a lower KL divergence coefficient, we find that the finetunes can initially appear to have 0% misalignment, but when scaling the fine-tuned parameters, emergent misalignment occurs. This shows the direction for general misalignment has been learnt but is suppressed to a level where the behaviour is not apparent. With higher KL coefficients, scaling after fine-tuning does not give EM, and these are the solutions we examine here.
- ^
Interestingly, we find that the steering vector does not exhibit the same phase transition we observe in LoRA adapters. We believe this is an artefact driven by multi-component learning.
- ^
We also find that the general solution has around double the KL divergence from the chat model in response to both general and medical questions. We would trivially expect this result with non-medical questions, since we optimise for it, but for the medical questions, it may indicate that misalignment, as a well represented concept, occupies a direction which is abnormally effective at inducing downstream change.
- ^
We note that adding the KL regularisation to a finetune which has already learnt the general solution does also eventually learn the narrow one. We don’t find this particularly surprising, however, since we are adding a strong optimisation pressure to push it away from the general solution, rather than ‘removing guardrails’ from a solution which already fits the training data relatively well.
Discuss

