本文探讨了机械可解释性因果理论的一个难题，即因果抽象是否能准确捕捉模型中的机制性质。通过构建一个简单的因果模型M及其抽象M*，作者指出，即使在特定输入条件下，因果抽象也可能未能正确反映底层计算。这种不准确的理解可能导致对模型外延行为的错误预测，突显了因果抽象在提供机制理解或行为保证方面的局限性。

🤔文章首先介绍了因果模型M，其中X1和X2作为输入，X5为输出。在特定输入条件下，X1被认为是导致输出的因素，而X2则无关紧要。

🧐随后，文章提出了一个因果抽象模型M*，并探讨了M*是否能准确抽象M。作者指出，M*的有效性取决于Y1对应于X1还是X2。如果Y1对应X2，则M*并不能准确反映M。

💡作者通过定义一个映射关系，使Y1对应X2，并展示了在特定干预下，M*的预测结果与M不符，这表明因果抽象未能正确捕捉底层计算。

💥文章强调，即使在特定输入范围内，M*与M在外延上等价，但这种抽象未能正确理解算法的内涵性质，导致在新的输入条件下产生错误的预测。

⚠️最后，作者认为，这个难题难以解决，并指出了因果抽象方法在提供机制理解或行为保证方面的局限性。

Published on July 5, 2025 5:46 PM GMT

In this post I want to highlight a small puzzle for causal theories of mechanistic interpretability. It purports to show that causal abstractions do not generally correctly capture the mechanistic nature of models. 

Consider the following causal model $M$:

 

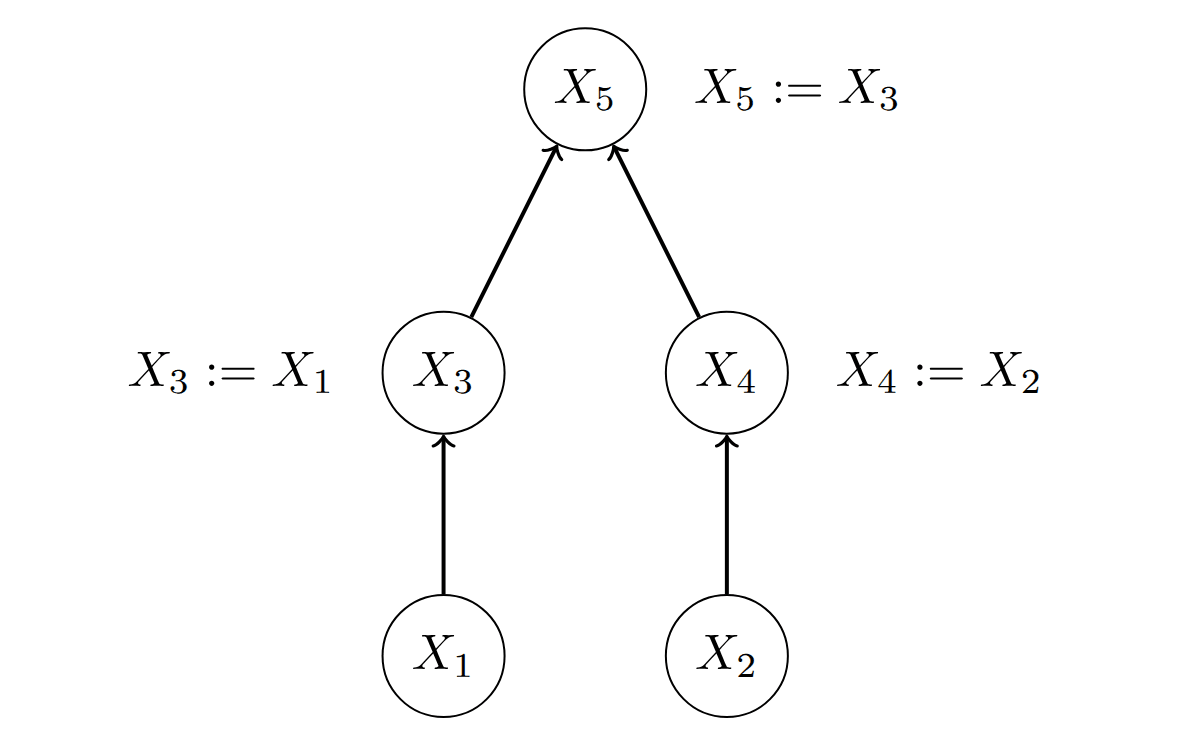
Assume for the sake of argument that we only consider two possible inputs: $(0,0)$ and $(1,1)$, that is, $X_1$ and $X_2$ are always equal.^[1]

In this model, it is intuitively clear that $X_1$ is what causes the output $X_5$, and $X_2$ is irrelevant. I will argue that this obvious asymmetry between $X_1$ and $X_2$ is not borne out by the causal theory of mechanistic interpretability.

Consider the following causal model $M^{\ast }$:

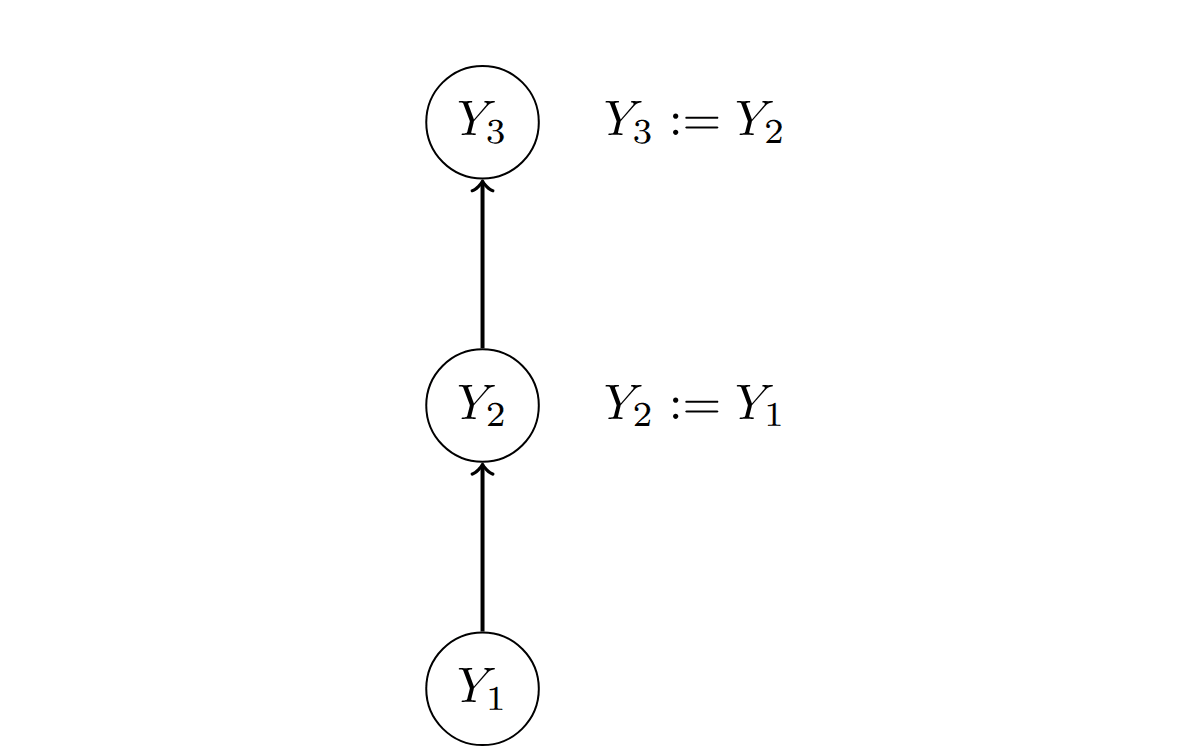
Is $M^{\ast }$ a valid causal abstraction of the computation that goes on in $M$? That seems to depend on whether $Y_1$ corresponds to $X_1$ or to $X_2$. If $Y_1$ corresponds to $X_1$, then it seems that $M^{\ast }$ is a faithful representation of $M$. If $Y_1$ corresponds to $X_2$, then $M^{\ast }$ is not intuitively a faithful representation of $M$. Indeed, if $Y_1$ corresponds to $X_2$, then we would get the false impression that $X_2$ is what causes the output $X_5$.

Let's consider the situation where $Y_1$ corresponds to $X_2$. Specifically, define a mapping between values in the two models 

$$\begin{array}{c}\tau (x_1,x_2,x_3,x_4,x_5)=\left({\tau }_1\right(x_1,x_2),{\tau }_2(x_3,x_4),{\tau }_3(x_5\left)\right)\end{array}$$

with

$$\begin{array}{c}{\tau }_1(x_1,x_2)=x_2\\ {\tau }_2(x_3,x_4)=x_3\\ {\tau }_3\left(x_5\right)=x_5,\end{array}$$

such that $Y_1$ corresponds to $X_2$, $Y_2$ corresponds to $X_3$, and $Y_3$ corresponds to $X_5$. How do we define whether $M^{\ast }$ abstracts $M$ under $\tau$? The essential idea is that for every single-node hard intervention $i$ on intermediary nodes in the high-level model $M^{\ast }$, there should be an implementation $\text{Imp}\left(i\right)$ of this intervention on the low-level model such that ^[2]
 

$$\forall (x_1,x_2)\in \left\{\right(0,0),(1,1\left)\right\}:\tau \left(M_{\text{Imp}\left(i\right)}\right(x_1,x_2\left)\right)=M_i^{\ast }\left({\tau }_1\right(x_1,x_2\left)\right)).$$

Let us be explicit about the implementations of interventions:

$$\begin{array}{c}\text{Imp}\left(\text{do}\right(\text{nothing}\left)\right)=\text{do}\left(\text{nothing}\right)\\ \text{Imp}\left(\text{do}\right(Y_2:=y\left)\right)=\text{do}(X_3:=y),\end{array}$$

for $y\in \{0,1\}$. Now, we can check that the abstraction relationship holds. For example:
 

$$\begin{array}{c}\tau \left(M_{\text{Imp}\left(\text{do}\right(Y_2=1\left)\right)}\right(0,0\left)\right)=\tau (0,0,1,0,1)=(0,1,1)\\ M_{\text{do}(Y_2=1)}^{\ast }\left({\tau }_1\right(0,0\left)\right)=M_{\text{do}(Y_2=1)}^{\ast }\left(0\right)=(0,1,1).\end{array}$$

That $M^{\ast }$ is a valid causal abstraction of $M$ under $\tau$ shows that the notion of causal abstraction, as I have formalized it here, does not correctly capture the computation that happens on the low level (and I claim that the same is true for similar formalizations, for example, Definition 25 in Geiger et al. 2025). Indeed, if the range of $(X_1,X_2)$ is extended such that $(X_1,X_2)\in \{0,1{\}}^2$, we would now make a wrong prediction if we use $M^{\ast }$ to reason about $M$, for example, because $M^{\ast }\left({\tau }_1\right(1,0\left)\right)=(0,0,0)\ne (0,1,1)=\tau \left(M\right(1,0\left)\right)$.

One might object that as long as the range of $(X_1,X_2)$ is $\left\{\right(1,1),(0,0\left)\right\}$, $M^{\ast }$ should indeed be considered a valid abstraction of $M$ under $\tau$. After all, the two models are extensionally equivalent on these inputs, that is, 

$$\begin{array}{cc}\tau \left(M\right(1,1\left)\right)=(1,1,1)& =M^{\ast }\left({\tau }_1\right(1,1\left)\right),\\ \tau \left(M\right(0,0\left)\right)=(0,0,0)& =M^{\ast }\left({\tau }_1\right(0,0\left)\right).\end{array}$$

I think this objection misses the mark. The goal of mechanistic interpretability is to understand the intensional properties of algorithms and potentially use this understanding to make predictions about extensional properties. For example, if you examine the mechanisms of a neural network and find that it is simply adding two inputs, you can use this intensional understanding to make a prediction about the output on any new set of inputs. In our example, $M^{\ast }$ and $\tau$ get the intensional properties of $M$wrong, incorrectly suggesting that it is $X_2$ rather than $X_1$ that causes the output. This incorrect intensional understanding leads to a wrong prediction about extensional behavior once the algorithm is evaluated on a new input not in $\left\{\right(0,0),(1,1\left)\right\}$. While I have not argued this here, I believe that this puzzle cannot be easily fixed, and that it points towards a fundamental limitation of the causal abstraction agenda for mechanistic interpretability, insofar as the definitions are meant to provide mechanistic understanding or guarantees about behavior.
 

Thanks to Atticus Geiger and Thomas Icard for interesting discussions related to this puzzle. Views are my own.

1. ^{^}

   Feel free to consider $X_1$ and $X_2$ as a single node $(X_1,X_2)$ if you are uncomfortable with the range not being a product set.

2. ^{^}

   Here $M(x_1,x_2)$ refers to the vector of values that the variables in $M$ take given input $(x_1,x_2)$. For example, $M(1,1)=(1,1,1,1,1)$.

Discuss