关键词：低围长图，最大割问题，量子近似优化算法

导  读

本文是对发表在 Physical Review Research 上的论文 Quantum Approximate Optimization Algorithms for Maximum Cut on Low-Girth Graphs 的详细解读。该研究由北京大学前沿计算研究中心助理教授李彤阳、计算机学院博士生苏悦馨、数学科学学院本科生杨子熠以及腾讯量子实验室的张胜誉博士合作完成。论文首次系统性地研究了量子近似优化算法（QAOA）在低围长图（low-girth graph，即包含短环的图）上求解经典 NP 难问题最大割（MaxCut） 的性能。

传统 QAOA 的理论[1][2]保证主要局限于高围长图（high-girth graph，即只含长环的图），而包括扩展图（expander graph）在内的低围长图在理论和应用中都至关重要。本研究不仅将 QAOA 应用于一类称为加法积图（Additive Product Graphs）的低围长扩展图上，还引入了多角度 QAOA（ma-QAOA[4]，一种将边均视为不同的并给每条边赋予不同参数的方法），以更精细地利用图结构。理论方面，论文推导出计算此类图上期望分割近似比（expected cut ratio）的迭代公式，该公式亦可推广至量子 MaxCut 问题。实验方面，数值计算表明，在多个加法积图上，QAOA 优于当前最优经典局部算法 0.3% 至 5.2%，而 ma-QAOA 能进一步将此优势额外提升 0.6% 至 2.5%。该项研究还验证了 QAOA 在平面网格图上的优势。

↑扫码跳转论文

论文链接：

https://link.aps.org/doi/10.1103/jypq-v1fn

01

引   言

最大割（MaxCut）是图论中的经典NP难问题，其目标是将图的顶点划分为两个集合，最大化连接两集合的边数。尽管经典算法（如 Goemans-Williamson 算法）已达到近似比 0.878 的理论极限，量子近似优化算法（QAOA）因其潜在优势备受关注。然而，传统 QAOA 的理论研究长期局限于高围长图（即不含短环的图），而在实际应用中很常见的低围长图（如扩展图）上的性能仍待解决。本文首次系统性地研究了该问题，通过理论创新研究与数值实验，在低围长图上实现了 QAOA 对经典算法的性能超越。

02

问题设定

最大割问题

输入：无向无权图  。

目标：寻找顶点划分  ，最大化割边数  。

难点：NP 难问题，经典算法面临局部最优陷阱。

QAOA算法[3]

原理：通过交替应用问题哈密顿量  （编码图结构）和混合哈密顿量  （探索解空间）制备量子态： 优势：层数  增加时趋近最优解，但传统分析依赖高围长假设（为了保证局部邻域为树结构）。

03

理论结果

针对加法积图  ，本文首次推导期望割分数的闭式迭代公式：

该公式的推导是基于我们研究的图的特殊底层构造。加法积图子图结构类似，利用这一点，我们能够迭代地分析低围长图中的循环，并获得此类低围长图的预期切割分数。

这一理论分析框架不仅适用于标准 QAOA，还被成功推广到了参数更灵活的多角度 QAOA。更进一步，此方法还被扩展用于分析量子最大割问题在加性乘积图上的表现 ，这推广了现有文献中对高围长规则图上量子 MaxCut 问题的研究。

04

数值实验

为了在实际中评估 QAOA 及其变体的性能，并与当前最优的经典方法进行比较，我们进行了一系列数值实验。

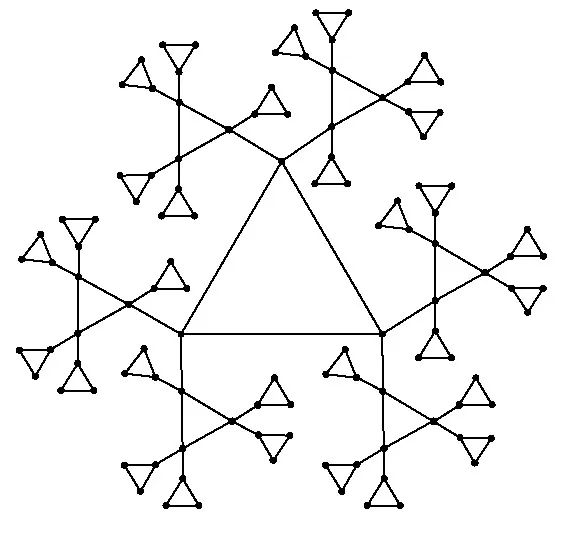
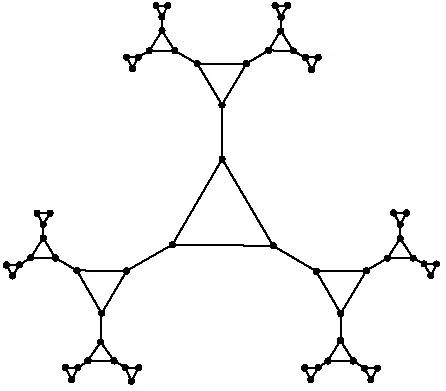
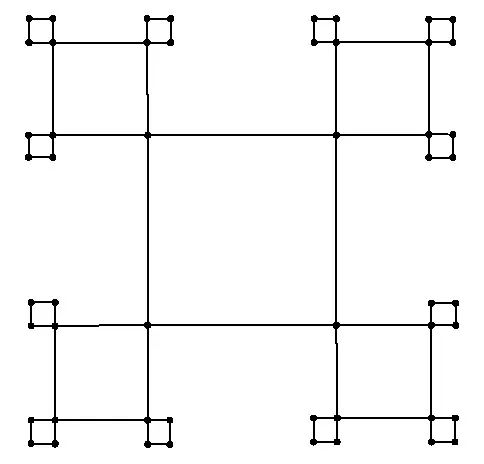
经典基准算法： 我们选取了文献中最优的经典局部算法作为性能比较的基准，主要包括 Barak 和 Marwaha 提出的  -局部算法及其变体，以及阈值算法（threshold algorithm）。

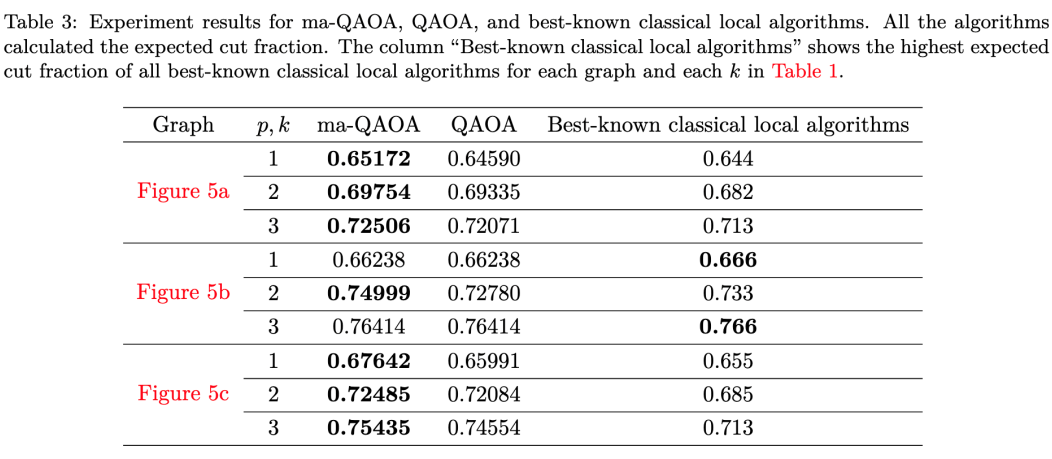
在多种不同参数的加性乘积图上，当算法层数  （对应经典算法的局部性参数 k）为 1, 2, 3 时，标准 QAOA 相较于最优经典局部算法，在预期切割分数上实现了 0.3% 至 5.2% 的提升 ，而 ma-QAOA 通过为图中不同类型的边分配独立的参数，能够更精细地捕捉图结构特征，将 QAOA 的优势进一步提升了 0.6% 至 2.5% 。

特别值得一提的是，在某些图实例中，标准 QAOA 的表现可能略逊于或持平于经典算法，但 ma-QAOA[4]仍能展现出明显优势，超越经典算法。为了验证算法在更广泛图类别上的适用性，我们将实验扩展到了几类具有网格状或密铺结构的平面图上，这类图的扩展方式与加性乘积图的树状分层结构有显著区别 。

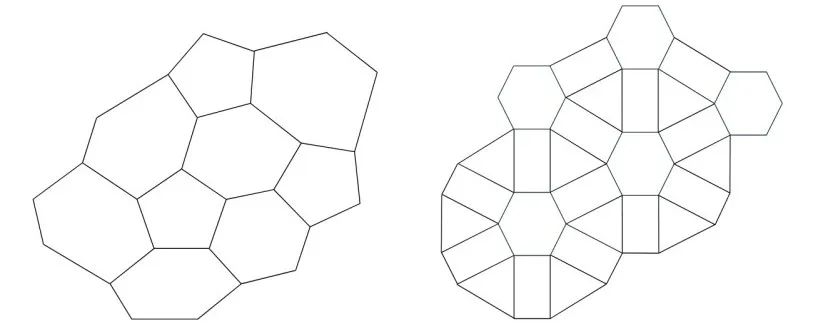
实验结果表明，在这些平面图上（测试了  的情况），QAOA 同样表现出优于经典算法的性能，提升幅度约 0.3% 至 2.2% 。ma-QAOA 也能在 QAOA 的基础上带来约 0.1% 至 0.9% 的额外性能增益 。

05

结论与开放性问题

本研究系统地考察了 QAOA 及其多角度变体 ma-QAOA 在低围长图这一重要图类别上解决最大割问题的性能，并通过严谨的理论分析和充分的数值实验，证明了其相较于当前已知的最优经典局部算法具有一定的优势。

我们的工作引出了若干值得进一步探讨的开放问题：

1）QAOA 在其他类型的低围长扩展图（例如具有不同谱特性或扩展性质的图）上的性能表现如何？图的各种扩展性质（如顶点扩展、边扩展或谱扩展）具体如何影响 QAOA 与经典算法之间的性能差距？

2）如何理解 QAOA 的理论性能界与经典的 Goemans-Williamson 算法为一般图提供的 0.878 近似保证之间的关系？

3）更高层数（  ）QAOA 在低围长图上的潜力？

参考文献

[1] Boaz Barak and Kunal Marwaha, Classical algorithms and quantum limitations for maximum cut on high-girth graphs, ITCS 2022.

[2] Joao Basso, Edward Farhi, Kunal Marwaha, Benjamin Villalonga, and Leo Zhou, The quantum approximate optimization algorithm at high depth for MaxCut on large-girth regular graphs and the SherringtonKirkpatrick model, TQC 2022.

[3] Edward Farhi, Jeffrey Goldstone, and Sam Gutmann, A quantum approximate optimization algorithm, 2014, arXiv:1411.4028.

[4] Rebekah Herrman, Phillip C. Lotshaw, James Ostrowski, Travis S. Humble, and George Siopsis, Multi-angle quantum approximate optimization algorithm, Scientific Reports 12 (2022), no. 1, 6781.

图文 | 杨子熠

PKU QUARK Lab

关于量子算法实验室

量子算法实验室 QUARK Lab (Laboratory for Quantum Algorithms: Theory and Practice) 由李彤阳博士于2021年创立。该实验室专注于研究量子计算机上的算法，主要探讨机器学习、优化、统计学、数论、图论等方向的量子算法及其相对于经典计算的量子加速；也包括近期 NISQ (Noisy, Intermediate-Scale Quantum Computers) 量子计算机上的量子算法。

实验室新闻：#PKU QUARK

实验室公众号：

课题组近期动态

ICLR 2025 | 量子算法求解非凸优化问题的鲁棒性

CMP | 基于朗之万动力学的量子优化算法

Quantum | 量子态的自适应在线学习

Quantum | 低能量子空间中数字量子模拟的复杂度：应用与下界

—   版权声明  —

本微信公众号所有内容，由北京大学前沿计算研究中心微信自身创作、收集的文字、图片和音视频资料，版权属北京大学前沿计算研究中心微信所有；从公开渠道收集、整理及授权转载的文字、图片和音视频资料，版权属原作者。本公众号内容原作者如不愿意在本号刊登内容，请及时通知本号，予以删除。

点击“阅读原文”转论文链接

内容中包含的图片若涉及版权问题，请及时与我们联系删除