本文探讨了如何解读大型语言模型（LLM）生成的推理链（CoT），解决其可解释性难题。研究将CoT分解为句子，提出通过反事实重采样、注意力分析和因果干预等方法，识别影响推理结果的关键句，即“思想锚点”。研究发现，规划和不确定性管理相关的句子通常是关键，而计算相关的句子重要性较低。通过案例分析，验证了这些方法能够帮助理解推理过程，为LLM的可解释性研究提供了新思路和工具。

🧠 通过将推理链（CoT）分解为句子，研究人员找到了一个更易于管理和分析的单位，从而提高了对LLM推理过程的理解。

🔄 研究提出了三种方法来识别CoT中的关键句子：反事实重采样、注意力模式分析和通过注意力抑制进行的因果干预。这些方法帮助定位影响推理结果的关键点。

💡 研究发现，规划和不确定性管理相关的句子往往是CoT中的“思想锚点”，对推理结果有重要影响。而执行实际计算的句子重要性相对较低。

🧪 通过案例研究，研究人员展示了这些方法在分析LLM解决数学问题时的应用，揭示了关键句子如何塑造整个推理过程。

Published on July 2, 2025 8:16 PM GMT

This post is adapted from our recent arXiv paper. Paul Bogdan and Uzay Macar are co-first authors on this work.

TL;DR

Interpretability of chains-of-thought (CoTs) produced by LLMs is challenging:
Standard mechanistic interpretability studies a single token's generation but CoTs are sequences of reasoning steps that use thousands of tokensNeural networks are deterministic but reasoning models are not, because they use sampling
We propose decomposing CoTs into sentences as our unit of analysis
A key step in mechanistic interpretability is decomposing the computation and analyzing the intermediate states and their connections. Sentences are the intermediate states of a reasoning trace, so this is a natural analog
We can do far more than passively read CoTs. We propose three methods for studying important sentences in a CoT: a) counterfactual resampling, b) attention analysis, and c) causal intervention via attention suppressionWe use our methods to identify "thought anchors": critical sentences that guide the rest of the reasoning trace and largely determine the model's final answer
Planning and uncertainty management sentences are consistently identified as thought anchors
We measure sentence importance via resampling
If we fix the reasoning trace up to a specific sentence, this defines a conditional distribution over the rest of the CoT.  A sentence is important if it changes the average accuracyResampling from that point onwards samples from this distributionThe original CoT is just a single sample, we need to resample to approximate it well
We believe interpretability of reasoning models is tractable, but may require very different approaches
To see for yourself how well ours works, check out our interactive tool at thought-anchors.com, and see our paper, code, and CoT resampling dataset

Introduction

Reasoning LLMs have recently achieved state-of-the-art performance across many domains. However, their long-form CoT reasoning creates significant interpretability challenges as each generated token depends on all previous ones, making the underlying computation difficult to decompose and understand.

We present a vision for interpreting CoT by decomposing it into sentences. A sentence-level analysis is more manageable than looking at the token level, as sentences are usually 10-30x less numerous. Additionally, one sentence often puts forth a single proposition, leading us to suspect this is a meaningful logical unit. While future work may yield more sophisticated strategies for dividing CoT into atomic steps, we believe sentences can serve as a reasonable starting point for investigating multi-token computations. 

We find that not all sentences in these reasoning traces are created equal: some are merely computational steps, while others are critical pivot points that determine downstream reasoning and the final outcome. Our research identifies these pivotal moments, which we term thought anchors, and provides methods for finding and examining thought anchors in reasoning traces. Focusing on thought anchors enables targeted examinations of model decisions that guide a reasoning trace.

Identifying Thought Anchors

Method 1: Counterfactual resampling. We measure each sentence's counterfactual importance by resampling the model 100 times, starting from said sentence and contrasting semantically different alternatives. If replacing one sentence dramatically alters the final answer distribution, that sentence is a thought anchor. Compared to prior work interrupting CoTs and requiring the model to answer immediately, our strategy reveals how a sentence may initiate computations leading to a final answer, even if said sentence doesn't perform those computations itself.

Method 2: Attention pattern analysis. We examine how some sentences receive an outsized degree of attention from the downstream reasoning trace. We identify "receiver heads": attention heads that tend to pinpoint and narrow attention to a small set of sentences. These heads reveal sentences receiving disproportionate attention from all future reasoning steps, providing a mechanistic measure of importance.

Method 3: Causal intervention via attention suppression. We examine the causal links between specific pairs of sentences by suppressing all attention to a given sentence and measuring the effect on all subsequent sentences' logits (measured as the KL divergence relative to no suppression). This reveals causal dependencies between sentence pairs, allowing us to map the logical structure of reasoning traces with greater precision than resampling alone.

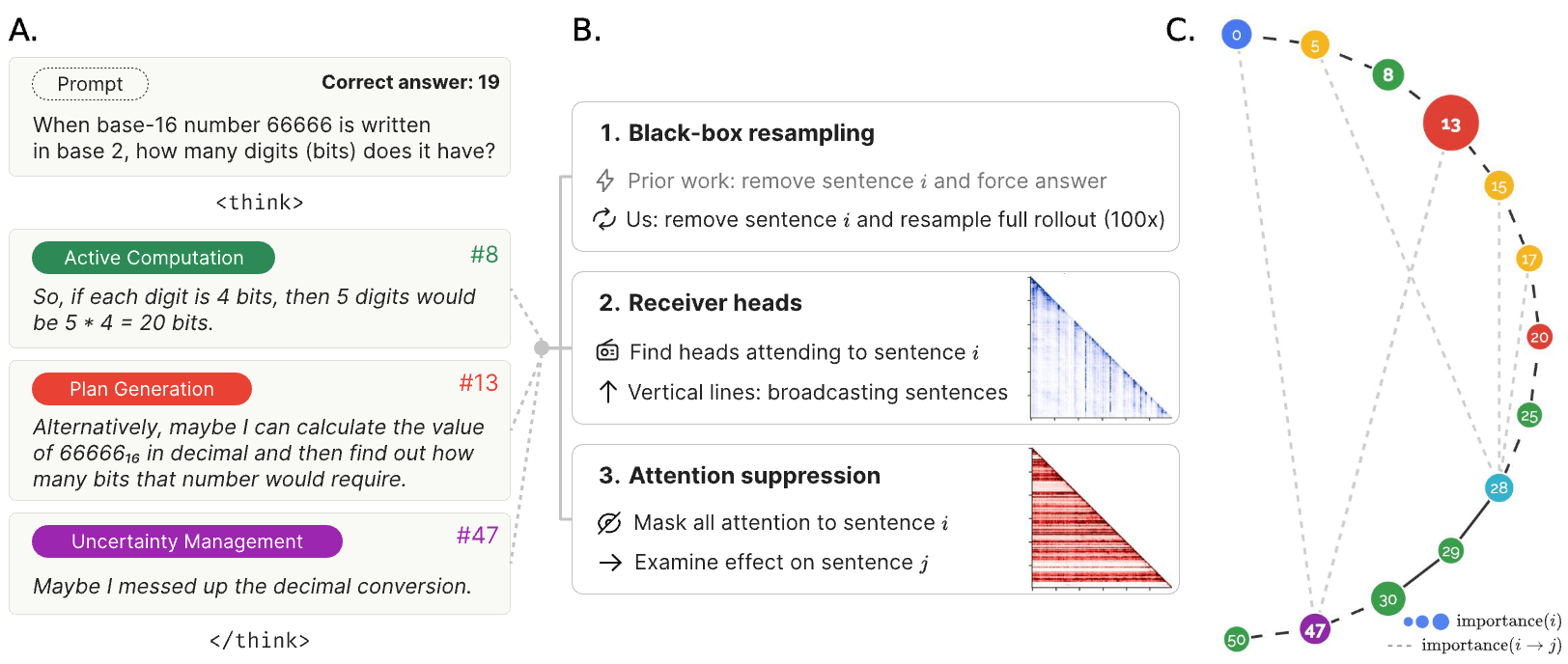
Key Findings

Across all three methods, we find our measures of importance implicate sentences organizing the reasoning process rather than performing computations. These important thought anchors typically fall into two categories:

Planning sentences that establish strategies for solving the problemUncertainty management including confusion, backtracking, and error correction

Meanwhile, active computation sentences (despite being the most numerous) show relatively low importance scores. This suggests that reasoning traces are structured around high-level organizational decisions that determine computational trajectories.

Analyses of receiver heads further show that planning and uncertainty management sentences receive a greater degree of attention from all downstream sentences. 

Case Study: Base-16 Conversion Problem

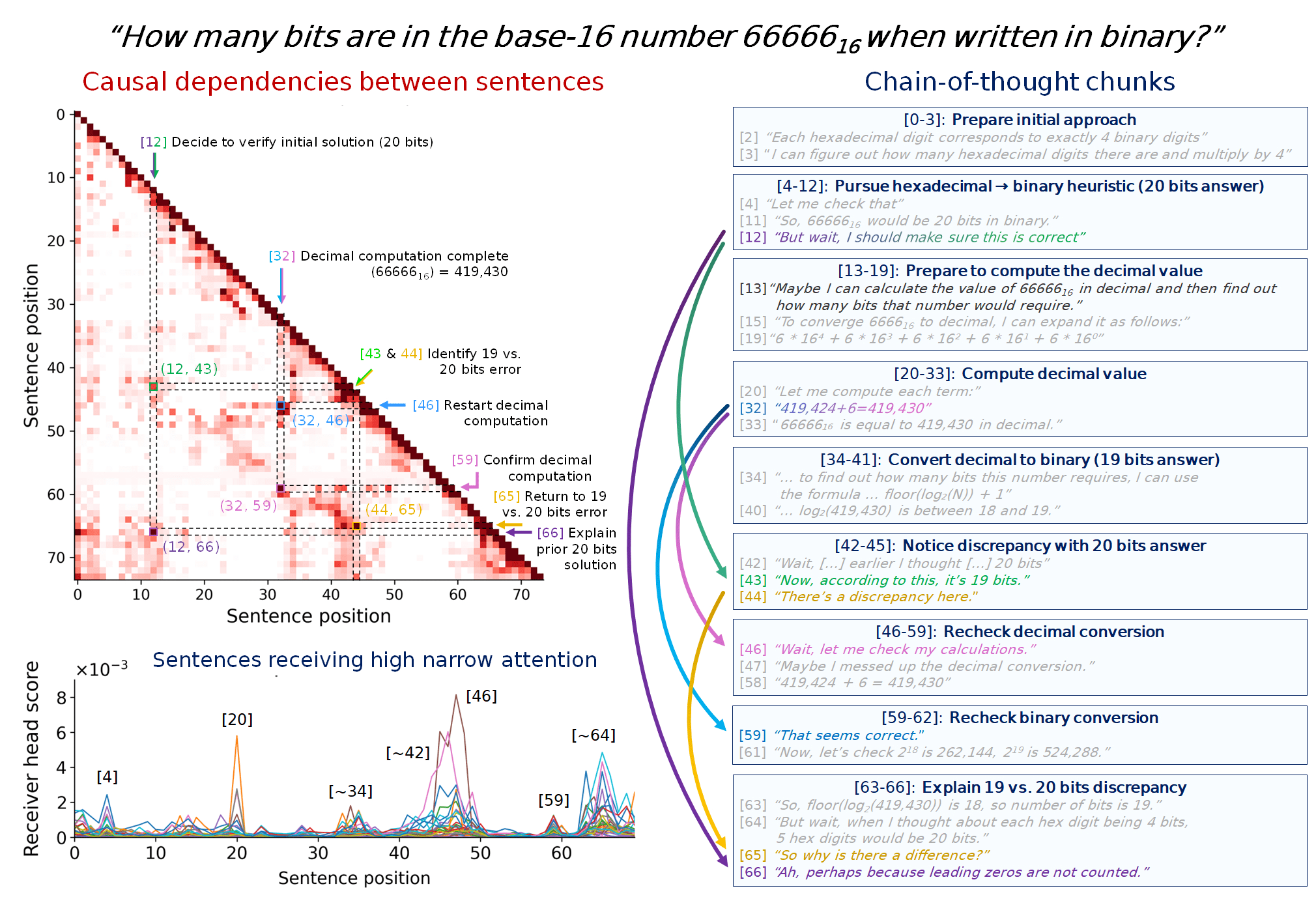
We performed a case study of the CoT used by R1-Qwen-14B to solve this problem: "When base-16 number 66666₁₆ is written in base 2, how many digits does it have?"

The model initially pursues a heuristic approach: 5 hexadecimal digits × 4 bits each = 20 bits. However, this strategy overlooks that 6 in hexadecimal corresponds to 0110 in binary, meaning that there is a leading zero, which should be omitted. At sentence 13, the model pivots toward a solution that would  lead it to making that realization about leading zeroes and ultimately finding the correct answer:

[13] "Alternatively, maybe I can calculate the value of 66666₁₆ in decimal and then find out how many bits that number would require."

Resampling analysis shows that sentence 13 has high counterfactual importance. That is, alternative phrasings at this position typically lead to incorrect final answers. 

On route to the correct answer, receiver head analysis identifies the sentences initiating the necessary computations. For example, sentences 20, 34, 42, 46, 59, and 64 all receive high attention from these specialized heads, segmenting the reasoning process into logical steps like "Compute decimal value" and "Notice discrepancy with 20 bits answer".

Finally, our attention suppression method reveals the causal dependencies between these key sentences, mapping the flow of logic. For instance, it shows a direct causal link from the decision to recheck the initial answer (sentence 12) to the later identification of a discrepancy (sentence 43) and the eventual explanation for the error (sentence 66). Together, these complementary methods illustrate how a few critical thought anchors structure the entire reasoning process.

You can find a more detailed breakdown of this case study in Section 6 of our paper, a video visualization of this case study in our tweet thread, or you can explore the CoT yourself as the "Hex to Binary" problem in our interface.

Implications and Applications

Decomposing chain-of-thought and understanding important steps has several implications:

Understanding faithfulness and deception. CoT faithfulness research (e.g., [1], [2]) often asks why a model does not mention some information in its CoT, given that the information influenced its decision. We suspect it would be informative to instead ask why a model says anything at all in its CoT and, from this direction, clarify why some desired information is omitted. This lens requires understanding the structure of a CoT. We are actively working on applying our approaches for this direction. 

Faster and more principled debugging. When investigating CoT, knowing which sentences have the highest maximum counterfactual impacts encourages focusing on understanding specifically those parts of the CoT. Potentially, this can speed up monitoring at scale if our techniques are used as ground truth to bootstrap more scalable methods. Additionally, simply eyeballing importance based on an intuitive reading of a CoT transcript will often fail to identify the most counterfactually important sentences. For example, in the flow chart above, Sentence 13 has by far the highest importance and all downstream sentences' contents are determined by it.

Mechanistic interpretability. Our work begins to work on mechanistic interpretability specifically focusing on CoT. Reasoning seems poised to play a valuable role in future LLM development, and thus our work seems like a productive extension to the existing mechanistic interpretability literature, which has mostly not considered computations depending on the interactions between many tokens.

Methodology and Tools

We developed our analysis using the DeepSeek R1-Distill Qwen-14B and Llama-8B models on challenging mathematics problems from the MATH dataset. Our sentence taxonomy categorizes reasoning functions into eight types: problem setup, plan generation, fact retrieval, active computation, uncertainty management, result consolidation, self-checking, and final answer emission.

We have released an open-source visualization tool at thought-anchors.com that displays reasoning traces as directed acyclic graphs, with thought anchors represented as prominent nodes and causal dependencies shown as connections between sentences.

Future Directions

This work establishes that reasoning traces possess higher-level structure organized around critical decision points, which can be discovered through interpretability methods. If we can systematically identify thought anchors, we may be able to develop more targeted interventions for steering reasoning processes toward desired outcomes. 

Several important questions remain: How do thought anchor patterns vary across problem domains? Can we predict where pivotal reasoning moments will occur? Could models be trained to explicitly mark their most important reasoning steps? 

We view this as preliminary work. A more detailed discussion of the limitations of our methods can be found in Section 8 of our paper.

Acknowledgments 

This work was conducted as part of the ML Alignment & Theory Scholars (MATS) Program. We would like to thank Iván Arcuschin, Constantin Venhoff, and Samuel Marks for helpful feedback. We particularly thank Stefan Heimersheim for his valuable feedback and suggestions, including ideas for experimental approaches that strengthened our analysis and contributed to the clarity of our presentation. We also thank members of Neel Nanda's MATS stream for engaging brainstorming sessions, thoughtful questions, and ongoing discussions that shaped our approach.

 

Our full paper is available on arXiv: https://arxiv.org/abs/2506.19143.

Code: https://github.com/interp-reasoning/thought-anchors 

Dataset: https://huggingface.co/datasets/uzaymacar/math-rollouts

Discuss