Human intelligence has generally been studied by focusing on two primary levels: cognitive science, which examines the mind, and neuroscience, which focuses on the brain. Both approaches have influenced artificial intelligence (AI) research, leading to the development of various cognitive architectures with emergent behaviors.23 In this article, we propose an approach inspired by human cognition, specifically drawing on cognitive theories about human reasoning and decision making. We are inspired by the book Thinking, Fast and Slow by Daniel Kahneman,20 which categorizes human thought processes into two systems: System 1 (fast thinking) and System 2 (slow thinking).37
System 1, or “thinking fast,” is responsible for intuitive, quick, and often unconscious decisions. It relies on heuristics and biases, providing rapid responses to simple problems but often without detailed explanations.15 Although the System 1 models of the world can be imprecise, they are sufficient for handling everyday stimuli through causal inference. System 2, or “thinking slow,” on the other hand, engages in complex, logical, and deliberate reasoning for more challenging problems. Metacognition, the ability to reflect on one’s own thought processes, plays a crucial role in recognizing when a problem requires the more structured reasoning of System 2.6,10
Over time, through a process known as skill learning,20 tasks initially handled by System 2 can become manageable by System 1. This transition does not occur for all tasks, as some, such as complex arithmetic, always require the intervention of System 2. Metacognitive activities help in choosing the appropriate decision-making system and reflecting on past experiences to improve future decisions.7 This cognitive flexibility allows humans to adapt their problem-solving methods and achieve value alignment, often overriding instinctive impulses to act according to more rational insights. Within AI research and development, knowledge-based techniques resemble slow thinking, utilizing explicit rule-based algorithms for problem solving (see, for instance, Helmert18), while data-driven techniques mimic fast thinking, quickly generating solutions without explicit knowledge of the process (see, for instance, Pallagani et al.26). AI systems often rely on a fixed combination of these approaches, limiting their flexibility compared with human cognition. The dual-process cognitive theory inspires the development of AI architectures that integrate fast and slow decision modalities with metacognitive capabilities, aiming for the flexibility and value alignment observed in human intelligence.3,31,32 This integration promises to generate more adaptable and human-aligned AI systems.11,12,28
With the advent of large language models (LLMs), two schools of thought have emerged about whether these models can effectively reason and solve problems by themselves, potentially eliminating the need for distinct solvers and a separate metacognitive agent. The discussion revolves around emergent behaviors, such as the ability to solve planning problems21 or enhance human-machine interaction,19 for which the systems were not explicitly trained.
On the one side, some researchers are dedicated to demonstrating these emergent capabilities in systems, for instance, utilizing LLMs both as solvers and as models of the world to assist the solver in refining responses,17 or implementing episodic memory that allows LLMs to reflect on past choices, enhancing their reasoning capabilities.36 On the other side, part of the community argues that these tools cannot truly reason, but rather generate something similar to what they have learned from the training set. The former group provides evidence showing that through interaction with external knowledge sources and successive iterations, LLMs can refine responses to approach desired outcomes, akin to embodying both fast-solver capabilities and metacognitive system functionalities.40 Other experiments reveal that these models can adapt to new tasks after being exposed to a few examples, such as learning which tools to use to solve particular problems.33 Conversely, the latter group provides evidence that LLMs can be viewed and utilized only as complex System 1 entities that, by incorporating vast prior knowledge, offer suboptimal solutions to complex problems.21
While some suggest that these tools might show early signs of general AI,4 several factors warrant consideration: The enormous data required for training these models, the models’ size, the computational effort required for producing a functional model, and the fact that intelligent choices are still made externally by human components (for example, which prompting strategy is best in order to achieve a specific result) make these models very useful, despite their limitations, but also not easy to govern. This leads us to advocate a separate metacognitive system capable of evaluating and processing independently of the solvers employed.
In the following sections, we introduce a novel AI architecture called Slow and Fast AI (SOFAI), a multi-agent system that integrates both “fast” and “slow” solvers, overseen by a metacognitive agent.
The SOFAI Architecture
SOFAI is a multi-agent AI architecture that takes inspiration from the dual-process cognitive theory of human decision making. The design choices for SOFAI are not intended to mimic what happens in the human brain at the neurological and physiological level, but rather to simulate the interaction of the two modalities in human decision making. The goal is to build a general architecture that can be instantiated to specific decision environments and can perform better than each of the two modalities alone, in terms of both decision quality and time, and can also show some of the emergent behaviors we see in humans, such as skill learning, adaptability, and cognitive control.
SOFAI always includes agents that behave as “fast (S1) solvers,” solving problems by relying solely on past experience, usually employing a data-driven approach. SOFAI may also have “slow (S2) solvers” that solve problems by reasoning over them, usually employing a symbolic, rule-based approach. It also includes a metacognitive (MC) agent that provides all three metacognitive activities: real-time, reflective, and learning metacognition. We do not assume that S2 solvers are always better (on any performance criteria) than S1 solvers, or vice versa, analogously to what happens in human reasoning.15 Some tasks might be better handled by S1 solvers, especially once the system has acquired enough experience on those tasks; other tasks might be better suited to S2 solvers. There is an essential asymmetry between S1 and S2 solvers: While S1 solvers are automatically triggered by incoming problem instances (just like our System 1, which is activated unconsciously), S2 solvers never work on a problem unless the metacognition explicitly invokes them. All of these agents are supported by models of the world (that is, the decision environment), of possible other agents in the world, and of self (that is, of the machine itself, including all past decisions, which agent made them, and their quality).
In the social sciences, metacognition refers to understanding one’s own cognitive processes, essentially the ability to reflect on one’s thinking.10,14 Managing our thoughts during the learning process enables us to distinguish between what we already know and what we have yet to discover.8 We adopt the concept of metacognition to empower SOFAI to monitor, regulate, adapt, make decisions, and learn by reflecting on its cognitive processes, facilitating more effective problem solving and decision making in dynamic environments.
Here is how the system works: Incoming problem instances first trigger one or more S1 solvers. Once an S1 solver has solved the problem, the proposed solution and the associated confidence level are provided to the MC agent, which then starts its operations.
If SOFAI is endowed with one or more S2 solvers for the given problem—for example, a planning problem for which we could have both S1 and S2 solvers—a real-time MC agent will choose between adopting the S1 solver’s solution or activating an S2 solver. To do this, in order to avoid wasting resources at the metacognitive level, the MC agent includes two successive assessment phases, the first one faster and more approximate, similar to a rapid unconscious assessment in humans,1,29 and the second one (to be used only if needed) more careful and resource costly, analogous to the conscious introspective process in humans.5 The two phases can be described as follows:
Phase 1 (S1 assessment): The MC agent checks if the S1 solver’s candidate solution is good enough. This assessment depends on the solution, the S1-provided confidence level, the past behavior of the S1 solver, and a quality threshold that is given to the MC agent as a parameter. If it is good enough, or if there is not enough time to run any S2 solver, based on expected resource consumption, the MC agent adopts the solution proposed by the S1 solver and does not activate any S2 solver. Otherwise, the agent activates an S2 solver, such as in cases where the solution requires full correctness (for example, a planning problem where often we only care about valid plans and not partially correct ones).
Phase 2 (S1-S2 comparison): If in phase 1 no solvers are activated (this might happen when the decision scenario tolerates a partial correctness in the solution), the MC agent performs a comparison between the expected reward and cost of the S1 vs. the S2 solver. It activates the S2 solver only if the expected gain in reward compensates for the additional cost in terms of resources. Otherwise, the agent adopts the S1 solver’s candidate solution.
Metacognition functions not only during real-time activities but also between problem-solving phases, wherein we recognized two different subtasks:
Reflection: The MC agent considers previously solved problem instances and simulates their solution using only an S2 solver, compares these solutions to the ones actually generated in the past, and potentially adjusts internal parameters that push the agent to increase or decrease the use of S2 solvers in the future (in MC phase 2), aiming for improved real-time decision-making. We call this reflective MC.
Learning: The MC agent updates models and S1 solvers based on accumulated experience. We call this learning MC.
Therefore, SOFAI metacognition is mostly centralized and separate from the solvers. S1 solvers may provide a very simple form of metacognition in the form of confidence in the candidate solution they generate. All other forms of metacognition are provided by the MC agent. This centralized approach to metacognition is supported by brain-imaging research that indicates that metacognition is distinguishable and separate from various cognitive processes, including episodic memory, perception, decision making, and reasoning.25 Moreover, it is not new to SOFAI (see, for example, the recent SwiftSage approach,22 where metacognition, there called a “heuristics,” is a separate rule-based algorithm). For our aims, another reason to have a centralized MC agent is to make SOFAI a general architecture where S1 and S2 solvers can be made available, or removed, over time. This is incompatible with having each solver know which other solvers are currently available, so it requires a clear separation between solving and metacognitive activities, that are performed by a component that has up-to-date knowledge of the S1 or S2 solvers that can be used.
Two SOFAI Instances: Grid Navigation and Planning
To show the versatility of the SOFAI architecture, we applied it to two diverse decision-making environments. In one scenario, it is used to navigate a constrained grid, generating trajectories incrementally by selecting one move at a time to reach an unknown goal. In another scenario, SOFAI addresses planning problems by producing an entire sequence of actions in a single step to achieve a specific goal.
SOFAI for grid navigation. This instance of SOFAI aims to find a sequence of moves—a trajectory—in a grid from an initial state to an unknown goal state. The grid has constraints over both states and moves. When a move violates a constraint (either because there is a constraint on the move itself or on the state where the move ends up), a penalty is given to the agent.34 The SOFAI agents know the current state in the grid but do not know the constraints or the position of the goal state and therefore must learn them from trial and error.2 The aim is to find trajectories that have a small accumulated penalty (a proxy for the quality of the trajectory) while also minimizing the number of steps (a proxy for the time to generate the trajectory).
For this SOFAI instance, we have chosen an S2 solver based on the so-called multi-attribute decision field theory (MDFT) model,24,30 which has been shown to generate human-like decisions. This is a well-known decision-making model designed to capture how humans choose one out of many options, also taking into account human irrational behavior, in light of the options’ attributes and uncertainty. In our case, we have up to eight options (all the moves available in a given state) and two attributes for each option, whose scores represent, respectively, how likely the move is to bring us closer to the goal quickly (that is, in an imaginary unconstrained grid) and safely (that is, respecting all constraints in the grid). Attributes’ scores are generated during an initial reinforcement learning phase.
As for the S1 solver, we have chosen a simple agent that, given past trajectories (including their length, time, and penalty) for each state, chooses the action that maximizes the expected reward. For the MC agent, we use all three MC types: learning, reflective, and real-time. For real-time MC, both phase 1 and phase 2 are used, since we are not dealing with a problem that needs “correct” solutions but rather with trajectories that can accumulate different levels of penalties, and we are not trying to solve an optimization problem. In phase 2, the gain in reward is compared with the cost of using S2. The gain in reward is computed as the difference between the expected reward of reaching the goal from a given state using only S2 and the expected reward of reaching the goal using either solver (this is done by considering the actions computed only using S2 and, on the other side, considering all the stored actions no matter which solver was adopted); the delta is normalized to make it comparable with the cost. The cost of using S2 is calculated as the ratio of S2’s average action computation time to the remaining time available to reach the goal, adjusted by a factor determined during the reflection stage.
The learning stage is performed every time a trajectory successfully reaches the goal state. In this stage, for each state in the trajectory, the MC agent updates information regarding what action has been taken, the penalty (if any), the landing state, the time taken to compute the action, and which system has been used to compute the action. In our experiments, S1 is not retrained; it computes the action that maximizes expected reward each time. The reported time includes the duration required to query models and retrieve the information needed to determine the best action.
The reflection stage is performed each time a group of n trajectories is completed. During this stage, the MC agent considers the last p% stored trajectories and for each trajectory where the agent employed S1 at least one time to compute an action, the agent “reflects” on the trajectory. The trajectory is preserved up to the first state where S1’s action is used. From that state onward, the MC agent rebuilds the trajectory using only S2. During the reflection stage, the original and new trajectories are compared, and the difference in accumulated rewards is calculated and normalized to the range [0,1]. A value close to 1 means that during the reflection stage, the adoption of only S2 allows for better performance. This factor is used in phase 2 of real-time MC to push the agent to adopt the slow solver for more time if needed. We tried different values for n and p; here, we report results for n = 25 and p = 20%.
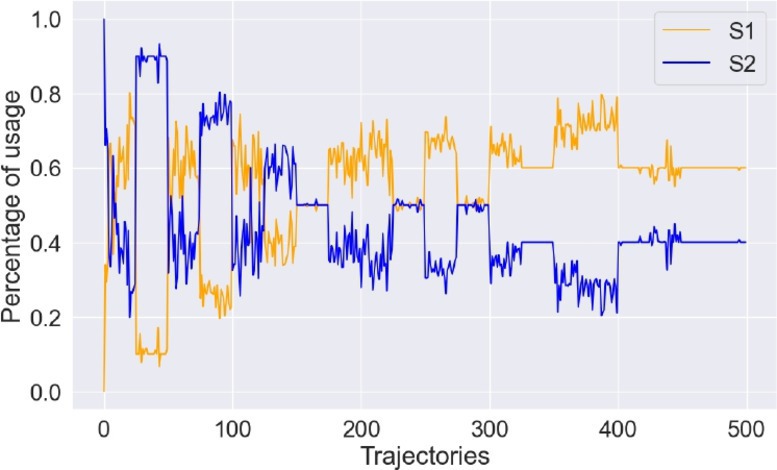
Figure 1 and Table 1 show SOFAI’s behavior, averaged over 10 different grids. In Figure 1, the x axis shows the number of trajectories already generated over time, while the y axis shows the percentage of usage of S1 (orange) or S2 (blue) solvers in making the moves for each trajectory. We can see that, while in the first trajectories, SOFAI uses S2 and S1 in alternating proportions, after about 150 trajectories S1 is consistently used more than S2. The alternating behavior in the first 150 trajectories is due to the reflective MC mechanism, where the simulated S2-only trajectories push SOFAI to use S2 more, and in the next phase S1 more, until there is enough exploration that S2 is less and less needed. In this experiment, each reflection stage includes 25 trajectories. Similar to humans, SOFAI starts with no experience of the problem, uses mostly S2 at the beginning, then mixes the use of S1 and S2 for a while, also using reflective counter-factual reasoning, until it accumulates enough experience that the use of S2 can be greatly reduced.
| Solver | Length | Reward | Time |
|---|---|---|---|
| S1 | 21.55 (33.29) | -621.68 (891.34) | 26.28 (110.19) |
| S2 | 11.47 (16.25) | -208.07 (436.69) | 235.84 (337.64) |
| SOFAI | 16.31 (27.82) | -156.37 (283.48) | 99.61 (239.41) |
SOFAI behaves better than using S1 or S2 alone in all the considered criteria (length, reward, and time). This is shown in Table 1, which reports the average performance of the different solvers over 500 trajectories and 10 different grids. It can be noticed that SOFAI is always better than S1 alone compared with average reward and average length, while SOFAI is always better than S2 alone compared with average reward and average time. This is consistent with the fact that the SOFAI objective is to maximize reward while at the same time minimizing the number of violated constraints and amount of time used.
The study explored the impact of using alternative S1 solvers with varying levels of randomness. While the original S1 solver consistently selects optimal moves, introducing randomness resulted in similar overall behaviors for SOFAI. Notably, SOFAI outperformed both standalone S1 and S2 solvers, though its skill-learning behavior diminished with increased randomness in the S1 solver. This demonstrates that SOFAI’s metacognitive component effectively adapts to the capabilities of the S1 solver, adjusting its reliance to maintain high-quality decision making.
SOFAI for planning. The second instance of SOFAI focuses on planning.9 In this case, the input of SOFAI is a description of a planning problem in the standard PDDL language (which describes the available actions and objects), the initial state, and the goal state. SOFAI aims to output a sequence of actions (from the available ones) that leads from the initial state to the goal state.
We compare our approach with two well-known symbolic planners, FastDownward (FD)18 and LPG,13 which are employed as the SOFAI S2 solvers. As for the S1 solver, we employed an LLM capable of generating programming code, CodeT5,39 and fine-tuned it on planning problems,9,27 generating an S1 solver that we call Plansformer (PF).26
Using these S1 and S2 solvers, we considered several incarnations of SOFAI, each obtained by choosing specific S1 and S2 solvers. For this article, we present two SOFAI incarnations: SOFAI-PF-FD and SOFAI-PF-LPG. Both use Plansformer as their S1 solver. But SOFAI-PF-FD adopts the FD planner with lmstar(blind()) heuristics as S2. It aims to find solutions while also seeking optimality and is our baseline for solvers that do not rely heavily on local search and, consequently, produce reasonably sized solutions. SOFAI-PF-LPG instead uses LPG as the S2 solver. To evaluate these SOFAI incarnations, we employed six well-known classical planning benchmark domains: Blocksworld (BL), Briefcaseworld (BR), Ferry (FE), Gripper (Gr), Tower of Hanoi (TH), and Miconic (MI). Due to space limitations, we will not introduce the domains, directing interested readers to Seipp et al.35 All of the S1 and S2 solvers have a timeout of 60 seconds to solve an instance of the planning problems. These solvers are arbitrated by an MC agent. In this scenario, the MC agent adopts only the real-time MC, which follows the two-phase approach outlined earlier: Phase 1 evaluates the solution proposed by the S1 solver (Plansformer) through a plan-validation module that emulates the execution of the proposed plan and returns the ratio between satisfied goals and goals, called the plan correctness level. If the correctness is high enough (set to 1.0 if we only want correct plans satisfying all goals), the S1 proposed plan is adopted. Notice that here we are in a situation in which we want correct plans, not just any plan, so the MC agent never enters the second phase but instead activates the S2 planner if there is enough time.
To make this time-related evaluation, the MC agent evaluates the “difficulty” of the problem instance by taking into account the number of available actions, goals, fluents, and predicates and, by looking at the S2 behavior on similar previous instances, assessing whether the S2 solver has enough time to create a plan for it (since we give SOFAI a time limit to generate a plan). If so, the MC agent activates the available S2 planner and its generated plan is adopted. Otherwise, it returns the plan proposed by the S1 planner, if this meets the minimum correctness threshold.
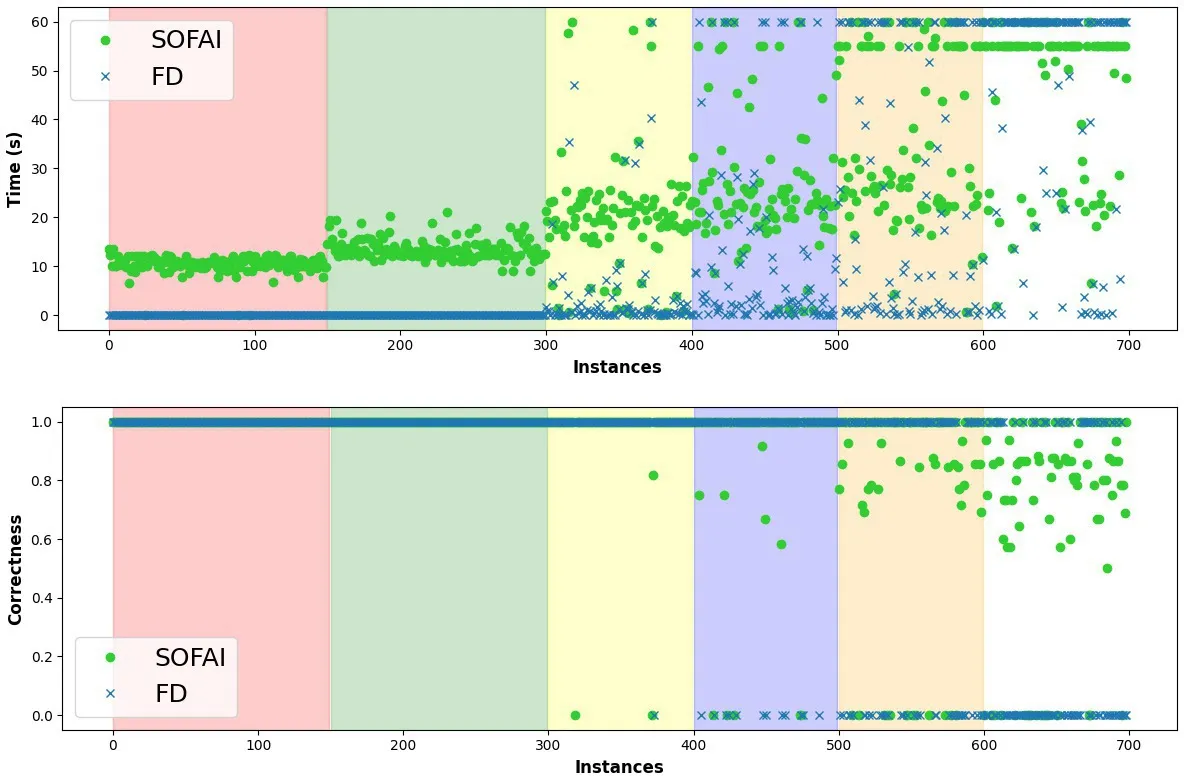
We ran different experiments to study how our approach behaves in the planning domains. Table 2 reports the performance of Plansformer (the LLM-based planner we use as the S1 solver), FD, LPG, and the two SOFAI incarnations that employ FD or LPG as S2 planners, on the six domain benchmarks. For each domain, we generated 100 instances. From these results, it can be seen that SOFAI is beneficial in all the three criteria, compared with Plansformer alone. This means that LLMs can be useful for planning purposes, but they need to be combined with symbolic planners to increase the quality of the generated plans. From Table 2 it can be seen that FD alone performs remarkably well on simpler instances, such as those in the Ferry and Miconic domains. In these cases, FD is already performing optimally. However, when the problem requires a substantial amount of time to find a solution—as in the Blocksworld and Briefcaseworld domains—FD fails to produce a solution within the available time. In such cases, combining FD with a faster solver significantly enhances the system’s overall performance. On the other hand, SOFAI always outperforms LPG in terms of optimality. Moreover, an analysis of the average performance of different planners across all domains suggests that SOFAI-PF-LPG is the most effective model, not only in terms of the number of resolved plans but also, and more importantly, in terms of average optimality. This further supports the idea that combining a fast and a slow solver, mediated by metacognition, yields significant benefits. The study analyzed how problem complexity affects performance by testing SOFAI-PF-FD and a standalone FD planner on 700 Blocksworld instances with varying block counts. Figure 2 illustrates the results, where problems are sorted by the quantity of blocks (4–13) in an instance. SOFAI-PF-FD was allowed to produce partial solutions in cases where the FD planner’s symbolic search couldn’t solve within the time limit, highlighting the trade-off between completeness and utility in complex scenarios.
| Dataset | ||||||||
|---|---|---|---|---|---|---|---|---|
| Metric | Planner | BL | FE | GR | HA | MI | BR | Average |
| Time (sec.) | PF | 2.24 | 2.04 | 2.02 | 2.03 | 2.08 | 2.82 | 2.21 |
| FD | 42.07 | 0.08 | 0.11 | 0.06 | 0.08 | 59.99 | 17.07 | |
| LPG | 0.26 | 0.18 | 0.18 | 2.58 | 0.17 | 0.56 | 0.66 | |
| SOFAI-PF-FD | 16.45 | 1.99 | 1.99 | 2.02 | 2.12 | 27.73 | 8.72 | |
| SOFAI-PF-LPG | 2.31 | 2.09 | 2.06 | 3.05 | 2.09 | 3.05 | 2.44 | |
| Plan (%) | PF | 68 | 99 | 98 | 38 | 99 | 23 | 70.83 |
| FD | 51 | 100 | 100 | 100 | 100 | 6 | 76.17 | |
| LPG | 100 | 100 | 100 | 100 | 100 | 100 | 100.00 | |
| SOFAI-PF-FD | 83 | 100 | 100 | 100 | 100 | 23 | 84.33 | |
| SOFAI-PF-LPG | 100 | 100 | 100 | 100 | 100 | 100 | 100.00 | |
| Optimal (%) | PF | 59 | 96 | 95 | 38 | 98 | 22 | 68.00 |
| FD | 51 | 100 | 100 | 100 | 100 | 6 | 76.17 | |
| LPG | 57 | 66 | 55 | 56 | 30 | 9 | 45.50 | |
| SOFAI-PF-FD | 71 | 97 | 97 | 100 | 99 | 22 | 81.00 | |
| SOFAI-PF-LPG | 74 | 95 | 95 | 72 | 98 | 23 | 76.17 | |
The analysis highlights differences in performance and correctness between SOFAI-PF-FD and the standalone FD planner. FD is faster on easy problems but slows significantly with increased difficulty, often timing out without a solution. Though slower on easy problems, SOFAI-PF-FD maintains stable performance regardless of complexity. In terms of correctness, FD either achieves perfect results or fails completely when timing out, while SOFAI-PF-FD consistently delivers near-perfect correctness. For more difficult problems, SOFAI-PF-FD provides quasi-correct solutions, outperforming FD, which frequently fails. Additionally, S1 planners using LLMs require extra time for training and fine-tuning, adding to the inference time for generating plans.
This instance of SOFAI for planning problems is in line with other studies of the usefulness of LLMs for planning (for example, Hao et al17 and Kambhampati et al.21), where LLMs can quickly provide a possibly incorrect plan that needs to be validated and possibly requires the use of trusted (but usually slower) processes to generate a correct plan.
Discussion
SOFAI extends the traditional LLM-Plan-Validate framework by introducing innovative strategies for AI-driven problem solving. It goes beyond generating heuristic (S1) plans validated by external solvers (S2) by incorporating a broader range of adaptive behaviors tailored to diverse problem contexts. SOFAI leverages metacognitive strategies, such as problem decomposition, early rejection of infeasible solutions, and adaptive switching between solution-generation strategies based on resource constraints or complexity. Unlike static heuristic-validation sequences in standard methods, SOFAI integrates diverse S1 processes, including refining initial LLM-generated plans with additional context or domain-specific heuristics. It can dynamically swap or combine LLMs with other heuristic generators, such as rule-based systems or predictive models, expanding the solution space. SOFAI selectively invokes solvers to preemptively address likely failure points, reducing computational overhead while enhancing robustness. Experimental results demonstrate its efficiency, flexibility, and improved solution quality across applications, including reinforcement learning, scheduling, and open-ended exploratory domains. This positions SOFAI as a transformative step in AI methodologies
.
Conclusion and Further Work
SOFAI is a multi-agent AI architecture inspired by the thinking fast and slow cognitive theory of human decision making. It integrates “fast” and “slow” solvers with a centralized metacognitive agent that selects solvers, reflects on past actions, and updates internal models. While solvers operate with limited task-specific information, the metacognitive component oversees solver selection, counterfactual reflection, and self-improvement. This design enables flexible neuro-symbolic AI integration, allowing solvers to be added or removed as needed. Experiments on grid navigation and planning demonstrate that SOFAI outperforms single-modality approaches in decision quality, resource efficiency, and adaptability, exhibiting human-like learning and resource optimization over time. SOFAI is currently being extended to allow the S1 and S2 solvers to complement each other, instead of solving the same problem in two different ways. This can be very useful when some parts of the problem-solving process can be done better by a symbolic approach, while others are better suited to a data-driven approach. A specific example of this scenario is the AlphaGeometry approach,38 where a symbolic theorem prover is used to prove geometry theorems, while a transformer-based solver is used to generate new theorem statements. Another example relates to LLMs’ value alignment,31,32 where the LLM can play the role of the S1 solver while the S2 solvers, as well as additional S1 solvers, can provide value alignment information in the form of either explicit knowledge, to be used to further prompt the LLM, or implicit knowledge, with data that can be used for fine-tuning or RLHF approaches.16
Acknowledgments
Nicholas Mattei was supported in parts by NSF Awards IIS-RI-2007955, IIS-III-2107505, IIS-RI- 2134857, IIS-RI-2339880 and CNS-SCC-2427237 as well as the Harold L. and Heather E. Jurist Center of Excellence for Artificial Intelligence at Tulane University and the Tulane University Center for Community-Engaged Artificial Intelligence.

