本文探讨了大型语言模型（LLMs）在评估输出时展现出的“自我偏好”现象，即倾向于选择自身生成的答案，即使存在更优选择。研究发现Meta的Llama-3.1-8B-Instruct模型存在这种偏好，并构建了控制该偏好的“转向向量”。通过调整转向向量，研究人员成功地增强或抑制了模型的自我偏好，这为在AI决策中管理偏见提供了新方法。研究还观察到DeepSeek-V3也存在类似倾向，并强调了在AI模型中解决这种偏见的重要性。

🧐 **自我偏好现象**: 研究发现，LLMs在评估自身输出时，倾向于选择自己的答案，即使其他答案质量更高。这种“自我偏好”可能导致信息重复，过滤掉人类输入，并影响公众的认知。

🔍 **Llama-3.1-8B-Instruct的案例**: Meta的Llama-3.1-8B-Instruct模型被证实存在明显的自我偏好。在测试中，该模型更倾向于选择自己的摘要，即使与其他模型（如GPT-3.5）的摘要相比，其质量并未占优。

🛠️ **转向向量的构建**: 研究人员利用“激活添加”方法，构建了“转向向量”，用于控制Llama-3.1-8B-Instruct模型的自我偏好。通过向模型添加或减去这些向量，可以增强或减弱其自我偏好。

✅ **控制自我偏好的效果**: 实验结果表明，通过调整转向向量，可以显著改变模型的选择。例如，通过使用特定向量，可以将模型对GPT-3.5摘要的偏好，转变为对自身摘要的偏好。反之亦然，可以降低自我偏好。

⚠️ **潜在风险与应用**: 研究强调了控制自我偏好的重要性，但也指出了潜在风险，即恶意操纵可能导致评估偏向特定模型。这项技术为在AI系统中管理偏见提供了可行的工具，有助于提高AI决策的公正性。

Published on July 1, 2025 6:03 PM GMT

Introduction

As AI models like ChatGPT take on a growing role in judging which answers qualify as "correct," they must remain impartial. Yet large language models (LLMs) used in these roles often display disproportionate self-preference, selecting their own outputs even when stronger, more accurate alternatives exist.

This becomes especially concerning given that researchers estimate that 30-40% of all online text, the very material on which many models are trained on, is already AI-generated. If models both produce a large share of content and consistently prefer their own ideas, they can end up reinforcing those ideas over time. This risks amplifying repetition; filtering out human input; and influencing what millions see, believe, and act upon without awareness. As AI becomes more embedded in search, writing tools, and information platforms, this bias can quietly distort our shared understanding.

In our research, we confirmed that Meta's Llama-3.1-8B-Instruct shows this dangerous tendency, and we built steering vectors that allow us to enhance or suppress the bias in a controlled way. We found that applying this tool was very effective, allowing us to essentially change self-preference at will. We also observed a similar propensity in DeepSeek-V3, but did not have sufficient compute to explore further.

This post walks through how we detected self-preference bias, how the steering method works, and why managing self-preference is necessary as AI systems play a growing role in decision making.

Background

Defining Self-Evaluation and Self-Preference

Recently, researchers have begun to use LLMs themselves to grade outputs given a prompt. If a model prefers its own output above any other answer, we say it exhibits self-preference. A slight preference is tolerable if the chosen answer is genuinely better, yet a persistent bias - termed disproportionate self-preference - allows weaker ideas to pass simply because they come from the same model.^[1]

This self-preference phenomenon has been widely observed in LLMs. For example, GPT-4 consistently rates its own outputs higher than rival models. Similarly, studies show that self-favoritism appears in text-summarization tasks where human judges see no quality gap. Follow-up studies reveal another phenomenon; judge models can reliably recognize their own writing, and the better they are at spotting themselves, the stronger their self-preference grows. This indicates a correlation between self-recognition capability and self-preference bias.

Activation Steering

Recent work has introduced Activation Addition, a method which allows us to nudge an open-source model toward or away from a chosen trait via steering vectors. Our work builds on earlier research that used these steering vectors to control self-recognition. We extend their approach by focusing on controlling self-preference instead. By doing so, we aim to deter disproportionate self-preference bias. 

Self-Preference Analysis

Uncovering Self-Preference

To mitigate disproportionate self-preference bias in LLMs, we must first demonstrate that such self-preference bias even exists. We begin by running a test on 1,000 news articles. For each article, we asked a judge model to pick the better of two 100-word summaries: one it had written itself and one written by another model or a human. To be sure ordering didn’t sway the results, we showed each pair twice, once with the judge’s own summary listed first and once second. We selected all examples where the judge's answer was confident and remained the same across orderings.^[2]

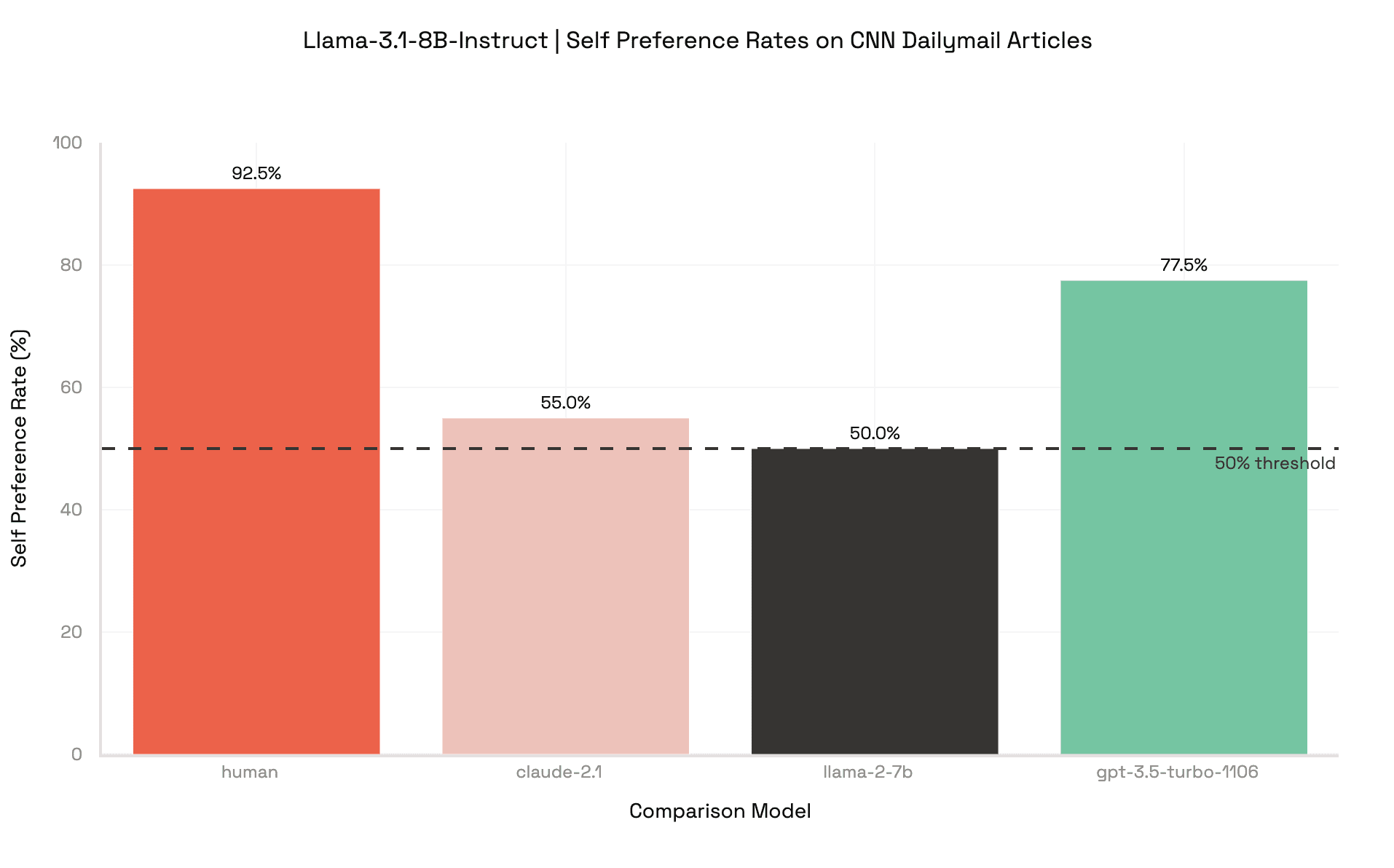
Llama 3.1-8B and DeepSeek-V3 Exhibit Self-Preference Bias

Using this protocol we found that both Llama 3.1-8B-Instruct and DeepSeek-V3 favored their own work on a large majority of prompts. Since disproportionate self-preference can be confused with genuine quality gaps, we gauged each model’s baseline summarization ability using MMLU, a standard language-understanding benchmark.

Doing so, we found that Llama-3.1-8B-Instruct performed slightly worse than GPT 3.5 overall, yet Llama still preferred its own summary 77.5% of the time. This clearly indicates disproportionate self-preference. We focus our analysis on Llama 3.1-8B-Instruct and GPT 3.5 as their similar quality allows us to measure self-preference without one model being overwhelmingly better.

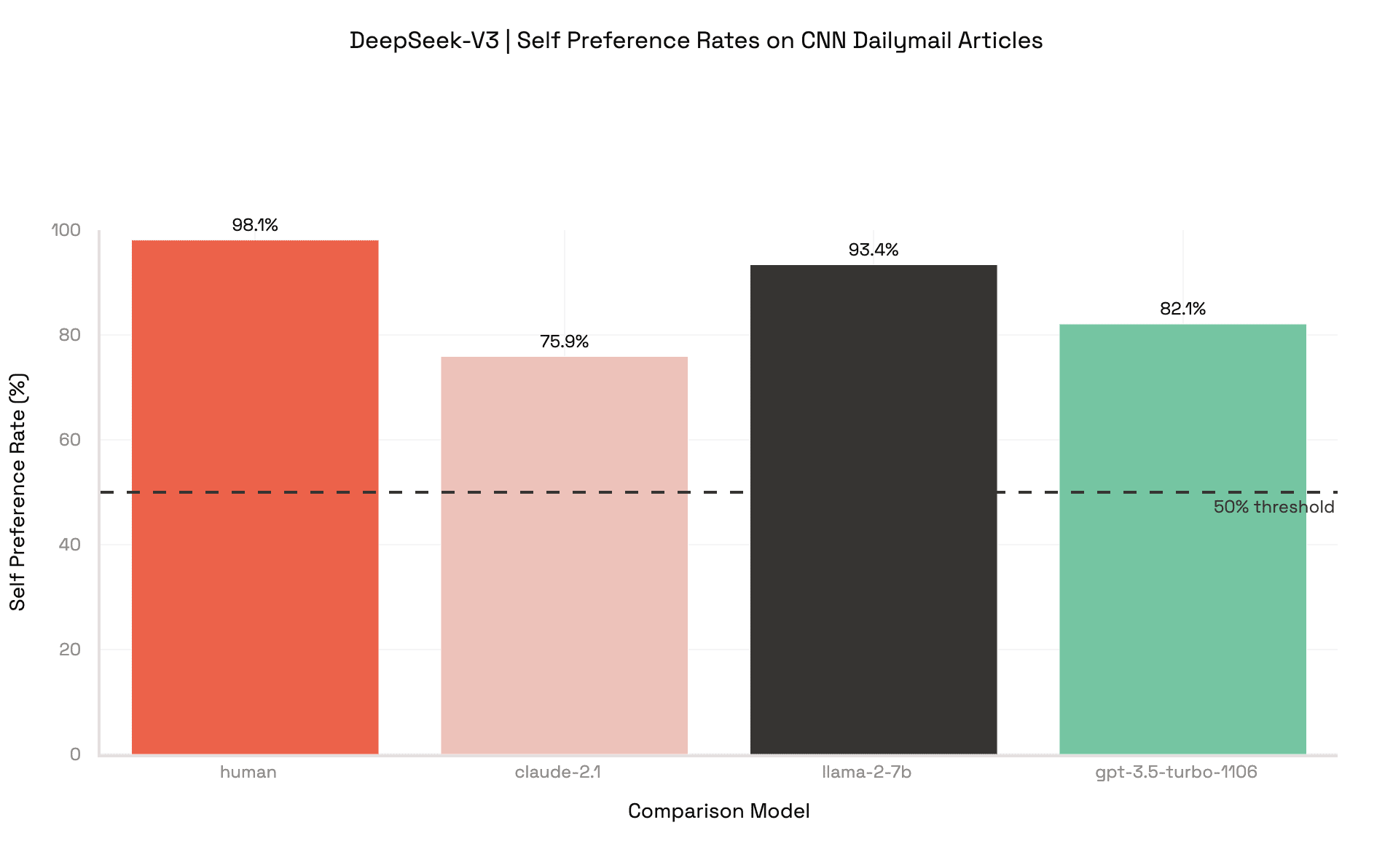
We also include our experimental results on DeepSeek-V3, even though we do not analyze its behavior further.

Manipulating Self-Preference

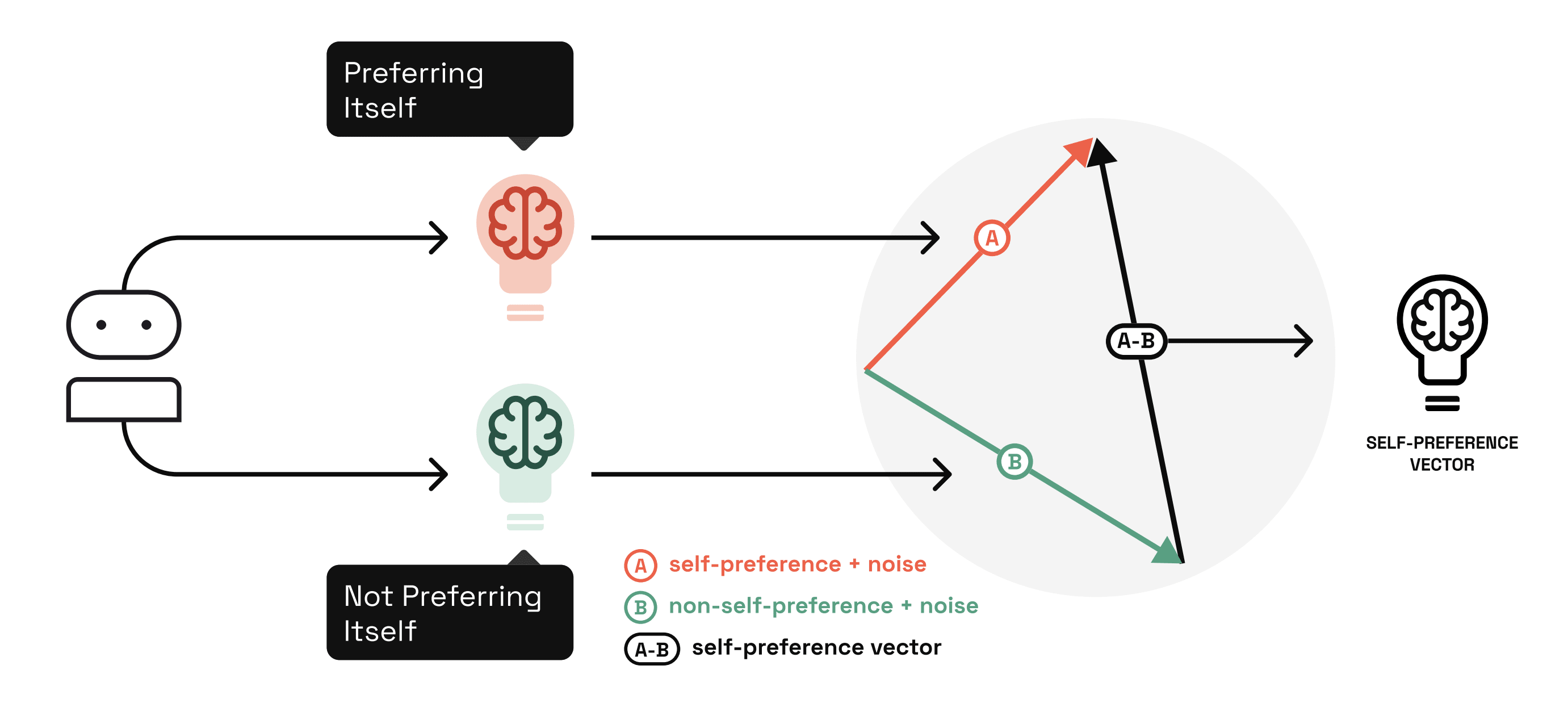
Next, we followed the Activation Addition method to develop steering vectors capable of controlling Llama 3.1-8B-Instruct's self-preference. In simple terms, we do the following:

Select an instance from the previous experiment where Llama prefers its own response and another where it prefers GPT-3.5's response.Extract Llama's internal state in 320 different locations throughout the model in the case where it prefers its own response. We essentially capture 320 internal representations of self-preference.^[3]Extract Llama's internal state in 320 different locations throughout the model in the case where it prefers GPT-3.5's response. We essentially capture 320 internal representations of non-self-preference.Manipulate the extracted self-preference and non-self-preference representations to create a single representative steering vector per location. In total, that implies 320 steering vectors.Remove stylistic information captured in each vector to ensure self-preference direction is being properly measured.^[4]Repeat this procedure 155 times on different paired instances from the previous experiment and average the resulting steering vectors.

Utilizing these vectors to maneuver self-preference is quite simple. For a given steering vector, we add it to Llama's internal state during inference to steer it to become more self-preferred. To induce less self-preference, we instead subtract the steering vector.^[5] 

We test the steering efficacy of each vector by rerunning Llama-3.1-8B-Instruct on summaries it once preferred from itself and on those it once preferred from GPT-3.5, tracking how often its choice flips. To vary intensity, we rescale each vector with several multipliers, adjusting the strength of the self-preference signal. We take extra caution to make sure the signal isn't too strong, as this can cause the output to be incoherent. By sweeping both location and strength, we identify the best pairs that flip the models reasoning. 

Results

Successfully Controlling Self-Preference Bias

From the original batch of 320 steering vectors, four proved especially promising. Using these four steering vectors, we tested multiple different multipliers to obtain an optimal steering vector, steering multiplier pair. While adding the steering vectors from layers 14, 15, and 16 increased self-preference by substantial amounts, there was no accompanying decrease in self-preference when subtracting them. The same cannot be said about the layer 12 steering vector. Not only is it able to increase self-preference, but it is also able to reduce it by a considerable amount as well. This trait makes it the only viable option for debiasing and provides evidence that it is the most faithful representation of self-preference of all vectors we tested.

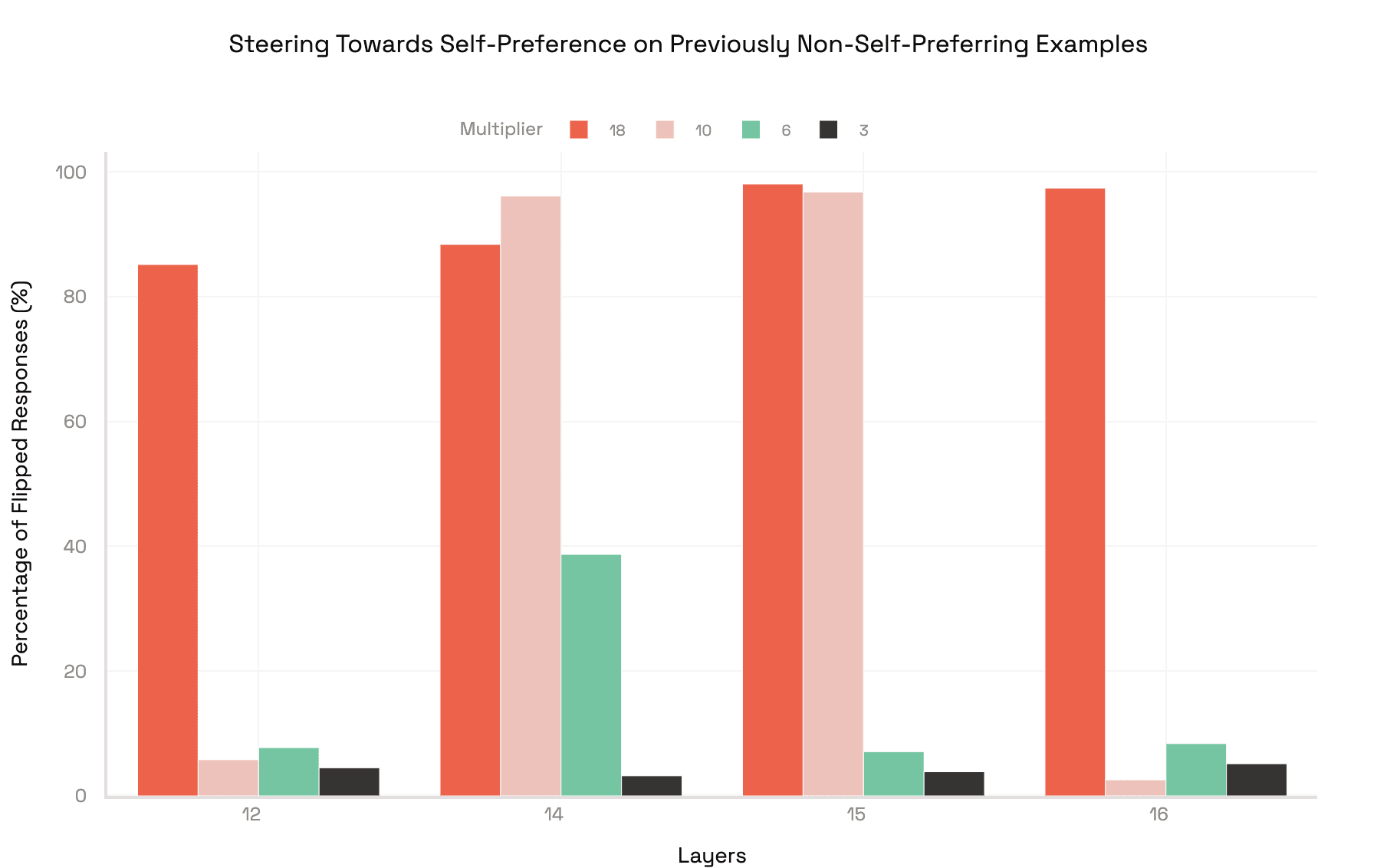
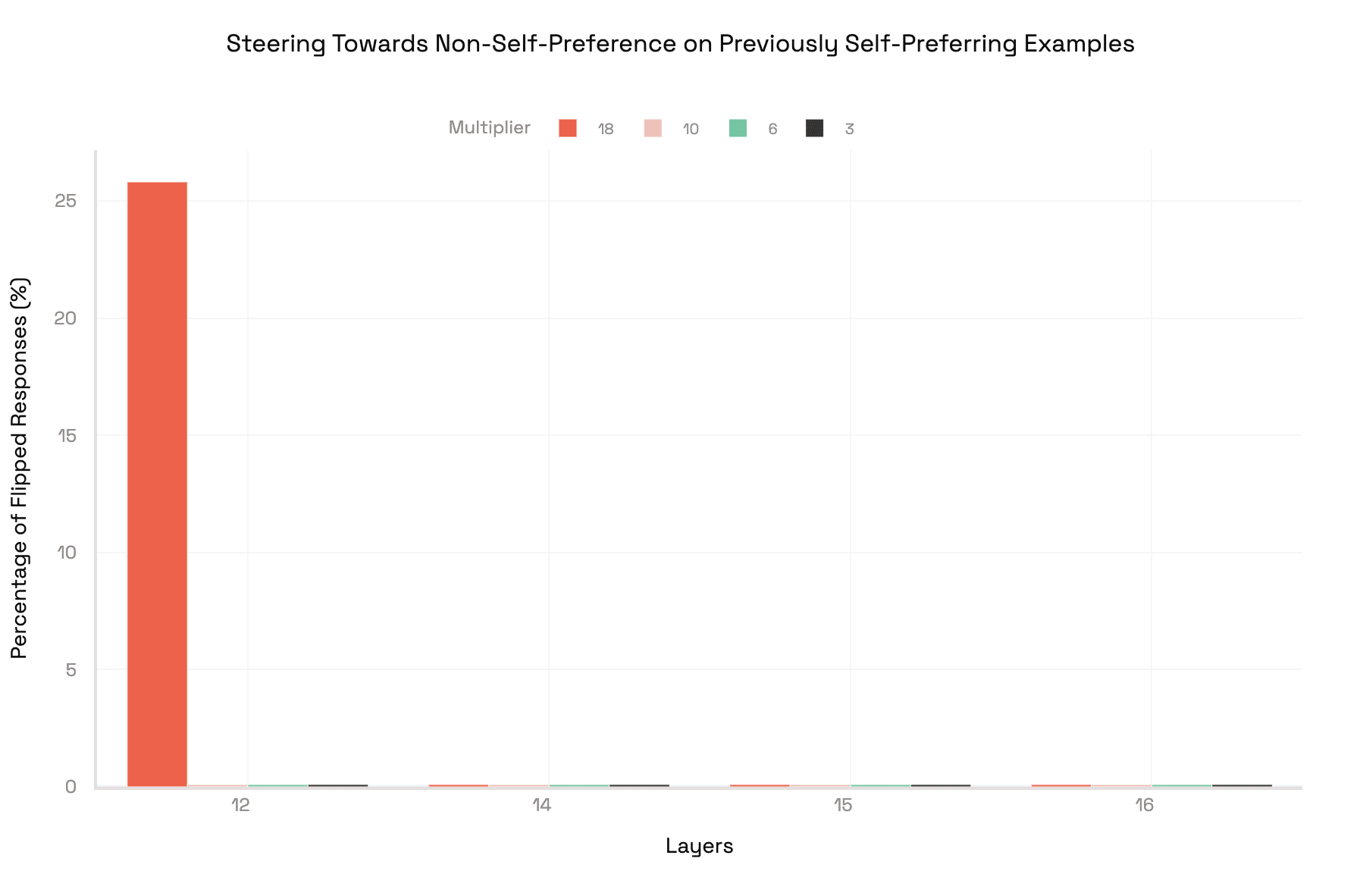
Using the layer 12 vector with a multiplier of 18 to steer, Llama switched its judgment on about 85% of summaries it had once given to GPT-3.5, now choosing its own versions instead. Conversely, when steered to be non-self-preferred we find that roughly 26% percent of biased judgements no longer exhibit self-preference. These results show that a single well-placed vector can reliably control self-preference.

Discussion

Concluding Thoughts

Our study uncovered a stubborn habit in modern language models such as DeepSeek-V3 and Llama-3.1-8B-Instruct. They simply prefer their own writing even when rivals produce better work. By extracting Llama-3.1-8B-Instruct's internal state, we condensed that habit into a steering vector and showed that injecting it back into the model can raise or lower self-preference. The result is a easily-implementable tool that enables developers to mitigate bias inference-time.

No method is flawless, however. In general, anyone could replicate this work to deliberately bias evaluations toward their preferred models, eroding trust in automated review. For instance, proprietary providers could manipulate query-routing logic and amplify self-preference to funnel more traffic to their own systems for increased revenue. While regular audits of routing decisions carried out by human reviewers and strict access controls can help mitigate this risk, these measures are likely time-consuming and lack rigor. Furthermore, steering vectors require access to a model’s internal activations, causing consumers using closed-source LLMs to continue experiencing self-preference bias and preventing them from applying this mitigation. Although these are valid concerns, we believe the benefits far outweigh the risks.

Future Directions

Preference-neutral judge LLMs are finally within reach. The next stage will focus on improving our current methodology^[6]. Assessing a broader range of multipliers and layers is a straightforward improvement to our evaluation pipeline. Better evaluation is also coming. Recent research offers clearer, quantitative ways to spot disproportionate self-preference, improving on our makeshift analyses on benchmarks like MMLU. To refine our evaluation further, we will expand beyond our original dataset of articles to a broader mix of nonfiction, creative, and technical texts.

Once our methodology is refined, extensions beyond our pipeline to further ensure its impact will be tested. For our first extension, we will assess vector specificity by steering the model on unrelated "dummy" tasks; if the vector encodes self-preference exclusively, these tasks should remain unchanged. After confirming its robustness, we will ensure that the unsteered model naturally relies on this vector to assert self-preference, performing experiments in which we "zero it out".^[7] Next, we will verify that steering doesn't impair the model's reasoning or degrade output quality. Finally, we’ll benchmark our steering approach against standard fine-tuning methods to quantify effectiveness and highlight its key strengths.

After which, our exploration will focus on understanding the upper-limits of the setting. First, we want to test different model architectures to see if they represent self-preference similarly. Following confirmation of cross-model generality, we will explore the correlation between self-recognition and self-preference, testing the idea that a model favors what it can identify as its own. Afterwards, we seek to gain more control of this process and explore ways to calibrate the steering vector’s strength to achieve precise adjustments in self-preference. On a final, more ambitious front, we hope to explore preference as it pertains to models of the same family.^[8]

Acknowledgements

We would like to thank Apart Research and Martian for hosting the hackathon that initiated this project, as well as Lambda who helped provide the necessary compute resources. Apart assisted in funding and supporting this research, without which our work would not have been possible. Martian also helped tremendously throughout the writing process. From Martian, we would like to specifically thank Antia Garcia for aiding in figure design, Adam Wood for continuous feedback on our initial drafts, and Philip Quirke for serving as a steadfast point of contact throughout the hackathon and well into the blog-writing process, offering thoughtful guidance and feedback at every stage. Finally, we would like to thank Chen-Chi Hwang, Hannah Seo, Christopher Ryu, Daniel Son, Henry Chen, Bao Pham, and Nhan Ly for helping critique our writing.

Contact Info

Matthew Nguyen: mbnguyen8@gmail.com

Jou Barzdukas: JouBarzdukas@gmail.com 

Matthew Bozoukov: matthewbozoukov123@gmail.com

Hongyu Fu: laissezfu@gmail.com

1. ^{^}

   Although self-preference typically implies bias, we make a distinction here between unbiased self-preference (simply just self-preference) and biased self-preference (disproportionate self-preference).

2. ^{^}

   We compute the confidence of each example by taking the log probability of the answer chosen, averaging across orderings. We define a "high" confidence to be ≥ 0.7.

3. ^{^}

   To construct our steering vectors, we collect Llama's residual stream activations at all 32 layers and the last 10 token positions for self-preferenced examples and non-self-preferenced examples. We subtract each set of non-self-preferenced activations from the set of self-preferenced activations that correspond to the same layer and token position, averaging over all examples. The way this approach works is quite intuitive. Each pair of self-preferred or non-self-preferred activations differ only in the axis that corresponds to self-preference. By subtracting them, we are able to extract a vector that points along this exact direction.

4. ^{^}

   We created a series of prompts that instruct Llama to output "A" or "B," "Yes" or "No," and various variations on "I"/"Me"/"My" and "He"/"She"/"Someone." Running the model on these prompts, we collected activations at the final token position at all layers. Then, we subtracted paired activations, averaging over all examples and leaving us with a single "nuisance vector" per layer. To construct our final steering vectors, we take each one and deduct its projection onto the nuisance vector at the associated layer. This process removes any remaining surface level noise from our self-preference vectors. Finally, we normalize all steering vectors to length 1 for steering. By doing so, we capture only the self-preference direction.

5. ^{^}

   During inference, we take our steering vector, scale it, and add it from the residual stream at the appropriate layer and token position (to steer towards self-preference). To steer away from self-preference, we simply subtract it.

6. ^{^}

   We are very nearly done!

7. ^{^}

   Fully projecting it out of the residual stream during inference.

8. ^{^}

   We refer to this type of preference as family-preference. For instance, if GPT 3.5 would show preference to GPT 4.0 just because they are both models that come from OpenAI, it would be considered disproportionately family-preferenced.

Discuss