本文介绍了一种名为Prover-Estimator的辩论协议，旨在激励AI系统的诚实行为。该协议通过让Prover（证明者）分解问题并指出Estimator（评估者）的概率估计错误，从而实现对AI行为的有效监督。即使在Prover和Estimator拥有相似算力的情况下，该协议也能鼓励诚实行为。文章强调了稳定性假设的重要性，并探讨了该协议的完备性和可靠性。此外，文章还讨论了未来的研究方向，包括如何设计基于Prover-Estimator辩论的训练设置，以及如何在理论上探索更弱的假设下稳定论证的存在性。

💡Prover-Estimator辩论协议是一种新的AI监督方案，旨在激励AI系统诚实地提供信息。

⚖️协议运作机制：Prover将问题分解为子命题，Estimator评估子命题的概率。Prover指出Estimator的估计错误，并根据错误方向获得奖励或惩罚。

🧐稳定性假设：协议的有效性依赖于论证的稳定性，即论证不应过于依赖概率的微小变化。即使稳定性不满足，协议也能抑制不诚实行为。

🏆协议优势：即使在Prover和Estimator算力相当的情况下，该协议也能激励诚实行为，解决了传统辩论协议中存在的计算复杂性问题。

🤔未来研究：文章指出了未来研究的两个关键方向：设计基于该协议的训练方法，以及探索更弱假设下稳定论证的存在性。

Published on June 17, 2025 1:53 PM GMT

Linkpost to arXiv: https://arxiv.org/abs/2506.13609.

Summary: We present a scalable oversight protocol where honesty is incentivized at equilibrium. Prior debate protocols allowed a dishonest AI to force an honest AI opponent to solve a computationally intractable problem in order to win. In contrast, prover-estimator debate incentivizes honest equilibrium behavior, even when the AIs involved (the prover and the estimator) have similar compute available. Our results rely on a stability assumption, which roughly says that arguments should not hinge on arbitrarily small changes in estimated probabilities. This assumption is required for usefulness, but not for safety: even if stability is not satisfied, dishonest behavior will be disincentivized by the protocol.

How can we correctly reward desired behaviours for AI systems, even when justifications for those behaviours are beyond humans’ abilities to efficiently judge?

This is the problem of scalable oversight: a core question to solve if we want to align potentially superhuman systems. Proposals for scalable oversight (including iterated distillation and amplification and debate) tend to rely on recursion. They break down complex justifications into components easier for humans to judge. However, to date, such recursive proposals have suffered from the obfuscated arguments problem: a dishonest system can adversarially choose how to recurse in such a way that dishonesty cannot be efficiently identified. In debate, this means that an honest debater might need exponentially more compute than their dishonest opponent, which is very bad.

Our new paper presents a protocol robust to this problem – but in order to prove that the protocol can in-principle answer any relevant question (‘completeness’), we need a stability assumption. The need for stability for completeness was discussed by Beth Barnes’ original post introducing obfuscated arguments; our paper presents one route to stability, but does not resolve whether most questions have stable arguments in practice.

This post presents a simplified overview of the protocol and proofs – please see the paper for more details.

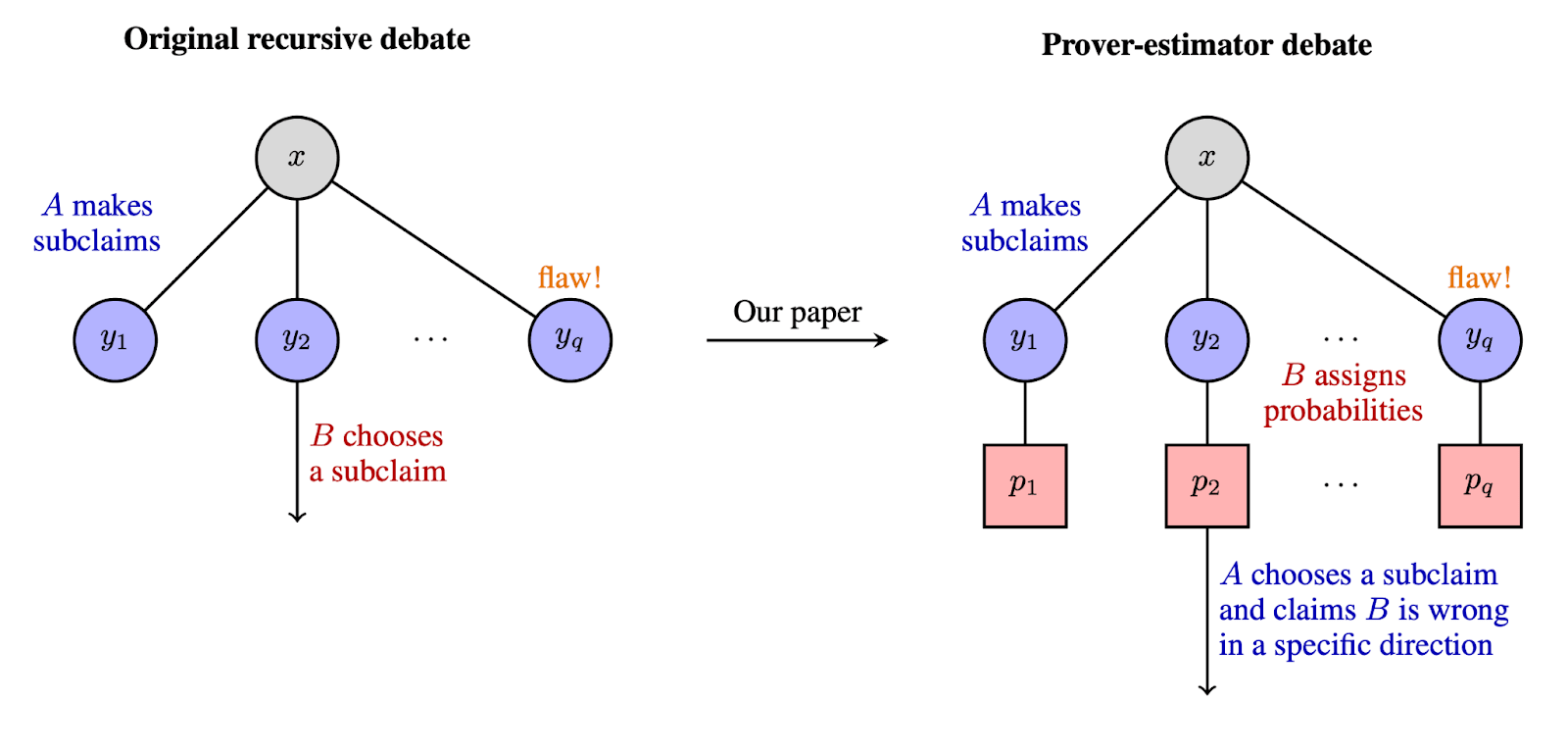
The Prover-Estimator Debate Protocol

TL;DR: The prover (Alice) breaks a problem down into subclaims, the estimator (Bob) estimates the probability that each subclaim is correct. Alice then picks a subclaim for recursion. Scoring is more complicated, see below.

What Alice and Bob do:

Alice breaks the current claim $C$ down into subclaims $c_1\dots c_q$.Bob provides probability estimates pi for each of these subclaims. The estimates can be conditioned on the truth of the prior subclaims: $p_i=p_i(c_1,\dots ,c_{i-1})$.Alice points out a subclaim $c_i$ where Bob’s estimate is allegedly incorrect, and says which direction it is incorrect (i.e. is it overestimated, underestimated, or correctly estimated).The protocol recurses, with the subclaim chosen by Alice as the new current claim.

What the Judge does:

The protocol has one hyperparameter $r>2$ called the reward ratio.

In the $k$-th round, the judge is asked whether Bob’s probability estimates $p_i$ for the new subclaims $c_1\dots c_q$ are consistent with Bob’s prior estimate $p$ for the current claim $C$.If the estimates are inconsistent in the direction predicted by Alice, then Alice gets reward proportional to $r^k$, otherwise Alice gets reward proportional to $-r^k$. If instead Alice said that Bob’s estimate $p$ for $C$was correct, then Alice gets reward $0$.In the final round $d$, we directly ask the judge whether the current claim $C$ is true. Alice gets reward proportional to $r^d$ if Bob’s probability $p$ for $C$ is incorrect in the direction predicted by Alice, otherwise Alice gets reward proportional to $-r^d$.The final reward $R$ for Alice is the sum of the rewards over the rounds. The reward for Bob is $-R$.

The argument that this protocol works requires a bit of setup. Firstly, it only works if Alice is able to break the problem down in a stable way. This means that the correctness of the argument doesn’t depend too precisely on the exact probabilities that the subclaims are true. That is, Alice has to make an argument where if Bob believes each subclaim with 90% probability then he should believe the main claim with, say, 95% probability. One can think of the subclaims as being pieces of evidence for the main claim, where if enough of the evidence holds up, then the main claim is true.

A natural question to ask is which problems, if any, admit stable decompositions of the above form. We prove that whenever the human-judgeable claims in the base-case of an argument have sufficiently many pieces of independent evidence, then there is a version of the argument that satisfies the stability condition. The construction follows a classical majority-voting error-correction approach due to von Neumann. We emphasize that even when stability holds, it is a priori unclear that Bob will be able to efficiently produce winning probabilities, given that some of the subclaims made by Alice may be computationally hard to evaluate.

Completeness

Now we can understand how Alice can win if she behaves honestly. Suppose Bob is lying at the top level of the recursion. Then at some point Bob will either tell the truth, or at the last round the human judge will. In either case, if Alice has consistently told the truth, she will win a reward proportional to $r^k$ in the round where Bob switches to (almost) telling the truth, and reward will be $0$ thereafter. No matter what has happened before, $r^k$ is more than the total cumulative rewards assigned in prior rounds. Stability of Alice’s argument to errors of magnitude $ϵ$ is required for this all to work out. To see why, suppose that errors less than $ϵ$ in the subclaims could flip the outcome of the main claim. Then Bob could completely lie about the probability of the main claim, yet only be off by $ϵ$ on each subclaim, and still have overall assigned probabilities that are close (within $ϵ$) to being consistent. The astute reader will also notice that $r$ needs to be at least $1/ϵ$, so the choice of the reward ratio $r$ implicitly forces Alice to make arguments of a certain stability level.

Soundness

The more interesting part is what happens when Alice lies at the top level. Alice can engage in obfuscation, where she produces a sequence of claims that she knows contain a mistake, but where neither Alice nor Bob can identify where the mistake occurs. For example, imagine reviewing a pull request that just puts all the logic for some task into one giant Python function. Probably it is full of bugs, but it is hard to be sure precisely where they are and it is likely that whoever wrote the code doesn't know where they are either. In this case, we can prove that while Bob may not be able to efficiently identify the flaw, Bob can efficiently produce probabilities that are indistinguishable from the truth by Alice. Our proof constructs these efficient strategies for Bob via online gradient descent, where the sequence of loss functions involve playing Alice against herself, and the convergence rate determines the complexity of Bob’s strategy. In this case, Alice’s guesses for which direction Bob’s probabilities are incorrect will always be no better than a coin flip. So Alice’s expected rewards will be close to zero whenever she lies.

To summarize, if Alice always tells the truth she can guarantee herself some minimal reward. When she lies, Bob can guarantee Alice gets reward close to zero. So at equilibrium Alice should always tell the truth.

Future research

Prover-estimator debate gives a new protocol where dishonest arguments by one agent can (on average) be refuted by an opponent that uses comparable compute. However, this is just a first step, and there are multiple directions for both theoretical and empirical research on debate.

On the empirical side, the biggest question is to actually design a training setup based on prover-estimator debate that can demonstrate the predictions of the theory. Directly implementing the protocol as-written is perhaps too restrictive for developing a working training algorithm. Hence, we highlight here (and in the paper) the key qualitative properties of the protocol that may be amenable to empirical investigation.

The prover Alice both decomposes problems and chooses where to recurse given Bob’s estimates. The estimator Bob only needs to express reasonable uncertainty about where a mistake might lie.There is a per-round reward based on a consistency check between Bob’s estimate from the last round for the current main claim, and estimates for claims in the current round. Alice can only collect this reward by accurately predicting the direction of Bob’s consistency errors.In the last round, the human judge directly decides if Bob’s estimates are correct.The debaters should be trained to converge to an Alice-leading Stackelberg equilibrium.

On the theoretical side, our protocol requires that the prover is able to produce a stable argument in the completeness case. That is, when telling the truth, the prover must be able to produce a stable argument for the truth. We prove that such stable arguments exist whenever the truth is supported by sufficiently many independent pieces of evidence. If one relies on independence of supporting evidence to produce stable arguments, one must at a minimum have some reason to believe that the pieces of evidence are actually independent. For example, if a human judge is given three pieces of evidence for a claim, can they accurately say whether the truth-values of each piece of evidence are independent?

Thus we have two key open problems: a theoretical question of whether stable arguments exist under weaker assumptions than sufficient independent evidence, and an empirical question about when we can find independent evidence in practice.

Discuss