关键词：量子计算，数字量子模拟，低能量子空间

导  读

本文是发表在 Quantum 上的论文 Complexity of Digital Quantum Simulation in the Low-Energy Subspace: Applications and a Lower Bound [1]的详细解读。该项研究由哈佛大学博士生龚维元，北京大学博士生周烁，北京大学助理教授李彤阳合作完成。

论文系统分析了当初态被限制在低能量子空间中时，基于乘积公式（product formula）的数字量子模拟算法的误差与复杂度是如何得到改进的，开展数值实验佐证了理论，并且给出了查询复杂度（query complexity）的一个下界。

← 扫码跳转论文

论文地址：

https://arxiv.org/abs/2312.08867

01

背景与动机

量子模拟是量子计算机最原初的应用动机之一。自从上世纪八十年代，Feynman 提出用计算机模拟物理学以来，诸多量子模拟算法开始涌现。其中极为重要的一类基于李代数中的乘积公式（product formula），比如将演化时间拆成极短单步  后，我们可以使用 Suzuki-Trotter formula 来近似时间演化算符  ，  [2]： 其中，而相对容易用量子门实现。对于足够大的步数（Trotter number），我们有。

如果采用算符之差的谱范数（spectral norm）来度量量子模拟的误差，从而决定合适的  使得误差控制在目标  以内，我们会发现误差上界往往依赖于哈密顿量的谱范数，也即特征值的模中最大者[3]： 而实际中很多量子物理过程往往发生在哈密顿量的基态能级附近，其能量阈值  远低于能谱的最高能级，这意味着在低能量子空间中我们有望改进量子模拟的误差。2021年洛斯阿拉莫斯国家实验室的 Şahinoğlu 和 Somma[3]证明了当初态被限制在低能量子空间中时， 其中  为投影算符，  是略高于低能量子空间阈值  “有效低能量模”。相应地，步数  （Trotter number）和量子门数（gate complexity）会有所减少。

02

贡  献

本篇工作延伸了上文的框架，证明了低能量子空间中随机编译（qDRIFT），随机排列（random permutation）与对称性保护（symmetry protection）的乘积公式误差与复杂度对我们关心的物理量的依赖将得到改进[1]。

下表为关于  （Trotter number）的结果概览，我们可以看到，低能量子空间限制使粒子数  、演化时间  与目标精度  的幂次依赖以 trade-off 或者 decoupling 的方式得到改进，同时一部分对于粒子数  换言之谱范数的依赖被阈值  取代。

首先介绍关于  -local 自旋模型的算符能量子空间投影/泄露定理[5]，作为全文的基本引理： 其中  可以代入我们想要研究的算符，其余参数依赖格点自旋模型。注意不等式右侧收敛需要一个预备工作：将所有局域相互作用量平移到半正定  ，这只会对时间演化算符产生一个全局相位的改变。

总的来说，我们遵循以下的理论框架： 投影误差其中 \bar 记号表示将公式中的所有的  左右两侧各加上投影算子，即  。  可以理解成事后确定的辅助变量，一个关键的观察是  。

    第一项投影误差可以通过基本引理推导得出，往往与  负相关。

    第二项可以通过将前人工作中  替换成  直接得出。

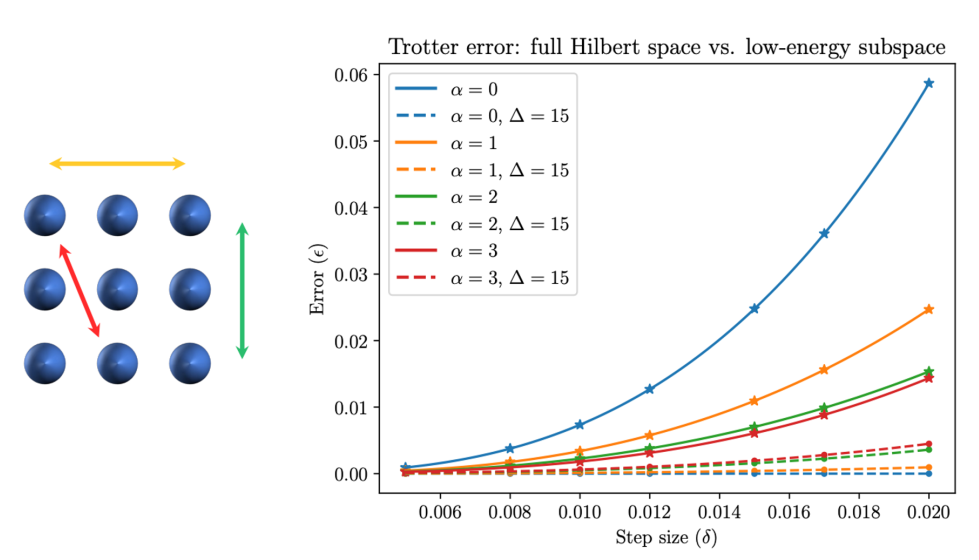
对于 qDRIFT 和 randomized product formula 两种带随机性的方案，我们通过构造矩阵鞅（matrix martingale）给投影误差提供了上界。而对于 symmetry transformation，我们构造了一个带  参数的幂次依赖。最终我们以一种类似均值不等式的方式，令其中主要两项相近来确定合适的  得到尽可能小的误差上界。

同时我们就海森堡自旋模型（Heisenberg spin model）展开了相应的数值试验。

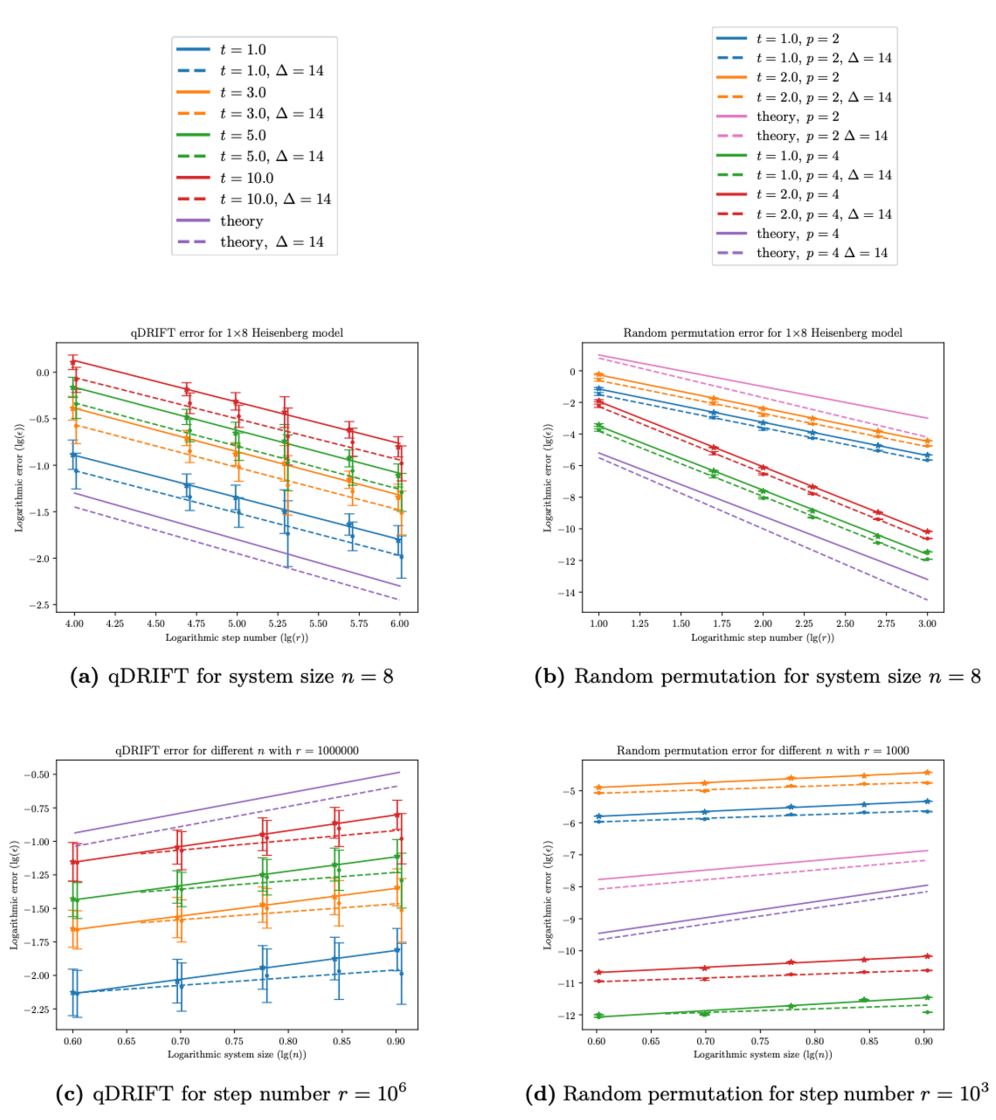
此外我们的结果在初态制备收到热化（thermalization）影响下仍然具有鲁棒性，对于 power-law 模型也做了具体探索。最后我们通过将问题规约为计算字符串的 parity[3]，给出了低能量子空间量子模拟算法查询复杂度（query complexity）的一个下界。

代码

我们的代码开源在：

https://github.com/Qubit-Fernand/Digital-Quantum-Simulation

参考文献

[1] Weiyuan Gong, Shuo Zhou, Tongyang Li. "Complexity of Digital Quantum Simulation in theLow-Energy Subspace: Applications and a Lower Bound". Quantum 8, 1400 (2024). arXiv:2312.08867.

[2] Masuo Suzuki. "Fractal decomposition of exponential operators with applications to many-body theories and Monte Carlo simulations". Physics Letters A 146, 319–323 (1990).

[3] Dominic W. Berry, Graeme Ahokas, Richard Cleve, and Barry C. Sanders. "Efficient quantum algorithms for simulating sparse Hamiltonians". Communications in Mathematical Physics 270, 359–371 (2007). arXiv:quant-ph/0508139.

[4] Burak Şahinouglu and Rolando D. Somma. "Hamiltonian simulation in the low-energy subspace". npj Quantum Information 7, 119 (2021). arXiv:2006.02660.

[5] Itai Arad, Tomotaka Kuwahara, and Zeph Landau. "Connecting global and local energy distributions in quantum spin models on a lattice". Journal of Statistical Mechanics: Theory and Experiment 2016, 033301 (2016). arXiv:1406.3898.

图文 | 周烁

PKU QUARK Lab

关于量子算法实验室

量子算法实验室 QUARK Lab (Laboratory for Quantum Algorithms: Theory and Practice) 由李彤阳博士于2021年创立。该实验室专注于研究量子计算机上的算法，主要探讨机器学习、优化、统计学、数论、图论等方向的量子算法及其相对于经典计算的量子加速；也包括近期 NISQ (Noisy, Intermediate-Scale Quantum Computers) 量子计算机上的量子算法。

实验室新闻：#PKU QUARK

实验室公众号：


课题组近期动态

—   版权声明  —

本微信公众号所有内容，由北京大学前沿计算研究中心微信自身创作、收集的文字、图片和音视频资料，版权属北京大学前沿计算研究中心微信所有；从公开渠道收集、整理及授权转载的文字、图片和音视频资料，版权属原作者。本公众号内容原作者如不愿意在本号刊登内容，请及时通知本号，予以删除。

点击“阅读原文”转论文链接