本文探讨了大型语言模型（LLMs）在近似所罗门诺夫归纳方面的表现。研究者通过实验，使用GPT-2系列模型，评估其在预测来自通用分布的序列方面的能力，并与专门训练的所罗门诺夫归纳Transformer（SIT）和统计模型进行比较。实验结果表明，LLMs在无需特定任务训练的情况下，也能在一定程度上执行所罗门诺夫归纳，但更大模型并不一定表现更优。研究旨在验证LLMs是否可以被视为对所罗门诺夫归纳的近似，并为这一理论观点提供实证支持。

🤔 研究背景：文章探讨了LLMs是否可以被视为近似所罗门诺夫归纳，通过实验验证LLMs在预测通用分布样本方面的能力。

💡 实验方法：作者使用GPT-2系列模型，以及专门训练的Solomonoff Induction Transformer (SIT) 和统计模型，在来自通用分布的序列上进行评估，并比较它们的对数损失。

📊 实验结果：LLMs在无需特定任务训练的情况下，表现出对所罗门诺夫归纳的合理性能，但更大模型并未表现出持续的优势。

🧐 结论与讨论：LLMs能否被理解为近似所罗门诺夫归纳，仍存在争议。文章认为，LLMs可能通过其他机制实现对通用分布的预测，但仍需进一步研究。

Published on June 5, 2025 5:45 PM GMT

Epistemic status: One week empirical project from a theoretical computer scientist. My analysis and presentation were both a little rushed; some information that would be interesting is missing from plots because I simply did not have time to include it. All known "breaking" issues are discussed and should not effect the conclusions. I may refine this post in the future.

[This work was performed as my final project for ARENA 5.0.]

Background

I have seen several claims^[1] in the literature that base LLM in-context learning (ICL) can be understood as approximating Solomonoff induction. I lean on this intuition a bit myself (and I am in fact a co-author of one of those papers). However, I have not seen any convincing empirical evidence for this model. 

From a theoretical standpoint, it is a somewhat appealing idea. LLMs and Solomonoff induction both face the so-called "prequential problem," predicting a sequence based on a prefix seen so far with a loss function that incentivizes calibration (the log loss; an LLM's loss function may also include other regularization terms like weight decay). Also, ICL is more sample efficient than pretraining. For me, this dovetails with Shane Legg's argument^[2] that there is no elegant universal theory of prediction, because an online predictor must be complex to learn complex sequences successfully. LLM pretraining is a pretty simple algorithm, but LLM ICL is a very complicated algorithm which leverages a massive number of learned parameters. This is an incomplete argument; Solomonoff induction is a highly general sample efficient algorithm for the prequential problem, as is LLM ICL, but that does not mean they are meaningfully connected. In fact, they are optimized for different distributions: the universal distribution versus the distribution of text on the internet. Arguably, the later may be a special case of the former with an appropriate choice of universal Turing machine (UTM), but I find this perspective to be a bit of a stretch. At the very least I expect LLM ICL to be similar to a universal distribution conditioned on some background information.

In order to gather some empirical evidence, I adapted this approximate universal distribution sampler from Google DeepMind. They used the samples to train a transformer to directly approximate Solomonoff induction in-context, which I will call the Solomonoff Induction Transformer (SIT).

Can you really sample from the universal distribution?

You cannot actually sample from the universal distribution because of runtime limitations, but it is in some sense easier to sample than to compute conditionals. You just sample a random program and then run it to produce its output.

Technically, the GDM repository trains a transformer to approximate a normalized version of the universal distribution. 

GDM tried the SIT out on some easier tasks, predicting sequences sampled from variable order Markov sources and context-free grammars, and showed that its learning transferred well. In a sense this demonstrates the generality of the universal distribution.

I am interested in the opposite question: if we take a transformer that was trained on a different task (text prediction) will it perform well at Solomonoff induction?^[3]

I investigated this question using the gpt2 series of models from huggingface.

This was an attempt to falsify the hypothesis that LLMs can be seen as approximating Solomonoff induction; it would seem to be a pretty baseless claim if they could not even "perform Solomonoff induction" reasonably well.

Methodology

I took 10,000 samples from the universal distribution approximation with an alphabet size of 2^[4]. I computed the ln loss for the SIT, a series of increasingly large gpt2 models, and some statistical (context-tree weighting) models trained on 10,000 independent samples as a baseline. The latter are essentially k-Markov models.

Here are some example program / output pairs. The models only see the outputs.

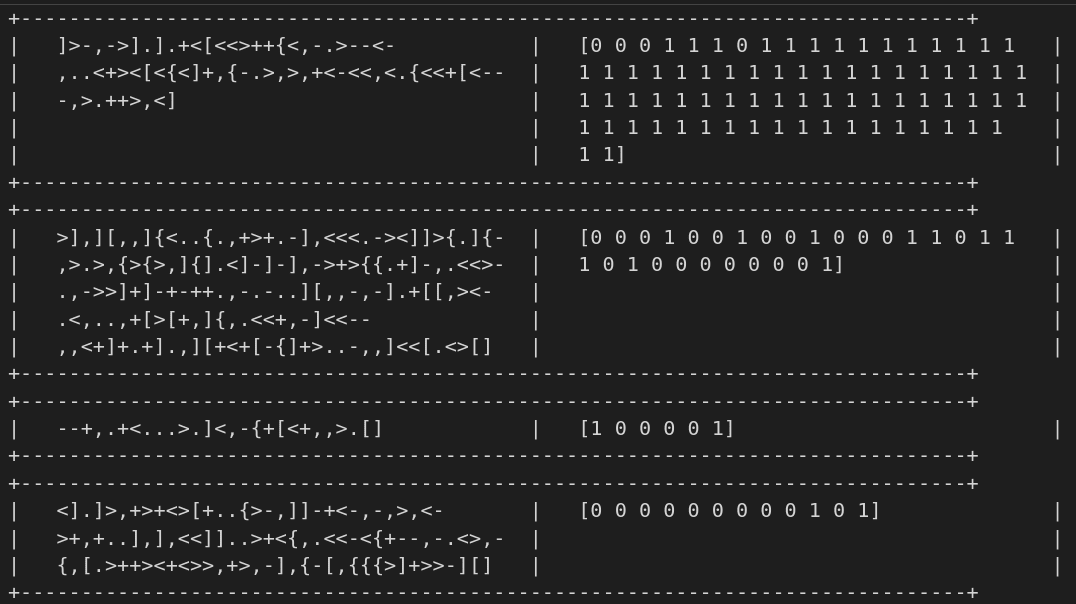
I fed the sequences to the LLMs in comma-separated binary. I was initially worried that they may not be familiar with binary data, but a quick sanity check with gpt2 indicated that an English encoding (zero,one,zero,...) did not improve performance. I restricted the LLM predictions to {0,1} and renormalized to compensate for their larger alphabet sizes.

I trained my own SIT, but only for 52,000 steps (GDM trained for 10,000 but I did not have the time/resources). So the SIT results should not be taken too seriously. However, its loss did not seem to be improving much beyond my checkpoint. 

Results

The following plot shows the average ln loss at each sequence position.

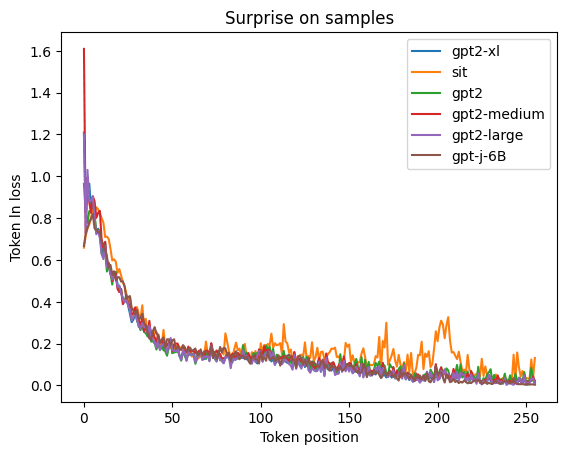
The following plot is the cumulative sum of the preceding plot, which provides a sort of measure of overall performance. It is a bit misleading because not all sequences are the same length. A better measure would be average cumulative ln loss, not cumulative average ln loss.

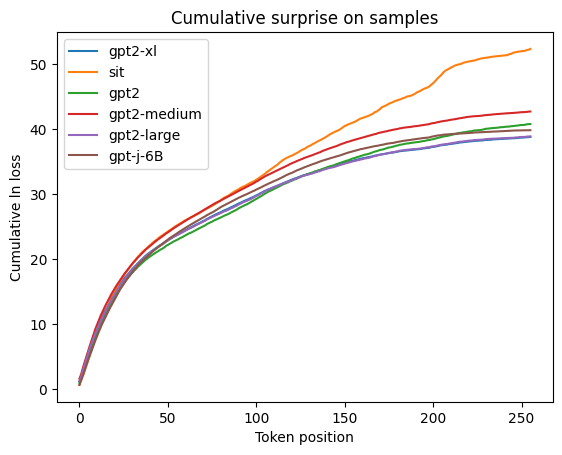
It seems strange that the SIT performs so badly at large sequence positions. Actually, the vast majority of sequences are shorter. This means that the cumulative ln loss at earlier sequence positions is much more important.

 The average total ln loss of each model is given below (with baselines):

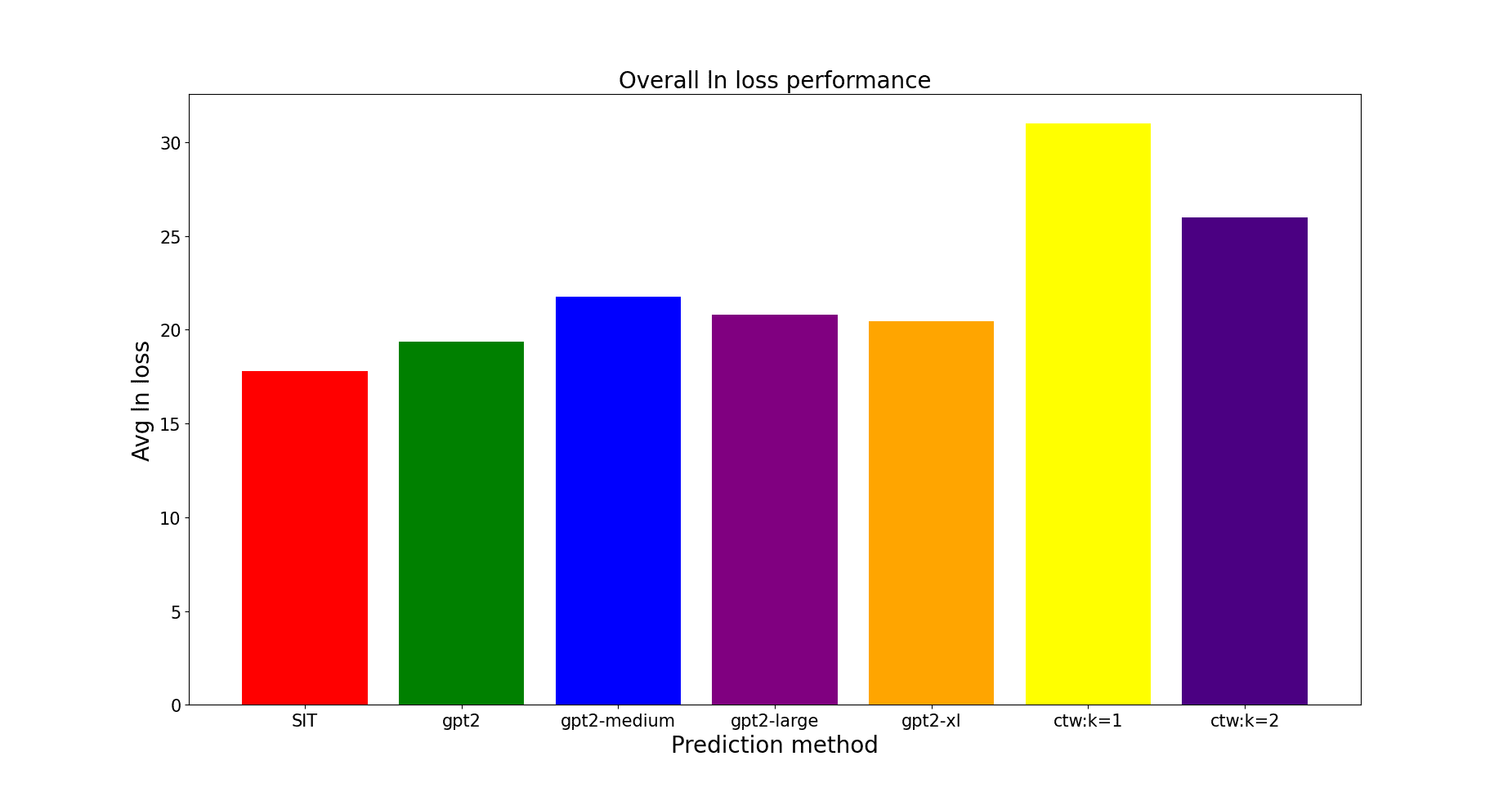
So the SIT is best performing, but not by much. All the transformers easily destroy the k-Markov models (the 0-Markov model would have ruined the scaling of the y-axis). Further increasing k does not help much. 

As an additional baseline, we can compare a very loose upper bound on the universal distribution computed from the (shortened) length of the sampled program (which the models do not have access to). Here, the x component of the points corresponds to the length of the output, and the y component corresponds to the upper bound on the ln loss of the universal distribution M for that specific sample. The comparison with the transformer models is not strictly correct because of the issues with sequence termination discussed above, but I think this still provides a rough sanity check.

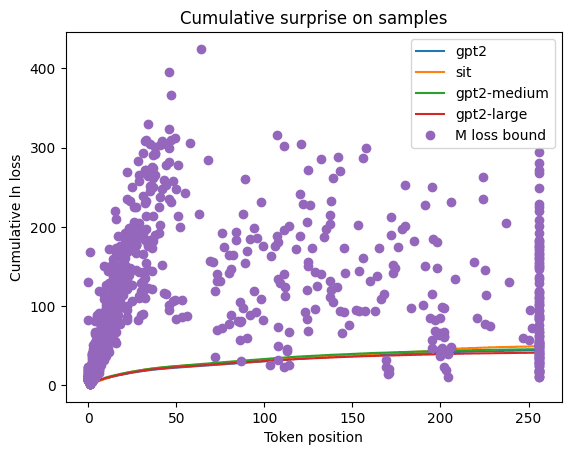
Conclusions

Surprisingly, it seems that LLMs do perform reasonably well at Solomonoff induction without any (?) task-specific training. However, larger models do not consistently perform better. Perhaps this is because their stronger inductive bias does not favor this task? In fact, the larger models do seem to have a slight edge on long sequences, which provides some support for this interpretation (maybe they are better at Solomonoff induction, but take longer to realize that is what they should be doing).

It is still unclear to me whether LLMs can be understood as approximating Solomonoff induction in-context or "do something else" that happens to allow them to perform reasonably well at Solomonoff induction. 

1. ^{^}

   [DRDC23] Deletang, Gregoire ; Ruoss, Anian ; Duquenne, Paul-Ambroise ; Catt, Elliot ; Genewein, Tim ; Mattern, Christopher ; Grau-Moya, Jordi ; Wenliang, Li Kevin ; u. a.: Language Modeling Is Compression. In: , 2023 

   [LHWH25] Li, Ziguang ; Huang, Chao ; Wang, Xuliang ; Hu, Haibo ; Wyeth, Cole ; Bu, Dongbo ; Yu, Quan ; Gao, Wen ; u. a.: Lossless data compression by large models. In: Nature Machine Intelligence (2025), S. 1–6 

   [WaMe25] Wan, Jun ; Mei, Lingrui: Large Language Models as Computable Approximations to Solomonoff Induction, arXiv (2025). — arXiv:2505.15784 [cs] 

   [YoWi24] Young, Nathan ; Witbrock, Michael: Transformers As Approximations of Solomonoff Induction, arXiv (2024). — arXiv:2408.12065 [cs] 

2. ^{^}

   [Legg06] Legg, Shane: Is there an elegant universal theory of prediction? In: Proceedings of the 17th international conference on Algorithmic Learning Theory, ALT’06. Berlin, Heidelberg : Springer-Verlag, 2006 — ISBN 978-3-540-46649-9, S. 274–287

3. ^{^}

   By the informal phrase "perform well at Solomonoff induction" I mean "perform well at predicting samples from the universal distribution."

4. ^{^}

   Note this is not directly comparable to most results in GDM's paper. They typically used an alphabet size of 128. I restricted to a binary alphabet because I did not want to deal with tokenization issues for the LLMs, which would have obfuscated their true potential at this task. 

Discuss