来源:雪球App,作者: 十年书禅,(https://xueqiu.com/4041738962/297039673)
芒格说过一句话:“长远来看,股票的回报率很难比发行该股票的企业的年均利润高很多。如果某家企业40年来的资本回报率是6%(即ROE6%),你在这40年间持有它的股票,那么你得到的回报率不会和6%有太大的差别——即使你最早购买时该股票的价格比其账面价值低很多。相反地,如果一家企业在过去二三十年间的资本回报率是18%,那么即使你当时花了很大的价钱去买它的股票,你最终得到的回报也将会非常可观。”
网上和股票群里,经常有同学探讨这句话,感到难以理解这句话。最常见的迷糊之处是:净资产收益率(ROE)是“净利润/净资产”,而大多数情况下,二级市场投资者是无法以净资产的市值买入股票的,而是以某个市净率PB买入股票的,所以投资者获得的投资收益率是“净利润/(PB*净资产)”。投资者看起来根本无法获得与ROE接近的收益率。
其实,芒格讲的这句话,有3个前提,大家不要忽略了:
1、投资期要足够长。只有投资期足够长,此结论才可能成立。
2、企业在一个较长的时期内,保持一个ROE不变。或者对这段时期计算出一个复合年化的ROE。
3、投资期内,既不出金也不入金。或者通过等效的方法消除了出入金的影响。
这样我们就可以通过以下的步骤,来理解芒格老先生的这段话。
b0:表示期初的净资产,即我们买入股票时企业的净资产。
j: 表示ROE
n: 表示投资期年数
k0: 表示买入时的市盈率,即期初的市盈率
kn:表示第n年末卖出股票时的市盈率,即期末市盈率
可以推算出:
期初净利润=b0*j
买入时的市值=k0*b0*j
第n年的净利润=b0*j*(1+j)^n
卖出时的市值=kn*b0*j*(1+j)^n
“期末市值/期初市值”的倍数=“卖出时的市值”除以“买入时的市值”=(kn/k0)(1+j)^n
以上倍数开n次方之后,再减去1,就是投资者在n年中获得的复合年化投资收益率。
先来看一个特例:当kn=k0的时候,即卖出时的市盈率与买入时的收益率相等时(即期初和期末的估值水平没有发生变化),以上倍数值变成 (1+j)^n。倍数值开n次方之后,等于(1+j)。再减去1,就是j。所以投资期间的复合年化投资收益率就是净资产收益率j。
那么当卖出时的市盈率与买入时的市盈率不相等,甚至相差较大时,芒格说的话还正确吗?
按芒格老先生的原话,即使买入时价格较低或较高,这个结论都应该成立的。
“期末市值/期初市值”=(kn/k0)(1+j)^n
这个倍数开n次方之后,等于:【(kn/k0)开n次方】*(1+j)
复合年化收益率=【(kn/k0)开n次方】*(1+j)-1
这里要用到一个数学常识:一个数字,无论是大于1还是小于1,在开n次方的时候,当n越来越大,开方的结果就越来越接近于1。
所以随着n的增大,【(kn/k0)开n次方】就会越来越接近1。而我们计算的复合年化收益率就会越来越接近j。
下表演示了在不同的 kn/k0 比值下,当n越来越大的时候,开方的结果逐步逼近1的情况:
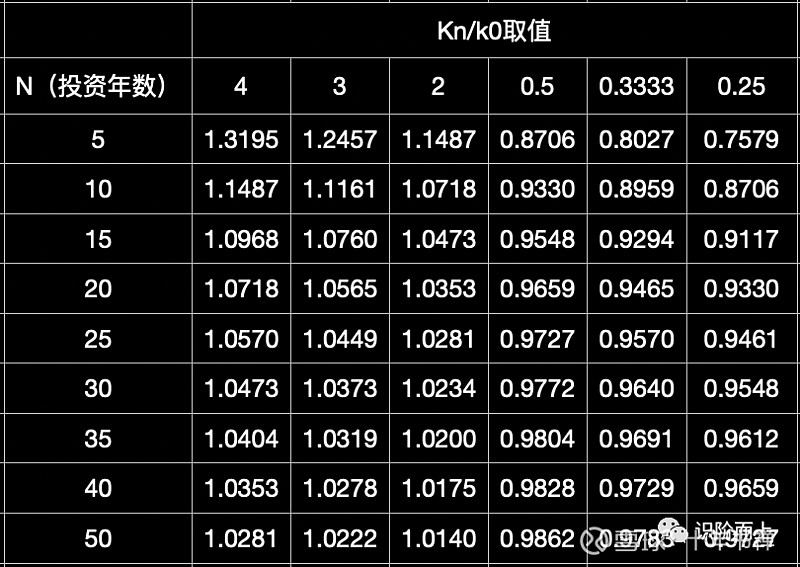
结论:只要满足了文章开头所说的三个前提,芒格先生的话就是正确无疑的。
即:长期持有一家企业的投资收益率,会与企业的ROE接近。买入时价格高了一些,或者低了一些,对这个结论影响不大,比如现在的$贵州茅台(SH600519)$ 。
注:转载于企鹅号“识阶而上”。

