20世纪中叶，纳什均衡（Nash Equilibrium）成为博弈论的基石，其假设所有参与者完全理性且信息透明。然而，现实中的决策常包含噪声和误差，例如：

投资者在股市中的非理性抛售；

消费者面对多个品牌时的随机选择。 

这些现象无法用纳什均衡完美解释。

1995年，经济学家 Richard McKelvey 与 Thomas Palfrey 提出了量子响应均衡均衡（Quantal Response Equilibrium, QRE），首次将概率化决策引入博弈论：

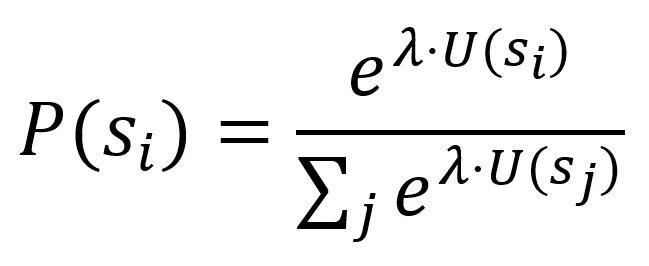
s_i 指的是可以采取的不同行动，U 指的是采取该行动获得的收益。

λ 衡量玩家的理性程度，取非负实数，λ→＋∞ 的时候代表完全理性，λ=0 代表完全不理性。这个公式指的是玩家采取每个行动的概率。这一模型更贴合现实中的“有限理性”行为。

在决策过程中，是否越理性的信息越有利？

答案并非越理性越好。如果你想买股票，想知道股票明天会涨还是会跌。假设存在一个群体能够预测股票涨跌概率，而你无法直接获取这些信息，但该群体会如实告知其买卖意向……你可以挑选一群绝对理性的人或者一群不那么理性的人进行询问（假设知道他们的理性程度，即知道他们的）。

此时如果你问一群绝对理性的人，他们必定告诉你同一个答案，你只能知道涨的概率大还是跌的概率大，因为只要涨的概率大，他们必定全买，跌的概率大，他们必定全卖。而如果你问一群有些理性但是不绝对理性的人，他们都一定概率买，一定概率卖。于是你可以知道他们几个人买，几个人卖，反而可以得到股票涨跌概率的无偏估计。

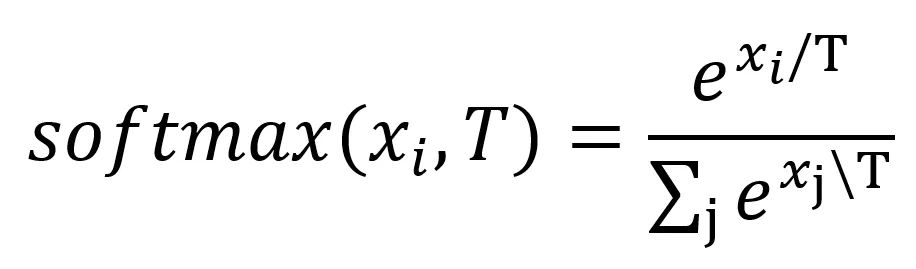
其中 x_i 指的是 Softmax 前每一项的权重，T 是温度。

通过指数变换，Softmax 强调权重大的输出权重仍然大，同时保证输出概率归一化。这一特性使其在分类任务、注意力机制（如 Transformer 模型）中不可或缺。

量子响应均衡在数学形式上与 Softmax 函数高度相似。在 Softmax 里面把 x_i 换成 λ·U(s_i) 就是量子响应均衡了。

从数学的本质上来说，指数函数保证分子分母非负，保证了概率非负，分母的求和操作保证了概率总和是一，满足了归一化。而且两者都可以通过方法来平衡随机性和理性，如量子响应均衡中的 λ 与 Softmax 中的温度 T。

在数学上几乎就是一种东西。但是它们在各自的领域中却有不同的名字。

量子响应均衡中，λ·U(s_i) 结合了收益函数 U（如博弈中的效用）和理性参数 λ，反映决策者对收益的敏感度。

Softmax 中直接用 T 调节温度，并不像经济学一样考虑收益函数。

量子响应均衡的应用

交通博弈：自动驾驶车辆在无信号灯路口需实时协调。QRE 可模拟车辆对通行权的概率化决策，平衡效率与安全。例如，当 λ 较高时，车辆更倾向于“抢行”；λ 较低时则随机礼让，避免僵局。

经济行为建模：在消费者选择模型中，QRE 能解释品牌忠诚度与随机尝试新产品的混合行为，帮助预测市场动态。

Softmax的多应用

大语言模型：通过调整温度参数控制生成文本的创造性。例如，高温度使模型倾向于生成多样但可能不连贯的回答，低温度则输出保守但可靠的答案。

强化学习：在策略梯度方法中，Softmax 用于平衡探索与利用。智能体以一定概率选择非最优动作，避免陷入局部最优。

交叉融合的理论与实践价值

1. 博弈论与深度学习的双向赋能：

逆向思维：将 Softmax 的温度调节机制反向引入 QRE，设计“自适应 λ”算法。例如，在电商定价博弈中，平台根据实时竞争强度自动调整 λ，实现收益最大化。

均衡驱动的神经网络训练：借鉴 QRE 的多智能体均衡思想，改进生成对抗网络（GAN）的训练稳定性，防止模式崩溃（Mode Collapse）。

2. 行为科学与 AI 伦理的交汇：

Softmax 的随机性可模拟人类的认知偏差（如确认偏误），使 AI 助手在提供建议时更具“人情味”。但同时，需警惕过度随机化导致的不可控风险——例如，医疗诊断 AI 若温度（指的是 T，不是气温）过高，会产生噪声，于是可能生成危险建议。当温度过低的时候，总是产生相同的建议而不会生成权重较小的建议，导致漏诊的发生。

文 | 夏一翀

图 | 陈春萌