Published on May 5, 2025 6:56 PM GMT
arXiv | project page | Authors: Yang Yue, Zhiqi Chen, Rui Lu, Andrew Zhao, Zhaokai Wang, Yang Yue, Shiji Song, Gao Huang
This paper from Tsinghua find that RL on verifiable rewards (RLVR) just increases the frequency at which capabilities are sampled, rather than giving a base model new capabilities. To do this, they compare pass@k scores between a base model and an RLed model. Recall that pass@k is the percentage of questions a model can solve at least once given k attempts at each question.
Main result: On a math benchmark, an RLed model (yellow) has much better raw score / pass@1 than the base model (black), but lower pass@256! The authors say that RL prunes away reasoning pathways from the base model, but sometimes reasoning pathways that are rarely sampled end up being useful for solving the problem. So RL “narrows the reasoning boundary”— the region of problems the model is capable of solving sometimes.
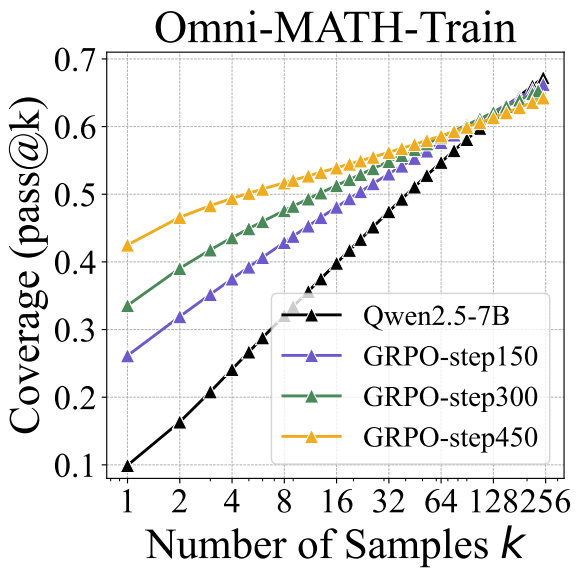
Further results
- Across multiple math benchmarks, base models have higher pass@k than RLed models for sufficiently large k, and sometimes the crossover point is as low as k=4. (Figure 2)Out of domain (i.e. on a different math benchmark) the RLed model does better at pass@256, especially when using algorithms like RLOO and Reinforce++. If there is a crossover point it is in the thousands. (Figure 7)To see if the pass@1024 results are just lucky guesses, they sanity check reasoning traces and find that for most questions, base models generate at least one correct reasoning trace. (But it's unclear whether the majority of correct answers are lucky guesses) Also, for long coding tasks, it's nearly impossible to make a lucky guess.They test the perplexity (Below: Figure 6 left) of the RLed model’s generations (pink bar) relative to the base model. They find it is lower than the base model's perplexity (turquoise bar), which “suggests that the responses from RL-trained models are highly likely to be generated by the base model” conditioned on the task prompt. (Perplexity higher than the base model would imply the RLed model had either new capabilities or higher diversity than the base model.)Distillation from a stronger teacher model, unlike RL, “expands the reasoning boundary”, so performance improves at all best@k values. (Below: Figure 6 right)
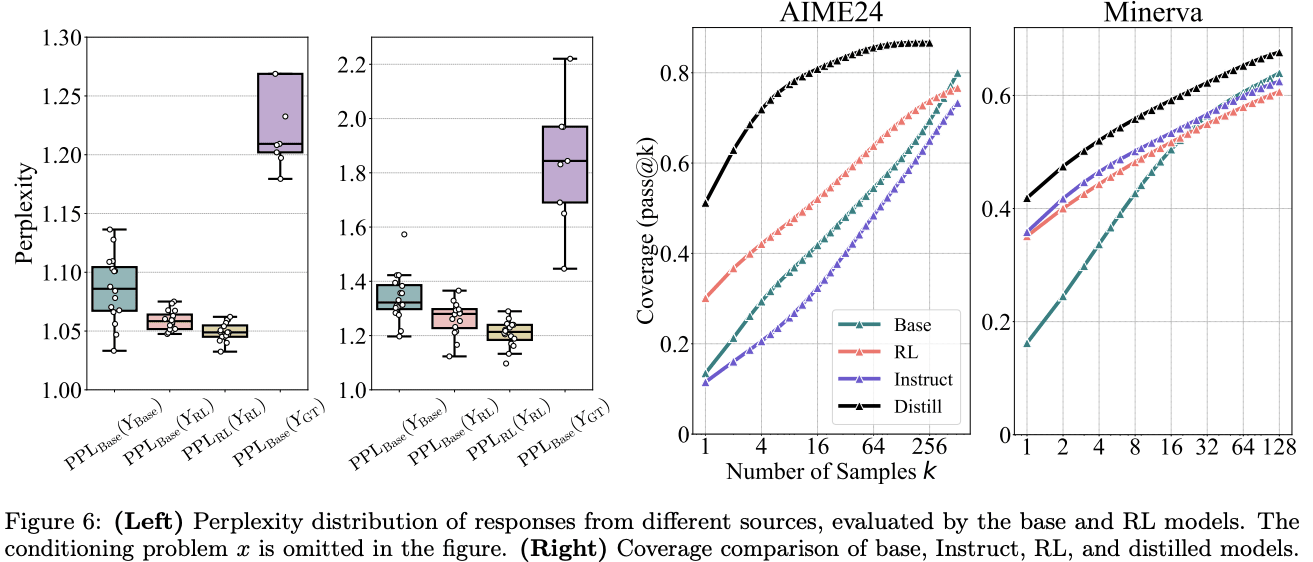
Limitations
- RL can enable emergent capabilities, especially on long-horizon tasks: Suppose that a capability requires 20 correct steps in a row, and the base model has an independent 50% success rate. Then the base model will have a 0.0001% success rate at the overall task and it would be completely impractical to sample 1 million times, but the RLed model may be capable of doing the task reliably.Domains: They only test on math, code generation, and mathematical visual reasoning. It’s plausible that results would be different in domains requiring more creativity.
Takeaways
- This is reminiscent of past work on mode collapse of RLHF.Their methods seem reasonable so I mostly believe this paper modulo the limitations above. The main reason I would disbelieve it is if models frequently have lucky guesses despite their checks-- see point 3 of "further results".Is the recent acceleration in AI software time horizon (doubling time 7 months → 4 months) mainly due to RL, and if so is pass@8 improving slower than pass@1? If so RL could hit diminishing returns. METR already has the data to test how quickly pass@8 is improving, so I could quickly run this and might do so in the comments.
Thanks to @Vladimir_Nesov for mentioning this paper here.
Discuss

