本文介绍了Infra-Bayesianism，一个用于研究人工智能学习的数学框架，它源于Vanessa Kosoy的学习理论AI对齐研究议程。与传统的贝叶斯强化学习不同，Infra-Bayesianism关注的是智能体在无法完全了解真实环境的情况下如何学习和决策。这种“非实现”环境在AI对齐中至关重要，因为它涵盖了智能体将自身视为环境一部分、涉及自我修改、多智能体互动和决策理论问题等场景。文章还探讨了非实现环境对AI对齐研究的重要性，并阐述了贝叶斯主义在非实现环境中的局限性。

🧠Infra-Bayesianism是一种数学框架，用于研究人工智能学习和智能，它解决了智能体在无法完全了解真实环境的情况下进行学习和决策的问题，这与传统的贝叶斯强化学习不同。

⚙️非实现环境在AI对齐中至关重要，因为它涵盖了多种重要场景，包括智能体将自身视为环境一部分、涉及自我修改、多智能体互动以及决策理论问题等。

🤝由于现实世界的复杂性，它本质上是不可实现的。因此，任何关于与物理世界交互的开放世界智能体的理论，如果不解决这个问题，都是不现实的。

🤖自我修改的智能体需要对自身进行建模，但由于自反性，这种模型不可能完美。因此，任何涉及自我修改的场景都是不可实现的。这对于维持AI对齐至关重要，因为智能体可能会学习到一个与基本目标不同的中间优化器。

Published on May 1, 2025 7:06 PM GMT

Introduction 

Infra-Bayesianism is a mathematical framework for studying artificial learning and intelligence that developed from Vanessa Kosoy’s Learning Theoretic AI Alignment Research Agenda. As applied to reinforcement learning, the main character of infra-Bayesianism is an agent that is learning about an unknown environment and making decisions in pursuit of some goal. Infra-Bayesianism provides novel ways to model this agent’s beliefs and make decisions, which address problems arising when an agent does not or cannot consider the true environment possible at the beginning of the learning process. This setting, a non-realizable environment, is relevant to various scenarios important to AI alignment, including scenarios when agents may consider themselves as part of the environment, and scenarios involving self-modifying agents, multi-agent interactions, and decision theory problems. Furthermore, it is the most realistic setting given the computational complexity of the real world.

Here are the links to further posts in this sequence, which continue the introduction given in this post (links will be updated as available):

An Introduction to Reinforcement Learning for Understanding Infra-BayesianismProof Section to an Introduction to Reinforcement Learning for Understanding Infra-BayesianismIntroduction to Credal Sets and Infra-Markov ProcessesProof Section to an Introduction to Credal Sets and Infra-Markov Processes

Non-realizability and irreflexivity

In classical Bayesian reinforcement learning theory, a learning agent starts out with a prior probability distribution over hypotheses called, for brevity, a prior. Each hypothesis describes a possible way that the environment might be, and there is some hypothesis that describes the “true” environment.

The prior expresses the varying credence that the agent puts in each hypothesis ahead of time using prior information. Over time, the agent may rule out hypotheses that must be wrong based on observations. As a result of no-free-lunch theorems (see e.g. Shalev-Shwartz and Shai Ben-David), it is impossible for an agent to consider all environments equally possible in the prior, or even to consider all environments possible in the first place. The agent must start with a set of hypotheses, a hypothesis class, that is smaller than the set of all possible hypotheses.

The goal of the agent is to minimize its loss (or maximize its reward) while under uncertainty about the true environment. A prior over a countable set of hypotheses is said to have a grain of truth if the true hypothesis has non-zero probability in the prior, no matter how small. If a prior has a grain of truth, we are in the realizable setting, which is well-studied in reinforcement learning. For example, Blackwell-Dubin's Merging of Opinions Theorem shows that in the realizable setting, the agent’s predictions will eventually converge to reflect the true environment over time on policy; this means that if the agent continues following the same policy, eventually their predictions will closely match distributions of events that occur.^[1]

Since the true environment is unknown, it is impossible to guarantee realizability when constructing the prior. If the true environment has probability zero in the prior, we say that the prior is misspecified. In this case, an agent's predictions may never converge to reflect the true environment. This is called the misspecified prior problem, and it poses an issue for the goal of proving mathematical statements about how an AI will behave over time in an unknown environment; this is one broad aim of the Learning Theoretic AI Alignment Research Agenda.

For example, suppose an agent is observing an infinite sequence of coin flips, and makes the following assumptions: 1) the outcomes are independent and identically distributed according to some unknown bias of the coin, and 2) all biases are equally likely. The outcome of the next coin flip can be predicted under a Bayesian framework using Laplace's Rule of Succession. This rule states that if $h$ is the total number of observed heads, and $N$ is the total number of observations, then the probability of the next flip yielding heads is $(h+1)/(N+2).$

If the true environment is indeed a biased coin, then in the long run this quantity converges to the true bias of the coin^[2]. In this case, the prior is not misspecified.

If the coin flips are deterministic, yielding heads on even rounds and tails on odd rounds, then the quantity converges to 1/2. While this does not describe the environment precisely, it is the best approximation within the hypothesis class. This is a case where the prior is misspecified, but a reasonable approximation can still be obtained.

On the other hand, suppose the outcomes alternate deterministically in subsequences of length $2^k$ for $k=0,1,2,\dots$, meaning there is 1 head, followed by 2 tails, followed by 4 heads, followed by 8 tails, and so on. The prior is again misspecified in this case. As shown in Figure 1, at the end of each subsequence, a probability close to $2/3$ is assigned to the outcome that never appears in the next subsequence. The prediction is corrected slowly and is wrong for a longer period of time for each subsequence. In this case, Laplace's Rule of Succession never yields a good approximation to the true environment.

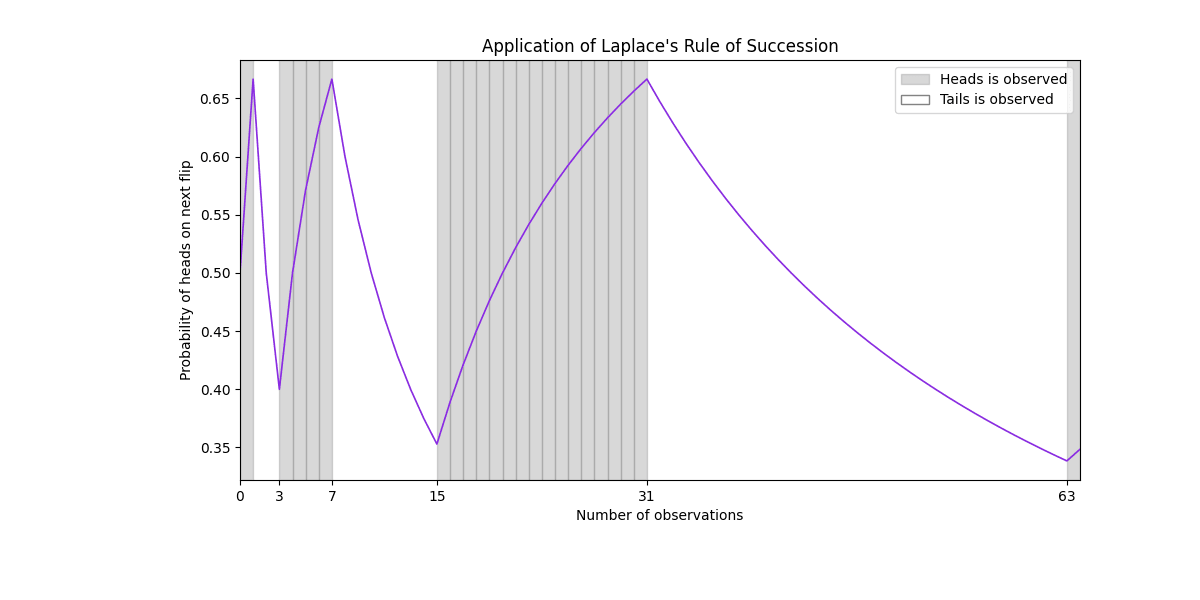
Not only is realizability not guaranteed, it is extremely unrealistic because of the computational complexity of the real world. Furthermore, it is impossible for an agent to specify a hypothesis that has greater computational complexity than itself, which is the problem of irreflexivity. The fact that all hypotheses specified in the prior of a Bayesian agent are computable with low computational complexity is what Vanessa was referring to when she said on the AXRP podcast,

“Bayesian agents have a dogmatic belief that the world has low computational complexity. They believe this fact with probability one, because all their hypotheses have low computational complexity. You’re assigning probability one to this fact, and this is a wrong fact, and when you’re assigning probability one to something wrong, then it’s not surprising you run into trouble, right?”

On the other hand, infra-Bayesian agents do not have this dogmatic belief, as their hypotheses allow them to capture the belief that parts of the world might have high computational complexity or are incomputable. We’ll explore an example of this in the section on Dutch Booking Bayesians. First, we’ll elaborate on why having a theory of reinforcement learning for non-realizable environments is relevant to AI alignment.

The significance of non-realizability for AI alignment research

In this section, we describe (non-exhaustively) several scenarios relevant to AI alignment that are non-realizable.

1) The real world as an environment:

Due to its complexity, the real world is non-realizable. Therefore, any theory of open-world agents that interact with the physical world is unrealistic if it does not address this.

2) Environments that don’t assume Cartesian duality:

An AI is ultimately running on hardware that is part of the environment, and thus can be influenced by forces in the environment. For example, the AI’s source code could be modified by external forces or by itself in the case of self-modification. Therefore, it is unrealistic to assume that the AI is not part of the environment.

If an AI is considered a part of the environment it is trying to learn about, the environment therefore has greater computational complexity than itself. Due to irreflexivity, the AI cannot perfectly model these types of environments. Therefore, if Cartesian duality is not assumed, this setting is unrealizable.

3) Self-modifying agents:

In order for an agent to self-modify (including to self-improve), it must have some model of itself. Due to irreflexivity, it is not possible for this model to be perfect, and thus any setting involving self-modification is unrealizable.

This is significant because one problem in AI alignment is the problem of sustaining alignment as an agent evolves. For example, as described in Risks from Learned Optimization, a learning agent may learn a mesa-optimizer that has a mesa-objective that is different from the base-objective. An agent could also create a successor agent with greater intelligence, introducing the problem of robust delegation, or create multiple sub-agents, introducing the problem of subsystem alignment (see e.g. Embedded World Models). 

4) Multi-agent interactions and Newcomb-like decision theory problems:

As various agents interact, it is natural for them to build models of the other agents. Due to irreflexivity, all of their models cannot be perfect. For example, if an agent Omega has a perfect model of Bob, then Bob cannot have a perfect model of Omega, for otherwise Bob would have a perfect model of themselves.

Omega is the key character of the Dutch-Booking Bayesians thought experiment, described below, and various problems from decision theory called Newcomb-like problems. Decision theory is the study of how agents trying to achieve some goal, instrumentally rational agents, "should" behave, which is a relevant aspect of ensuring that an AI makes “good” decisions across a range of scenarios, including situations which may be very different from training scenarios. In particular, one goal of AI alignment may include identifying an “ideal” decision theory that can be implemented by an AI, a problem described in detail in Towards Idealized Decision Theory.

Dutch Booking Bayesians: Why Bayesianism is Inadequate

The thought experiment of Dutch-Booking Bayesians aims to explain the shortcomings of Bayesianism in an environment that is non-realizable. We will use a simple example to demonstrate the more general principle.

Let $A$ and $B$ denote yes-no questions, each having probability 1/2 of the answer being yes. An agent Omega will choose whether to ask the question $A$ or $B$. The second agent can then bet yes, bet no, or refuse to bet. If correct, the agent gains $1.1 and if incorrect, they lose $1. Importantly, Omega is a powerful agent with good prediction powers about the questions and how their opponent will answer them. 

Suppose that Omega's opponent is Bob, a Bayesian agent. Bob has a joint probability distribution over the truth values of the questions and whether Omega chooses $A$ or $B$. For simplicity, assume that the marginal distribution on the truth values is a uniform distribution. A normal causality assumption postulates that the answer chosen by Bob does not influence the real answer. Since the bet appears fair, Bob will choose to bet.

However, Bob only has probability $1/4$ of being correct on both $A$ and $B$. This allows for Omega to give Bob a question in which they will be wrong with probability $3/4$. Therefore, the expected payoff in one round of choosing to bet is $1/4\cdot 1.1+3/4\cdot (-1)=-0.475<0.$

This scenario is a Dutch book against Bob, a series of bets that appear fair ahead of time, but that result in guaranteed or “sure” net loss for Bob. Another way of framing this thought experiment is that Bob must either drop the causality assumption, thereby postulating an odd causal structure about the world, or be Dutch-booked.

How does infra-Bayesianism save our other character, Ingrid, from such a Dutch book? Infra-Bayesian Ingrid's hypothesis about the environment is a set of probability distributions rather than a single probability distribution. In particular, Ingrid's belief is captured by a set containing all probability distributions of the form that Bob considered rather than choosing just one. This is an example of a credal set, which is defined and discussed further in the next post in this sequence.

For Ingrid, expected payoff is calculated as the worst case expected payoff over the credal set. For example, the following distribution is a valid member of the credal set.

Probability 1/4: $A$ - yes, $B$ - yes, Omega - $A$ 
Probability 1/4: $A$ - yes, $B$ - no, Omega - $B$ 
Probability 1/4: $A$ - no, $B$ - yes, Omega - $A$ 
Probability 1/4: $A$ - no, $B$ - no, Omega - $A$ 

If Ingrid were to bet yes on both questions, then the expected payoff under this distribution is $-\mathrm{0.475.}$This example generalizes: For any choice of bets, there is a distribution in the credal set specifying a question selection by Omega that gives negative expected payoff. Therefore, by defining the expected payoff over the set to be the worst case for any element, choosing to bet always has negative expected payoff. 

On the other hand, refusing to bet has an expected payoff of zero for all distributions in the credal set. Therefore, Ingrid can use the paradigm of infra-Bayesianism to systematically refuse the bets offered by Omega and escape the Dutch book. So, infra-Bayesianism is not only an epistemic theory that helps Ingrid quantify their belief under uncertainty, but it also prescribes a decision rule that helps Ingrid decide what to do with it.

Acknowledgements 

This work was initially commissioned by MIRI, and then continued in CORAL. I am grateful to Vanessa Kosoy for her valuable comments and suggestions, including the mathematical examples, and to Hannah Gabor and Changyan Wang, whose comments helped improve the writing and clarity of ideas.

1. ^{^}

   On the other hand, an agent might still hold incorrect beliefs about counterfactuals, observations or events that could have been possible if they had changed policy.

2. ^{^}

   By the Strong Law of Large Numbers.

3. ^{^}

   Technically speaking: Any given measurable event.

Discuss