$中远海控(SH601919)$ $中远海控(01919)$
前几天@HIS1963 大哥说自己用小学生的方法计算了CCFI与海控业绩及股息率的关系网页链接
今天我尝试用大学生的方法计算CCFI与海控季度盈利之间的关系,目的是得到预测方程,以便通过CCFI预测海控每季度的盈利。
废话不多先上结论:
1.通过直线回归的方法获得了回归方程:
Y=0.12X-77
季度盈利=0.12×当季CCFI均值-77(单位:亿元)
意味着CCFI每变化100点,季度盈利相应变化12亿(±2亿),年化48亿。
2.由于公司资产质量的飞跃和经营能力的提高,此算式可能会低估盈利水平
3.CCFI与当季盈利相关程度非常高,相关系数高达0.95(最大值是1.0)
4.CCFI处于极小值(1000以下)或者极大值(3000以上)时,此算式预测的盈利与实际值之间可能会出现较大偏差。原因是显而易见的,运价处于极值的时候,公司很可能会在会计规则内调整业绩。
下面是统计学推导过程,不感兴趣的朋友可以直接跳到应用示例部分。
在统计学上要研究两个相关变量之间的关系,通过一个变量预测另一个变量,最经典的方法是通过既往历史前值拟合出线性回归方程。线性回归有多种形态,其中最简单的形态是直线回归。我们需要先画出散点图,观察前值分布是否符合直线回归,再进行拟合计算。如果散点图不呈现线性关系,则不能做线性回归。
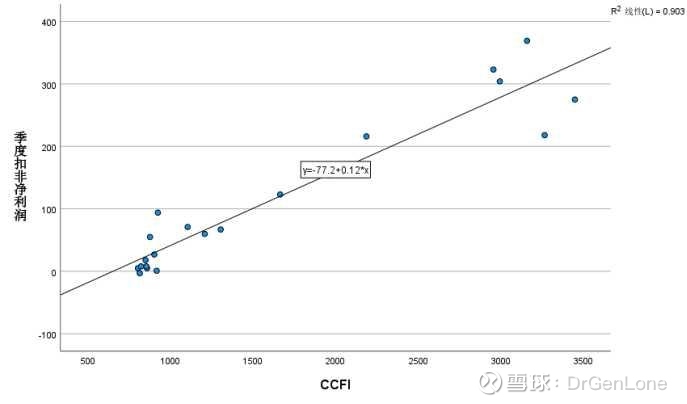
回归分析用的是统计学软件SPSS,数据来源于@今宵韭醒何处 兄弟做的总结表格,感谢!
1. 画散点图,将自变量CCFI(X)放入X轴;将因变量季度盈利(Y)放入Y轴,其它默认。结果见图一,初步目测还是比较符合直线分布的。但是在CCFI较小和较大值,也就是两端,分布比较分散。
2. 菜单选择分析-回归-线性,确定后秒出结果
3. 结果解读(图二对应红字):

A. R (0.95)是两者相关系数,CCFI与当季盈利相关程度非常高。
B. 斜率0.119,是方程中最关键的系数k,Constant(回归方程的截距)是方程中的常数项b,负的77
C. 斜率的95%置信区间,你可以理解为斜率可能的高低值(0.1-0.137),如果你觉得方程可能低估了盈利,那把0.12替换为0.14,算出来预测盈利就会高很多。相反你就取0.1
其他一些统计检验都是对上述数值的有效性进行检验,结果显示无论是直线关系还是斜率、常数项都是有统计学意义的。
因此,建立回归方程 Y=0.12X - 77,X为CCFI,Y为当季盈利。
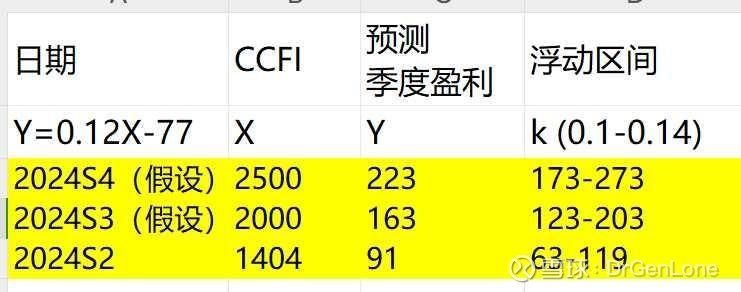
应用示例见图三:在电子表格软件中建立本方程式,输入今年第二季度CCFI均值以及第三、第四季度模拟均值(仅用于示范,不可当真),可得出相应季度预测盈利,以及可能的取值区间。
本研究局限性:
1. 采纳数据时间跨度较大,涵盖了海控暴富前后,但资产质量的改善会显著提升盈利能力;另一方面由于公司减少了中间环节蚕食利润,拓展了上下游供应链业务,相比21.22年盈利能力更强。因此本方程大概率会低估盈利约10-20%
2. 当运价处于极低或极高值时,公司可能会调整业绩,从而产生较大不确定性,因此本方程最适用于CCFI在1000-3000之间的范围内。
3. 采纳的样本量为20个,不算少但也不算很多,后续期望能纳入更多的业绩数据以改善本方程预测准确度。
4. 本研究仅限于预测季度盈利,由于全年运价波动性较大,不宜直接×4用于预测年度盈利(但可以做梦)。
全文结论
本文通过线性回归的方法获得了海控季度业绩的预测方程式,主要结果显示当季度平均CCFI每提升100点,季度盈利相应提升约12亿(潜在区间10-14亿)。在应用本方程进行预测时,需要注意应用范围及潜在风险。欢迎各路统计学大神指点,进一步完善。
后记:由于运费的延迟结算,也有人认为当季CCFI的变化可能更多地反映在海控的下一季盈利中。因此我们也计算了当季CCFI与下季盈利之间的相关性,相关系数为0.88,低于当季盈利的相关系数(0.95)。据此可以认为与当季盈利相关程度更高。
本话题在雪球有63条讨论,点击查看。
雪球是一个投资者的社交网络,聪明的投资者都在这里。
点击下载雪球手机客户端 http://xueqiu.com/xz]]>

